Draw a field

The objective here is to create and manipulate a field. A field is the agregation of a mesh of a domain and a sample of values in associated to each vertex of the mesh.

We note the vertices of and the associated values in .

A field is stored in the Field object that stores the mesh and the values at each vertex of the mesh. It can be built from a mesh and values or as a realization of a stochastic process.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

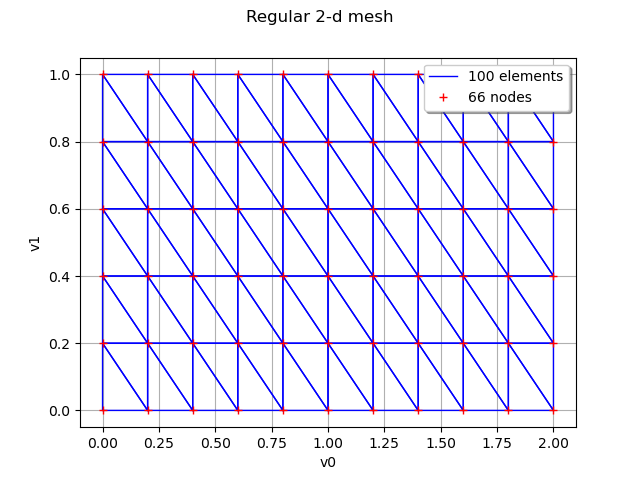
First, define a regular 2-d mesh

discretization = [10, 5]
mesher = ot.IntervalMesher(discretization)
lowerBound = [0.0, 0.0]
upperBound = [2.0, 1.0]
interval = ot.Interval(lowerBound, upperBound)
mesh = mesher.build(interval)
graph = mesh.draw()
graph.setTitle("Regular 2-d mesh")
view = viewer.View(graph)

Create a field as a realization of a process

amplitude = [1.0]
scale = [0.2] * 2
myCovModel = ot.ExponentialModel(scale, amplitude)
myProcess = ot.GaussianProcess(myCovModel, mesh)
field = myProcess.getRealization()

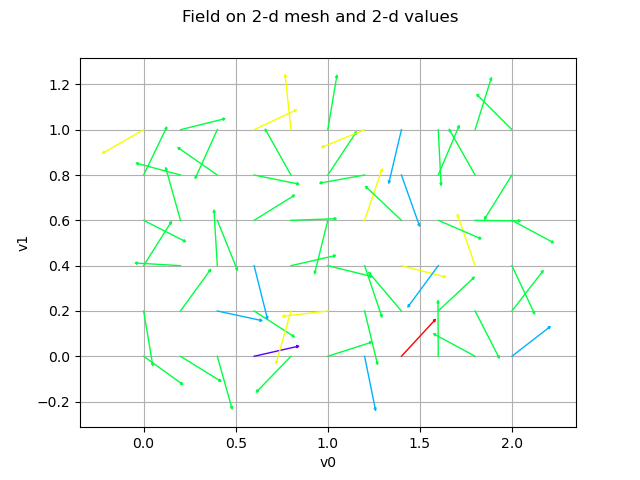
Create a field from a mesh and some values

values = ot.Normal([0.0] * 2, [1.0] * 2, ot.CorrelationMatrix(2)).getSample(
    len(mesh.getVertices())
)
for i in range(len(values)):
    x = values[i]
    values[i] = 0.05 * x / x.norm()
field = ot.Field(mesh, values)
graph = field.draw()
graph.setTitle("Field on 2-d mesh and 2-d values")
view = viewer.View(graph)

Compute the input mean of the field

field.getInputMean()

[0.0132072,0.00100751]

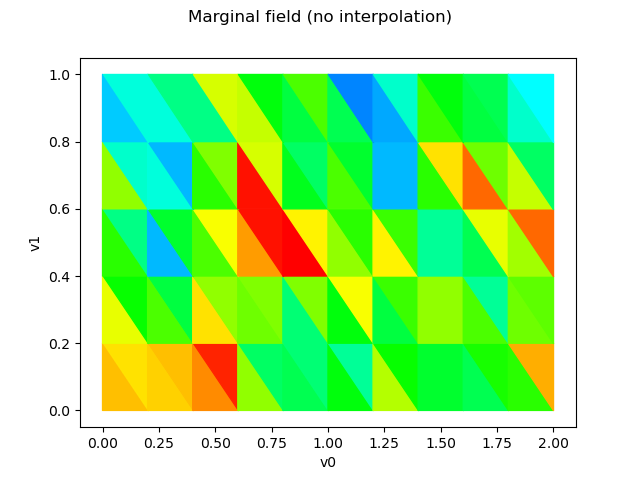
Draw the field without interpolation

graph = field.drawMarginal(0, False)
graph.setTitle("Marginal field (no interpolation)")
view = viewer.View(graph)

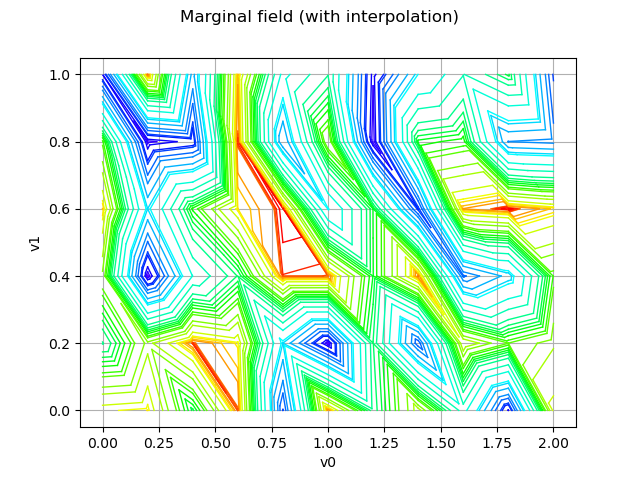
Draw the field with interpolation

graph = field.drawMarginal(0)
graph.setTitle("Marginal field (with interpolation)")
view = viewer.View(graph)

Deform the mesh from the field according to the values of the field The dimension of the mesh (ie of its vertices) must be the same as the dimension of the field (ie its values)

graph = field.asDeformedMesh().draw()
graph.setTitle("Deformed 2-d mesh")
view = viewer.View(graph)

Export to the VTK format

field.exportToVTKFile("field.vtk")
with open("field.vtk") as f:
    print(f.read()[:100])

plt.show()

# vtk DataFile Version 3.0
Unnamed
ASCII

DATASET UNSTRUCTURED_GRID
POINTS 66 float
0 0 0.0
0.2 0 0.