The cantilever beam model¶
We are interested in the vertical deviation of a diving board created by a child diver. We consider a child whose weight generates a force approximately equal to 300N (i.e. almost 30 kg). Because of the uncertainties in the weight of the person, we consider that the force is a random variable. The length of the diving board is between 2.5 m and 2.6 m. The Young modulus is uncertain and between 65 and 75 GPa, which corresponds to the fiberglass material, a material often used for diving boards. Uncertainties in the production of the material are taken into account in the Young modulus and the section modulus of the board.
We consider a cantilever beam defined by its Young’s modulus , its length
and its section modulus
.
One end of the cantilever beam is built in a wall and we apply a concentrated bending load
at the other end of the beam, resulting in a deviation
.
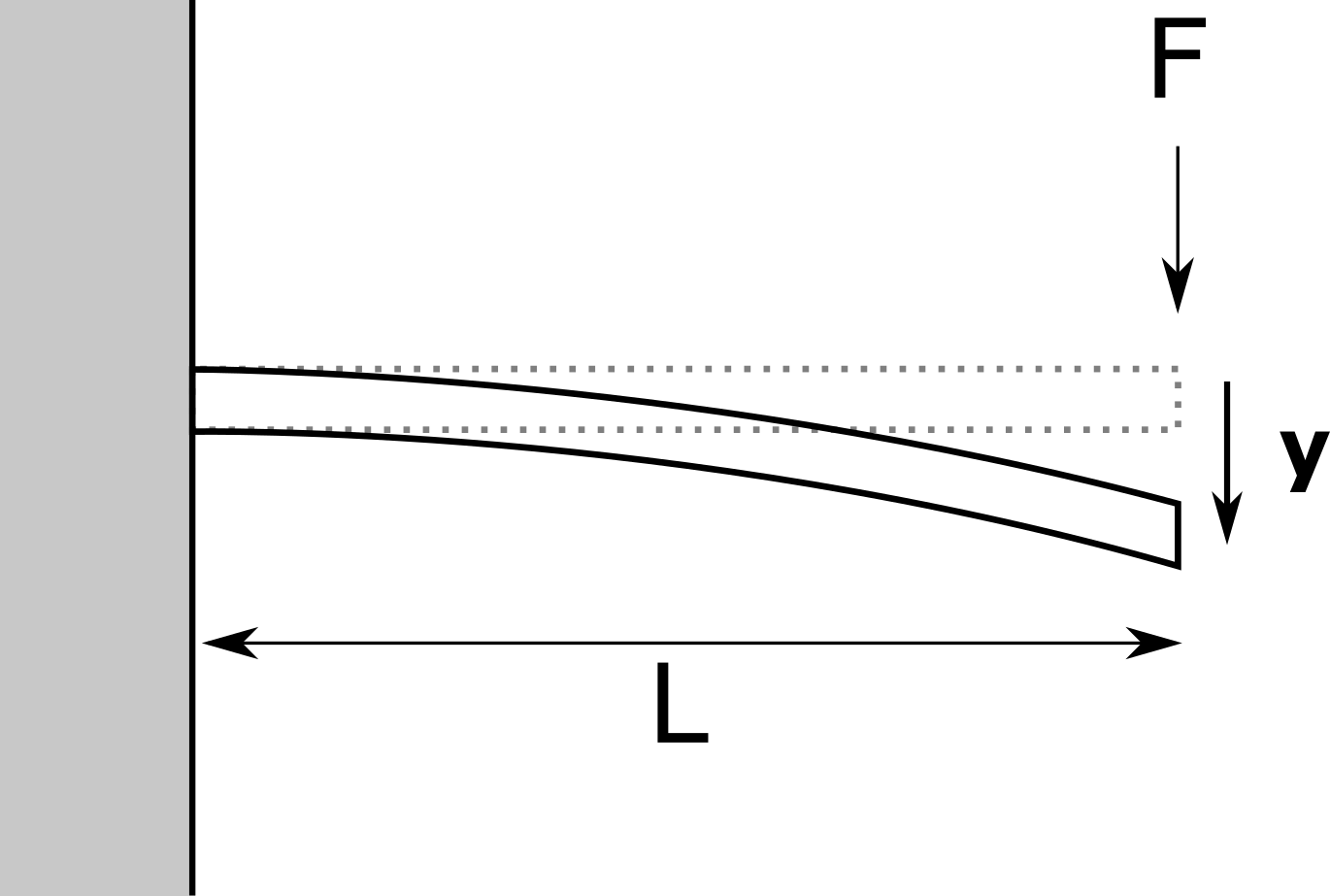
The beam geometry¶
Inputs
: Young modulus (Pa), Beta(
,
, a =
,
)
: Loading (N), Lognormal(
,
, shift=0.0)
: Length of beam (m), Uniform(min=2.5, max= 2.6)
: Moment of inertia (
), Beta(
,
,
,
).
In the previous table and
are the mean and the standard deviation of
.
- We assume that the random variables E, F, L and I are dependent and associated with a gaussian copula which correlation matrix is :
In other words, we consider that the variables L and I are negatively correlated : when the length L increases, the moment of intertia I decreases.
Output
- The vertical displacement at free end of the cantilever beam is:
- A typical event of interest is when the beam deviation is too large which is a failure :
Load the use case¶
We can load this classical model from the use cases module as follows :
>>> from openturns.usecases import cantilever_beam
>>> # Load the cantilever beam example
>>> cb = cantilever_beam.CantileverBeam()
API documentation¶
See CantileverBeam.
 OpenTURNS
OpenTURNS