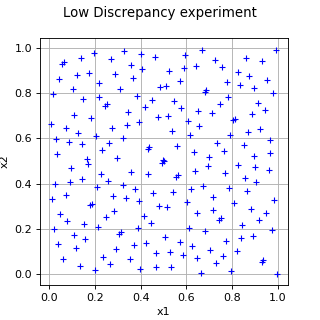
LowDiscrepancyExperiment¶

(Source code, png, hires.png, pdf)

class LowDiscrepancyExperiment(*args)¶

LowDiscrepancy experiment.

Available constructors:

LowDiscrepancyExperiment(size, restart)

LowDiscrepancyExperiment(sequence, size, restart)

LowDiscrepancyExperiment(sequence, distribution, size, restart)

Parameters:

sizepositive int: Number $N$ of points of the sequence.
sequenceLowDiscrepancySequence: Sequence of points $(u_1, \cdots, u_N)$ with low discrepancy. If not specified, the sequence is a SobolSequence.
distributionDistribution: Distribution $\mu$ of dimension $n$ . The low discrepancy sequence $(u_1, \cdots, u_N)$ is uniformly distributed over $[0,1]^n$ . We use an iso-probabilistic transformation from the independent copula of dimension $n$ to the given distribution. The weights are all equal to $1/N$ .
restartbool: Flag to tell if the low discrepancy sequence must be restarted from its initial state at each change of distribution or not. Default is True: the sequence is restarted at each change of distribution.

See also

WeightedExperiment

Notes

The generate() method generates points $(\Xi_i)_{i \in I}$ according to the distribution $\mu$ . When the generate() method is called again, the generated sample changes. In case of dependent marginals, the approach based on [cambou2017] is used.

Examples

>>> import openturns as ot
>>> distribution = ot.ComposedDistribution([ot.Uniform(0.0, 1.0)] * 2)

Generate the sample with a reinitialization of the sequence at each change of distribution:

>>> experiment = ot.LowDiscrepancyExperiment(ot.SobolSequence(), distribution, 5, True)
>>> print(experiment.generate())
    [ y0    y1    ]
0 : [ 0.5   0.5   ]
1 : [ 0.75  0.25  ]
2 : [ 0.25  0.75  ]
3 : [ 0.375 0.375 ]
4 : [ 0.875 0.875 ]
>>> print(experiment.generate())
    [ y0     y1     ]
0 : [ 0.625  0.125  ]
1 : [ 0.125  0.625  ]
2 : [ 0.1875 0.3125 ]
3 : [ 0.6875 0.8125 ]
4 : [ 0.9375 0.0625 ]
>>> experiment.setDistribution(distribution)
>>> print(experiment.generate())
    [ y0    y1    ]
0 : [ 0.5   0.5   ]
1 : [ 0.75  0.25  ]
2 : [ 0.25  0.75  ]
3 : [ 0.375 0.375 ]
4 : [ 0.875 0.875 ]

Generate the sample keeping the previous state of the sequence at each change of distribution:

>>> experiment = ot.LowDiscrepancyExperiment(ot.SobolSequence(), distribution, 5, False)
>>> print(experiment.generate())
    [ y0    y1    ]
0 : [ 0.5   0.5   ]
1 : [ 0.75  0.25  ]
2 : [ 0.25  0.75  ]
3 : [ 0.375 0.375 ]
4 : [ 0.875 0.875 ]
>>> print(experiment.generate())
    [ y0     y1     ]
0 : [ 0.625  0.125  ]
1 : [ 0.125  0.625  ]
2 : [ 0.1875 0.3125 ]
3 : [ 0.6875 0.8125 ]
4 : [ 0.9375 0.0625 ]
>>> experiment.setDistribution(distribution)
>>> print(experiment.generate())
    [ y0     y1     ]
0 : [ 0.4375 0.5625 ]
1 : [ 0.3125 0.1875 ]
2 : [ 0.8125 0.6875 ]
3 : [ 0.5625 0.4375 ]
4 : [ 0.0625 0.9375 ]

Generate a sample according to a distribution with dependent marginals:

>>> distribution = ot.Normal([0.0]*2, ot.CovarianceMatrix(2, [4.0, 1.0, 1.0, 9.0]))
>>> experiment = ot.LowDiscrepancyExperiment(ot.SobolSequence(), distribution, 5, False)
>>> print(experiment.generate())
    [ y0        y1        ]
0 : [  0         0        ]
1 : [  1.34898  -1.65792  ]
2 : [ -1.34898   1.65792  ]
3 : [ -0.637279 -1.10187  ]
4 : [  2.3007    3.97795  ]

Methods

`generate`()	Generate points according to the type of the experiment.
`generateWithWeights`()	Generate points and their associated weight according to the type of the experiment.
`getClassName`()	Accessor to the object's name.
`getDistribution`()	Accessor to the distribution.
`getId`()	Accessor to the object's id.
`getName`()	Accessor to the object's name.
`getRandomize`()	Return the value of the randomize flag.
`getRestart`()	Return the value of the restart flag.
`getSequence`()	Return the sequence.
`getShadowedId`()	Accessor to the object's shadowed id.
`getSize`()	Accessor to the size of the generated sample.
`getVisibility`()	Accessor to the object's visibility state.
`hasName`()	Test if the object is named.
`hasUniformWeights`()	Ask whether the experiment has uniform weights.
`hasVisibleName`()	Test if the object has a distinguishable name.
`setDistribution`(distribution)	Accessor to the distribution.
`setName`(name)	Accessor to the object's name.
`setRandomize`(randomize)	Set the value of the randomize flag.
`setRestart`(restart)	Set the value of the restart flag.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setSize`(size)	Accessor to the size of the generated sample.
`setVisibility`(visible)	Accessor to the object's visibility state.

__init__(*args)¶

generate()¶

Generate points according to the type of the experiment.

Returns:

sampleSample: Points $(\Xi_i)_{i \in I}$ which constitute the design of experiments with $card I = size$ . The sampling method is defined by the nature of the weighted experiment.

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5)
>>> sample = myExperiment.generate()
>>> print(sample)
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]
3 : [ -0.355007  1.43725  ]
4 : [  0.810668  0.793156 ]

generateWithWeights()¶

Generate points and their associated weight according to the type of the experiment.

Returns:

sampleSample: The points which constitute the design of experiments. The sampling method is defined by the nature of the experiment.
weightsPoint of size $cardI$: Weights $(\omega_i)_{i \in I}$ associated with the points. By default, all the weights are equal to $1/cardI$ .

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5)
>>> sample, weights = myExperiment.generateWithWeights()
>>> print(sample)
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]
3 : [ -0.355007  1.43725  ]
4 : [  0.810668  0.793156 ]
>>> print(weights)
[0.2,0.2,0.2,0.2,0.2]

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDistribution()¶

Accessor to the distribution.

Returns:

distributionDistribution: Distribution used to generate the set of input data.

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getRandomize()¶

Return the value of the randomize flag.

Returns:

randomizebool: The value of the randomize flag.

getRestart()¶

Return the value of the restart flag.

Returns:

restartbool: The value of the restart flag.

getSequence()¶

Return the sequence.

Returns:

sequenceLowDiscrepancySequence: Sequence of points $(u_1, \cdots, u_N)$ with low discrepancy.

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getSize()¶

Accessor to the size of the generated sample.

Returns:

sizepositive int: Number $cardI$ of points constituting the design of experiments.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasUniformWeights()¶

Ask whether the experiment has uniform weights.

Returns:

hasUniformWeightsbool: Whether the experiment has uniform weights.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

setDistribution(distribution)¶

Accessor to the distribution.

Parameters:

distributionDistribution: Distribution used to generate the set of input data.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setRandomize(randomize)¶

Set the value of the randomize flag.

Parameters:

randomizebool: Use a cyclic scrambling of the low discrepancy sequence, it means, the whole low discrepancy sequence is translated by a random vector modulo 1. See [lecuyer2005] for the interest of such a scrambling. Default is False.

setRestart(restart)¶

Set the value of the restart flag.

Parameters:

restartbool: The value of the restart flag. If equals to True, the low discrepancy sequence is restarted at each change of distribution, else it is changed only if the new distribution has a dimension different from the current one.

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters: