Pagmo¶

class Pagmo(*args)¶

Pagmo algorithms.

This class exposes bio-inspired and evolutionary global optimization algorithms from the Pagmo library. These algorithms start from an initial population and make it evolve to obtain a final population after a defined number of generations (by setGenerationNumber()). A few of these algorithms allow for multi-objective optimization, and in that case the result is not the best point among the final population but a set of dominant points: a pareto front.

Parameters:

problemOptimizationProblem: Optimization problem to solve
algoNamestr, default=’gaco’: Identifier of the optimization method to use.
startingSample2-d sequence of float, optional: Initial population

Notes

Starting points provided through the startingSample parameter should be within the bounds of the OptimizationProblem, but this is not enforced.

Pagmo provides the following global heuristics:

Algorithm	Description	Multi-objective	MINLP	Batch
gaco	Extended Ant Colony Optimization	no	yes	yes
de	Differential Evolution	no	no	no
sade	Self-adaptive DE (jDE and iDE)	no	no	no
de1220	Self-adaptive DE (de_1220 aka pDE)	no	no	no
gwo	Grey wolf optimizer	no	no	no
ihs	Improved Harmony Search	no	yes	no
pso	Particle Swarm Optimization	no	no	no
pso_gen	Particle Swarm Optimization Generational	no	no	yes
sea	(N+1)-ES Simple Evolutionary Algorithm	no	no	no
sga	Simple Genetic Algorithm	no	yes	no
simulated_annealing	Corana’s Simulated Annealing	no	no	no
bee_colony	Artificial Bee Colony	no	no	no
cmaes	Covariance Matrix Adaptation Evo. Strategy	no	no	no
xnes	Exponential Evolution Strategies	no	no	no
nsga2	Non-dominated Sorting GA	yes	yes	yes
moead	Multi-objective EA vith Decomposition	yes	no	no
mhaco	Multi-objective Hypervolume-based ACO	yes	yes	yes
nspso	Non-dominated Sorting PSO	yes	no	yes

Only gaco and ihs natively support constraints, but for the other algorithms constraints are emulated through penalization. For mhaco, the initial population must satisfy constraints, else it is built by boostrap on valid points with the same population size as the one provided. Some algorithms support batch evaluation, except when constraints are emulated, see setBlockSize(). Default parameters are available in the ResourceMap for each algorithm, refer to the correspondings keys in the Pagmo documentation.

Examples

Define an optimization problem to find the minimum of the Rosenbrock function:

>>> import openturns as ot
>>> dim = 2
>>> rosenbrock = ot.SymbolicFunction(['x1', 'x2'], ['(1-x1)^2+100*(x2-x1^2)^2'])
>>> bounds = ot.Interval([-5.0] * dim, [5.0] * dim)
>>> problem = ot.OptimizationProblem(rosenbrock)
>>> problem.setBounds(bounds)

Sample the initial population inside a box:

>>> uniform = ot.ComposedDistribution([ot.Uniform(-2.0, 2.0)] * dim)
>>> ot.RandomGenerator.SetSeed(0)
>>> init_pop = uniform.getSample(5)

Run GACO on our problem:

>>> algo = ot.Pagmo(problem, 'gaco', init_pop)
>>> algo.setGenerationNumber(5)
>>> algo.run() 
>>> result = algo.getResult() 
>>> x_star = result.getOptimalPoint() 
>>> y_star = result.getOptimalValue() 

Get the final population:

>>> final_pop_x = result.getFinalPoints() 
>>> final_pop_y = result.getFinalValues() 

Define a multi-objective problem:

>>> dim = 2
>>> model = ot.SymbolicFunction(['x', 'y'], ['x^2+y^2*(1-x)^3', '-x^2'])
>>> bounds = ot.Interval([-2.0] * dim, [3.0] * dim)
>>> problem = ot.OptimizationProblem(model)
>>> problem.setBounds(bounds)

Sample the initial population inside a box:

>>> uniform = ot.ComposedDistribution([ot.Uniform(-2.0, 3.0)] * dim)
>>> ot.RandomGenerator.SetSeed(0)
>>> init_pop = uniform.getSample(5)

Run NSGA2 on our problem:

>>> algo = ot.Pagmo(problem, 'nsga2', init_pop)
>>> algo.setGenerationNumber(5)
>>> algo.run() 
>>> result = algo.getResult() 
>>> final_pop_x = result.getFinalPoints() 
>>> final_pop_y = result.getFinalValues() 

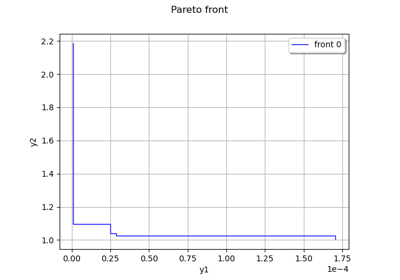
Get the best front points and values:

>>> front0 = result.getParetoFrontsIndices()[0] 
>>> front0_x = final_pop_x.select(front0) 
>>> front0_y = final_pop_y.select(front0) 

Methods

`GetAlgorithmNames`()	Accessor to the list of algorithm names provided.
`getAlgorithmName`()	Accessor to the algorithm name.
`getBlockSize`()	Block size accessor.
`getClassName`()	Accessor to the object's name.
`getGenerationNumber`()	Generation number accessor.
`getId`()	Accessor to the object's id.
`getMaximumAbsoluteError`()	Accessor to maximum allowed absolute error.
`getMaximumConstraintError`()	Accessor to maximum allowed constraint error.
`getMaximumEvaluationNumber`()	Accessor to maximum allowed number of evaluations.
`getMaximumIterationNumber`()	Accessor to maximum allowed number of iterations.
`getMaximumRelativeError`()	Accessor to maximum allowed relative error.
`getMaximumResidualError`()	Accessor to maximum allowed residual error.
`getName`()	Accessor to the object's name.
`getProblem`()	Accessor to optimization problem.
`getResult`()	Accessor to optimization result.
`getSeed`()	Random generator seed accessor.
`getShadowedId`()	Accessor to the object's shadowed id.
`getStartingPoint`()	Accessor to starting point.
`getStartingSample`()	Accessor to the sample of starting points.
`getVerbose`()	Accessor to the verbosity flag.
`getVisibility`()	Accessor to the object's visibility state.
`hasName`()	Test if the object is named.
`hasVisibleName`()	Test if the object has a distinguishable name.
`run`()	Launch the optimization.
`setAlgorithmName`(algoName)	Accessor to the algorithm name.
`setBlockSize`(blockSize)	Block size accessor.
`setGenerationNumber`(generationNumber)	Generation number accessor.
`setMaximumAbsoluteError`(maximumAbsoluteError)	Accessor to maximum allowed absolute error.
`setMaximumConstraintError`(maximumConstraintError)	Accessor to maximum allowed constraint error.
`setMaximumEvaluationNumber`(...)	Accessor to maximum allowed number of evaluations.
`setMaximumIterationNumber`(maximumIterationNumber)	Accessor to maximum allowed number of iterations.
`setMaximumRelativeError`(maximumRelativeError)	Accessor to maximum allowed relative error.
`setMaximumResidualError`(maximumResidualError)	Accessor to maximum allowed residual error.
`setName`(name)	Accessor to the object's name.
`setProblem`(problem)	Accessor to optimization problem.
`setProgressCallback`(*args)	Set up a progress callback.
`setResult`(result)	Accessor to optimization result.
`setSeed`(seed)	Random generator seed accessor.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setStartingPoint`(point)	Accessor to starting point.
`setStartingSample`(startingSample)	Accessor to the sample of starting points.
`setStopCallback`(*args)	Set up a stop callback.
`setVerbose`(verbose)	Accessor to the verbosity flag.
`setVisibility`(visible)	Accessor to the object's visibility state.

__init__(*args)¶

static GetAlgorithmNames()¶

Accessor to the list of algorithm names provided.

Returns:

namesDescription: List of algorithm names provided, according to its naming convention.

getAlgorithmName()¶

Accessor to the algorithm name.

Returns:

algoNamestr: The identifier of the algorithm.

getBlockSize()¶

Block size accessor.

Returns:

blockSizeint: Batch evaluation granularity.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getGenerationNumber()¶

Generation number accessor.

Returns:

genint: Number of generations to evolve.

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getMaximumAbsoluteError()¶

Accessor to maximum allowed absolute error.

Returns:

maximumAbsoluteErrorfloat: Maximum allowed absolute error, where the absolute error is defined by $\epsilon^a_n=\|\vect{x}_{n+1}-\vect{x}_n\|_{\infty}$ where $\vect{x}_{n+1}$ and $\vect{x}_n$ are two consecutive approximations of the optimum.

getMaximumConstraintError()¶

Accessor to maximum allowed constraint error.

Returns:

maximumConstraintErrorfloat: Maximum allowed constraint error, where the constraint error is defined by $\gamma_n=\|g(\vect{x}_n)\|_{\infty}$ where $\vect{x}_n$ is the current approximation of the optimum and $g$ is the function that gathers all the equality and inequality constraints (violated values only)

getMaximumEvaluationNumber()¶

Accessor to maximum allowed number of evaluations.

Returns:

Nint: Maximum allowed number of evaluations.

getMaximumIterationNumber()¶

Accessor to maximum allowed number of iterations.

Returns:

Nint: Maximum allowed number of iterations.

getMaximumRelativeError()¶

Accessor to maximum allowed relative error.

Returns:

maximumRelativeErrorfloat: Maximum allowed relative error, where the relative error is defined by $\epsilon^r_n=\epsilon^a_n/\|\vect{x}_{n+1}\|_{\infty}$ if $\|\vect{x}_{n+1}\|_{\infty}\neq 0$ , else $\epsilon^r_n=-1$ .

getMaximumResidualError()¶

Accessor to maximum allowed residual error.

Returns:

maximumResidualErrorfloat: Maximum allowed residual error, where the residual error is defined by $\epsilon^r_n=\frac{\|f(\vect{x}_{n+1})-f(\vect{x}_{n})\|}{\|f(\vect{x}_{n+1})\|}$ if $\|f(\vect{x}_{n+1})\|\neq 0$ , else $\epsilon^r_n=-1$ .

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getProblem()¶

Accessor to optimization problem.

Returns:

problemOptimizationProblem: Optimization problem.

getResult()¶

Accessor to optimization result.

Returns:

resultOptimizationResult: Result class.

getSeed()¶

Random generator seed accessor.

Returns:

seedint: Seed.

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getStartingPoint()¶

Accessor to starting point.

Returns:

startingPointPoint: Starting point.

getStartingSample()¶

Accessor to the sample of starting points.

Returns:

startingSampleSample: The initial population.

getVerbose()¶

Accessor to the verbosity flag.

Returns:

verbosebool: Verbosity flag state.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

run()¶: Launch the optimization.

setAlgorithmName(algoName)¶

Accessor to the algorithm name.

Parameters:

algoNamestr: The identifier of the algorithm.

setBlockSize(blockSize)¶

Block size accessor.

Parameters:

blockSizeint: Batch evaluation granularity.

setGenerationNumber(generationNumber)¶

Generation number accessor.

Parameters:

genint: Number of generations to evolve. Ignored for the simulated_annealing algorithm.

setMaximumAbsoluteError(maximumAbsoluteError)¶

Accessor to maximum allowed absolute error.

Parameters:

maximumAbsoluteErrorfloat: Maximum allowed absolute error, where the absolute error is defined by $\epsilon^a_n=\|\vect{x}_{n+1}-\vect{x}_n\|_{\infty}$ where $\vect{x}_{n+1}$ and $\vect{x}_n$ are two consecutive approximations of the optimum.

setMaximumConstraintError(maximumConstraintError)¶

Accessor to maximum allowed constraint error.

Parameters:

maximumConstraintErrorfloat: Maximum allowed constraint error, where the constraint error is defined by $\gamma_n=\|g(\vect{x}_n)\|_{\infty}$ where $\vect{x}_n$ is the current approximation of the optimum and $g$ is the function that gathers all the equality and inequality constraints (violated values only)

setMaximumEvaluationNumber(maximumEvaluationNumber)¶

Accessor to maximum allowed number of evaluations.

Parameters:

Nint: Maximum allowed number of evaluations.

setMaximumIterationNumber(maximumIterationNumber)¶

Accessor to maximum allowed number of iterations.

Parameters:

Nint: Maximum allowed number of iterations.

setMaximumRelativeError(maximumRelativeError)¶

Accessor to maximum allowed relative error.

Parameters:

maximumRelativeErrorfloat: Maximum allowed relative error, where the relative error is defined by $\epsilon^r_n=\epsilon^a_n/\|\vect{x}_{n+1}\|_{\infty}$ if $\|\vect{x}_{n+1}\|_{\infty}\neq 0$ , else $\epsilon^r_n=-1$ .

setMaximumResidualError(maximumResidualError)¶

Accessor to maximum allowed residual error.

Parameters:

Maximum allowed residual error, where the residual error is defined by
:math:`epsilon^r_n=frac{|f(vect{x}_{n+1})-f(vect{x}_{n})|}{|f(vect{x}_{n+1})|}`
if :math:`|f(vect{x}_{n+1})|neq 0`, else :math:`epsilon^r_n=-1`.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setProblem(problem)¶

Accessor to optimization problem.

Parameters:

problemOptimizationProblem: Optimization problem.

setProgressCallback(*args)¶

Set up a progress callback.

Can be used to programmatically report the progress of an optimization.

Parameters:

callbackcallable: Takes a float as argument as percentage of progress.

Examples

>>> import sys
>>> import openturns as ot
>>> rosenbrock = ot.SymbolicFunction(['x1', 'x2'], ['(1-x1)^2+100*(x2-x1^2)^2'])
>>> problem = ot.OptimizationProblem(rosenbrock)
>>> solver = ot.OptimizationAlgorithm(problem)
>>> solver.setStartingPoint([0, 0])
>>> solver.setMaximumResidualError(1.e-3)
>>> solver.setMaximumEvaluationNumber(10000)
>>> def report_progress(progress):
...     sys.stderr.write('-- progress=' + str(progress) + '%\n')
>>> solver.setProgressCallback(report_progress)
>>> solver.run()

setResult(result)¶

Accessor to optimization result.

Parameters:

resultOptimizationResult: Result class.

setSeed(seed)¶

Random generator seed accessor.

Parameters:

seedint: Seed.

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters:

idint: Internal unique identifier.

setStartingPoint(point)¶

Accessor to starting point.

Parameters:

startingPointPoint: Starting point.

setStartingSample(startingSample)¶

Accessor to the sample of starting points.

Parameters:

startingSample2-d sequence of float: The initial population.

setStopCallback(*args)¶

Set up a stop callback.

Can be used to programmatically stop an optimization.

Parameters:

callbackcallable: Returns an int deciding whether to stop or continue.

Examples

>>> import openturns as ot
>>> rosenbrock = ot.SymbolicFunction(['x1', 'x2'], ['(1-x1)^2+100*(x2-x1^2)^2'])
>>> problem = ot.OptimizationProblem(rosenbrock)
>>> solver = ot.OptimizationAlgorithm(problem)
>>> solver.setStartingPoint([0, 0])
>>> solver.setMaximumResidualError(1.e-3)
>>> solver.setMaximumEvaluationNumber(10000)
>>> def ask_stop():
...     return True
>>> solver.setStopCallback(ask_stop)
>>> solver.run()

setVerbose(verbose)¶

Accessor to the verbosity flag.

Parameters:

verbosebool: Verbosity flag state.

setVisibility(visible)¶

Accessor to the object’s visibility state.

Parameters:

visiblebool: Visibility flag.

Examples using the class¶

Multi-objective optimization using Pagmo

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

Pagmo¶

Examples using the class¶