DrawParallelCoordinates

(Source code, png, hires.png, pdf)

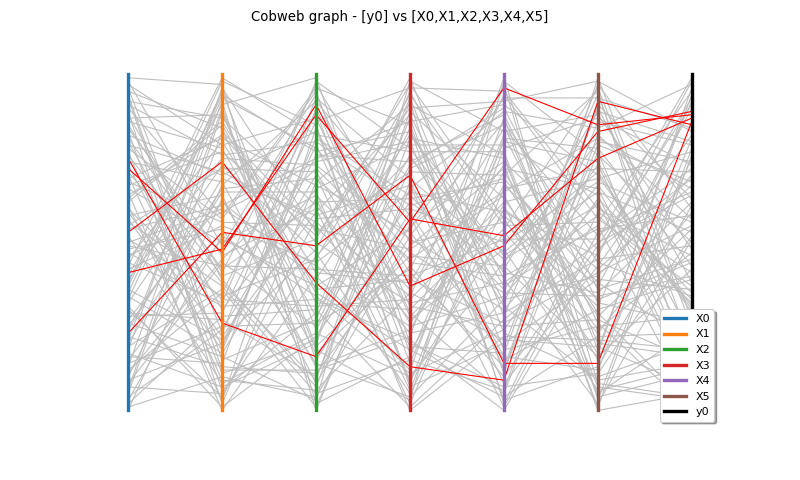
../../_images/DrawParallelCoordinates.png
DrawParallelCoordinates(inputSample, outputSample, minValue, maxValue, color, quantileScale=True)

Draw a parallel coordinates plot.

Parameters:
inputSample2-d sequence of float of dimension n

Input sample \vect{X}.

outputSample2-d sequence of float of dimension 1

Output sample Y.

Ymin, Ymaxfloat such that Ymax > Ymin

Values to select lines which will colore in color. Must be in [0,1] if quantileScale=True.

colorstr

Color of the specified curves.

quantileScalebool

Flag indicating the scale of the Ymin and Ymax. If quantileScale=True, they are expressed in the rank based scale; otherwise, they are expressed in the Y-values scale.

Returns:
graphGraph

The graph object

Notes

Let’s suppose a model f: \Rset^n \mapsto \Rset, where f(\vect{X})=Y. The parallel coordinates graph enables to visualize all the combinations of the input variables which lead to a specific range of the output variable.

Each column represents one component X_i of the input vector \vect{X}. The last column represents the scalar output variable Y.

For each point \vect{X}^j of inputSample, each component X_i^j is noted on its respective axe and the last mark is the one which corresponds to the associated Y^j. A line joins all the marks. Thus, each point of the sample corresponds to a particular line on the graph.

The scale of the axes are quantile based : each axe runs between 0 and 1 and each value is represented by its quantile with respect to its marginal empirical distribution.

It is interesting to select, among those lines, the ones which correspond to a specific range of the output variable. These particular lines selected are colored differently in color. This specific range is defined with Ymin and Ymax in the quantile based scale of Y or in its specific scale. In that second case, the range is automatically converted into a quantile based scale range.

Examples

>>> import openturns as ot
>>> from openturns.viewer import View

Generate a random sample from a Normal distribution:

>>> ot.RandomGenerator.SetSeed(0)
>>> inputSample = ot.Normal(2).getSample(15)
>>> inputSample.setDescription(['X0', 'X1'])
>>> formula = ['cos(X0)+cos(2*X1)']
>>> model = ot.SymbolicFunction(['X0', 'X1'], formula)
>>> outputSample = model(inputSample)

Draw a parallel plot:

>>> parplot = ot.VisualTest.DrawParallelCoordinates(inputSample, outputSample, 1.0, 2.0, 'red', False)
>>> View(parplot).show()