Note
Go to the end to download the full example code
Create a linear model¶
In this example we create a surrogate model using linear model approximation.
The following 2-dimensional function is used in this example
.
import openturns as ot
import openturns.viewer as viewer
Generation of the data set¶
We first generate the data and we add noise to the output observations:
ot.RandomGenerator.SetSeed(0)
distribution = ot.Normal(2)
distribution.setDescription(["x", "y"])
func = ot.SymbolicFunction(["x", "y"], ["2 * x - y + 3 + 0.05 * sin(0.8*x)"])
input_sample = distribution.getSample(30)
epsilon = ot.Normal(0, 0.1).getSample(30)
output_sample = func(input_sample) + epsilon
Linear regression¶
Let us run the linear model algorithm using the LinearModelAlgorithm class and get the associated results :
algo = ot.LinearModelAlgorithm(input_sample, output_sample)
result = algo.getResult()
Residuals analysis¶
We can now analyse the residuals of the regression on the training data. For clarity purposes, only the first 5 residual values are printed.
residuals = result.getSampleResiduals()
print(residuals[:5])
[ y0 ]
0 : [ 0.186748 ]
1 : [ -0.117266 ]
2 : [ -0.039708 ]
3 : [ 0.10813 ]
4 : [ -0.0673202 ]
Alternatively, the standardized or studentized residuals can be used:
stdresiduals = result.getStandardizedResiduals()
print(stdresiduals[:5])
[ v0 ]
0 : [ 1.80775 ]
1 : [ -1.10842 ]
2 : [ -0.402104 ]
3 : [ 1.03274 ]
4 : [ -0.633913 ]
Similarly, we can also obtain the underyling distribution characterizing the residuals:
print(result.getNoiseDistribution())
Normal(mu = 0, sigma = 0.110481)
ANOVA table¶
In order to post-process the linear regression results, the LinearModelAnalysis class can be used:
analysis = ot.LinearModelAnalysis(result)
print(analysis)
Basis( [[x,y]->[1],[x,y]->[x],[x,y]->[y]] )
Coefficients:
| Estimate | Std Error | t value | Pr(>|t|) |
--------------------------------------------------------------------
[x,y]->[1] | 2.99847 | 0.0204173 | 146.859 | 9.82341e-41 |
[x,y]->[x] | 2.02079 | 0.0210897 | 95.8186 | 9.76973e-36 |
[x,y]->[y] | -0.994327 | 0.0215911 | -46.0527 | 3.35854e-27 |
--------------------------------------------------------------------
Residual standard error: 0.11048 on 27 degrees of freedom
F-statistic: 5566.3 , p-value: 0
---------------------------------
Multiple R-squared | 0.997581 |
Adjusted R-squared | 0.997401 |
---------------------------------
---------------------------------
Normality test | p-value |
---------------------------------
Anderson-Darling | 0.456553 |
Cramer-Von Mises | 0.367709 |
Chi-Squared | 0.669183 |
Kolmogorov-Smirnov | 0.578427 |
---------------------------------
The results seem to indicate that the linear hypothesis can be accepted. Indeed, the R-Squared value is nearly 1. Furthermore, the adjusted value, which takes into account the data set size and the number of hyperparameters, is similar to R-Squared.
We can also notice that the Fisher-Snedecor and Student p-values detailed above are lower than 1%. This ensures an acceptable quality of the linear model.
Graphical analyses¶
Let us compare model and fitted values:
graph = analysis.drawModelVsFitted()
view = viewer.View(graph)
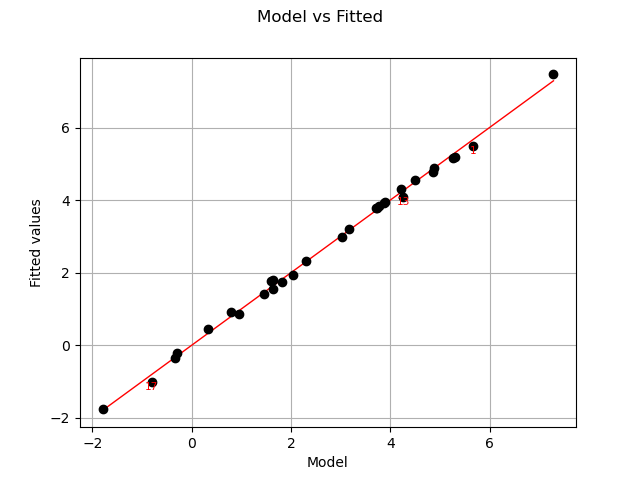
The previous figure seems to indicate that the linearity hypothesis is accurate.
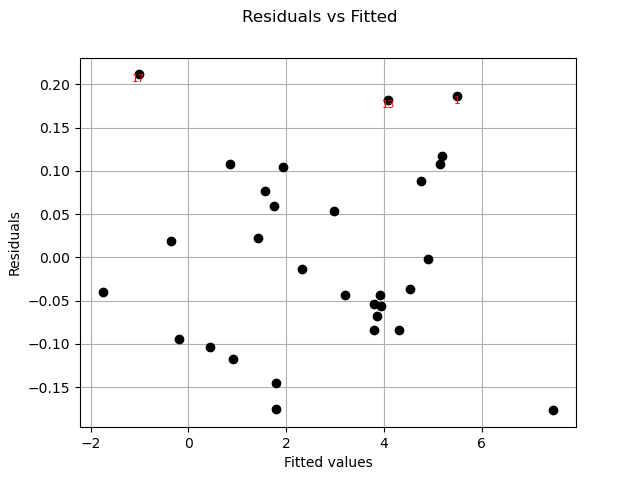
Residuals can be plotted against the fitted values.
graph = analysis.drawResidualsVsFitted()
view = viewer.View(graph)
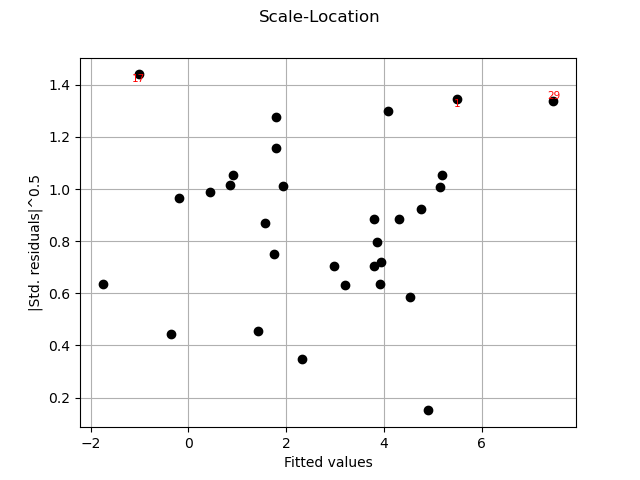
graph = analysis.drawScaleLocation()
view = viewer.View(graph)
graph = analysis.drawQQplot()
view = viewer.View(graph)
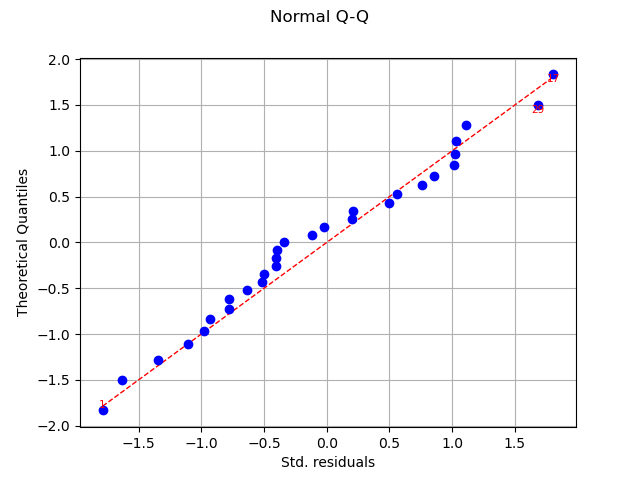
In this case, the two distributions are very close: there is no obvious outlier.
Cook’s distance measures the impact of every individual data point on the linear regression, and can be plotted as follows:
graph = analysis.drawCookDistance()
view = viewer.View(graph)
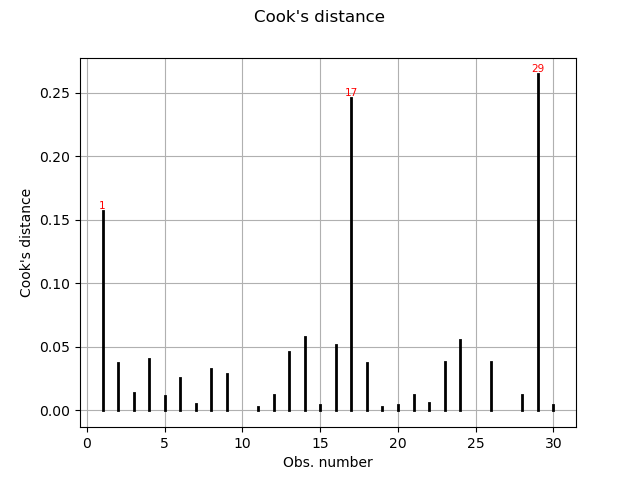
This graph shows us the index of the points with disproportionate influence.
One of the components of the computation of Cook’s distance at a given point is that point’s leverage. High-leverage points are far from their closest neighbors, so the fitted linear regression model must pass close to them.
graph = analysis.drawResidualsVsLeverages()
view = viewer.View(graph)
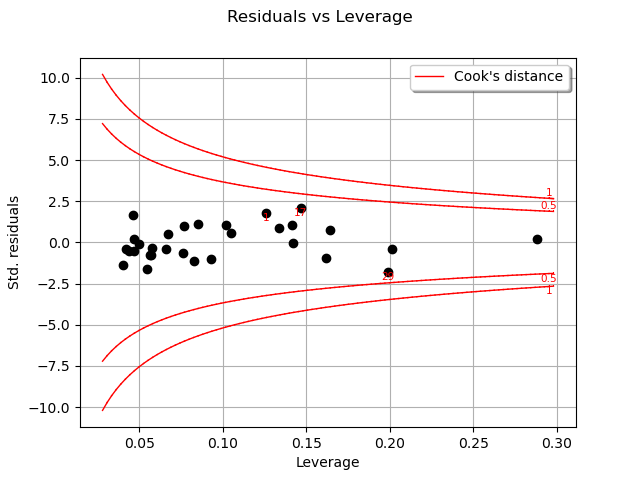
In this case, there seem to be no obvious influential outlier characterized by large leverage and residual values, as is also shown in the figure below:
Similarly, we can also plot Cook’s distances as a function of the sample leverages:
graph = analysis.drawCookVsLeverages()
view = viewer.View(graph)
![Cook's dist vs Leverage h[ii]/(1-h[ii])](../../_images/sphx_glr_plot_linear_model_007.png)
Finally, we give the intervals for each estimated coefficient (95% confidence interval):
alpha = 0.95
interval = analysis.getCoefficientsConfidenceInterval(alpha)
print("confidence intervals with level=%1.2f : " % (alpha))
print("%s" % (interval))
confidence intervals with level=0.95 :
[2.95657, 3.04036]
[1.97751, 2.06406]
[-1.03863, -0.950026]
 OpenTURNS
OpenTURNS