Note

Go to the end to download the full example code

Taylor approximations

In this example we build a local approximation of a model using the Taylor decomposition using the LinearTaylor class.

We consider the function h : \Rset^2 \rightarrow \Rset^2 defined by:

h(\vect{x}) = \left( \cos(x_1 + x_2), (x_2 + 1) e^{x_1 - 2 x_2} \right).

for any \vect{x} \in \Rset^2. The metamodel \widehat{h} is is an approximation of the model h:

\vect{y} \, \approx \, \widehat{h}(\vect{x})

for any \vect{x} \in \Rset^2. In this example, we consider two different approximations:

  • the first order Taylor expansion,

  • the second order Taylor expansion.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

Define the model

Prepare some data.

formulas = ["cos(x1 + x2)", "(x2 + 1) * exp(x1 - 2 * x2)"]
model = ot.SymbolicFunction(["x1", "x2"], formulas)

Center of the approximation.

x0 = [-0.4, -0.4]

Drawing bounds.

a = -0.4
b = 0.0

First order Taylor expansion

Let \vect{x}_0 \in \Rset^2 be a reference point where the linear approximation is evaluated. The first order Taylor expansion is:

\widehat{h}(\vect{x}) \, = \, h(\vect{x}_0) \, + \, \sum_{i=1}^{n_{X}} \; \frac{\partial h}{\partial x_i}(\vect{x}_0).\left(x_i - x_{0,i} \right)

for any \vect{x} \in \Rset^2.

Create a linear (first-order) Taylor approximation.

algo = ot.LinearTaylor(x0, model)
algo.run()
responseSurface = algo.getMetaModel()

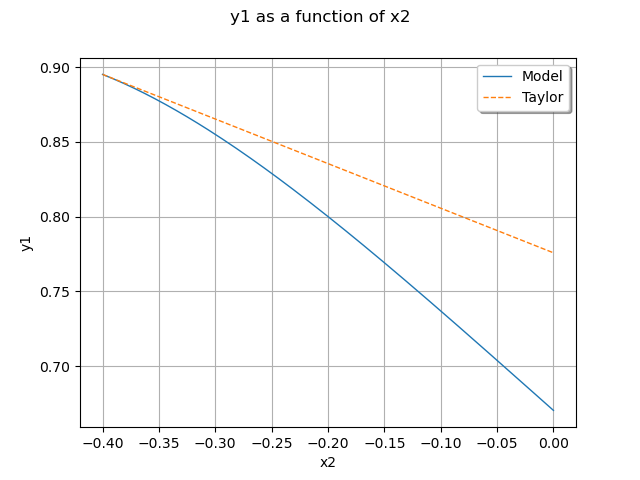
Plot the second output of our model with x_1=x_{0,1}.

graph = ot.ParametricFunction(model, [0], [x0[1]]).getMarginal(1).draw(a, b)
graph.setLegends(["Model"])
curve = (
    ot.ParametricFunction(responseSurface, [0], [x0[1]]).getMarginal(1).draw(a, b).getDrawable(0)
)
curve.setLegend("Taylor")
curve.setLineStyle("dashed")
graph.add(curve)
graph.setLegendPosition("topright")
graph.setColors(ot.Drawable.BuildDefaultPalette(2))
view = viewer.View(graph)
y1 as a function of x2

Second order Taylor expansion

Let \vect{x}_0 \in \Rset^2 be a reference point where the quadratic approximation is evaluated. The second order Taylor expansion is:

\widehat{h}(\vect{x}) \, = \, h(\vect{x}_0) \, + \, \sum_{i=1}^{n_{X}} \; \frac{\partial h}{\partial x_i}(\vect{x}_0).\left(x_i - x_{0,i} \right) \, + \, \frac{1}{2} \; \sum_{i,j=1}^{n_X} \; \frac{\partial^2 h}{\partial x_i \partial x_j}(\vect{x}_0).\left(x_i - x_{0,i} \right).\left(x_j - x_{0,j} \right)

for any \vect{x} \in \Rset^2.

Create a quadratic (second-order) Taylor approximation.

algo = ot.QuadraticTaylor(x0, model)
algo.run()
responseSurface = algo.getMetaModel()

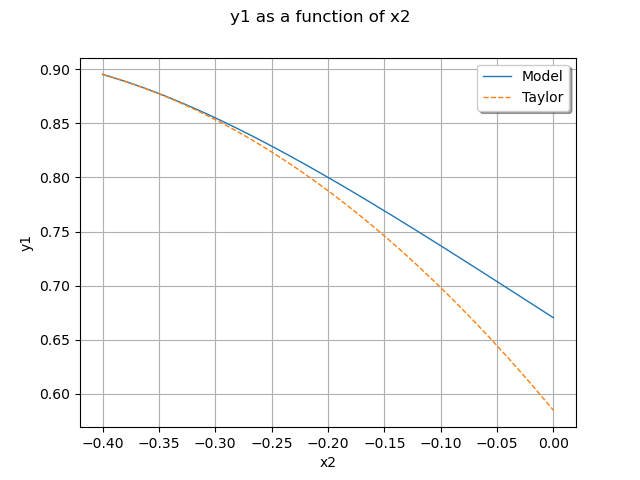
Plot second output of our model with x_1=x_{0,1}.

graph = ot.ParametricFunction(model, [0], [x0[1]]).getMarginal(1).draw(a, b)
graph.setLegends(["Model"])
curve = (
    ot.ParametricFunction(responseSurface, [0], [x0[1]]).getMarginal(1).draw(a, b).getDrawable(0)
)
curve.setLegend("Taylor")
curve.setLineStyle("dashed")
graph.add(curve)
graph.setLegendPosition("topright")
graph.setColors(ot.Drawable.BuildDefaultPalette(2))
view = viewer.View(graph)
plt.show()
y1 as a function of x2