Note
Go to the end to download the full example code
Evaluate the mean of a random vector by simulations¶
Abstract¶
We introduce the ExpectationSimulationAlgorithm class which implements an incremental Monte Carlo sampling algorithm to estimate the mean of a random vector.
import openturns as ot
import openturns.viewer as otv
from matplotlib import pylab as plt
We shall use this algorithm for the Ishigami function that we load from the usecases module :
from openturns.usecases import ishigami_function
im = ishigami_function.IshigamiModel()
The Ishigami model and the distribution of the input variables are stored in the im object :
model = im.model
distribution = im.distributionX
We create a random vector that follows the distribution of the input variables.
inputVector = ot.RandomVector(distribution)
The output vector is a CompositeRandomVector.
outputVector = ot.CompositeRandomVector(model, inputVector)
The mean of the output vector is
print("Mean of the output random vector : %.5f" % im.expectation)
Mean of the output random vector : 3.50000
We define the algorithm simply by calling it with the output vector :
algo = ot.ExpectationSimulationAlgorithm(outputVector)
We can also set the algorithm parameters :
algo.setMaximumOuterSampling(80000)
algo.setBlockSize(1)
algo.setCoefficientOfVariationCriterionType("NONE")
We are then ready to launch the algorithm and store the result.
algo.run()
result = algo.getResult()
As usual for Monte Carlo estimation we can draw the convergence history.
graphConvergence = algo.drawExpectationConvergence()
view = otv.View(graphConvergence)
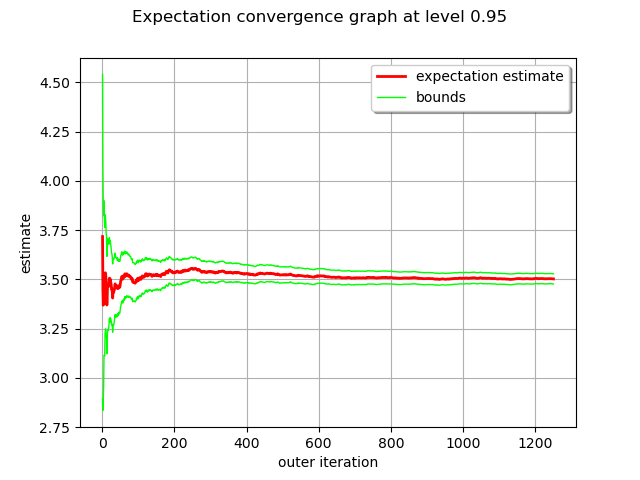
The result obtained with the previous algorithm is an instance of the :class:~openturns.ExpectationSimulationResult` class.
The expected value of the mean is given by the getExpectationEstimate method :
expectation = result.getExpectationEstimate()
print("Estimated mean of the output random vector : %.5f" % expectation[0])
Estimated mean of the output random vector : 3.50261
The variance and standard deviation of the estimated mean are respectively given by getVarianceEstimate and getStandardDeviation:
expectationVariance = result.getVarianceEstimate()
print(
"Variance of the estimated mean of the output random vector : %.5f"
% expectationVariance[0]
)
standardDeviation = result.getStandardDeviation()
print("Standard deviation : %.5f" % standardDeviation[0])
Variance of the estimated mean of the output random vector : 0.00017
Standard deviation : 0.01316
This variance and this standard deviation must not to be confused with the variance and the standard deviation of the Ishigami model!
print("Ishigami variance : %.5f" % im.variance)
print("Ishigami standard deviation : %.5f" % im.variance ** (1 / 2))
Ishigami variance : 13.84459
Ishigami standard deviation : 3.72083
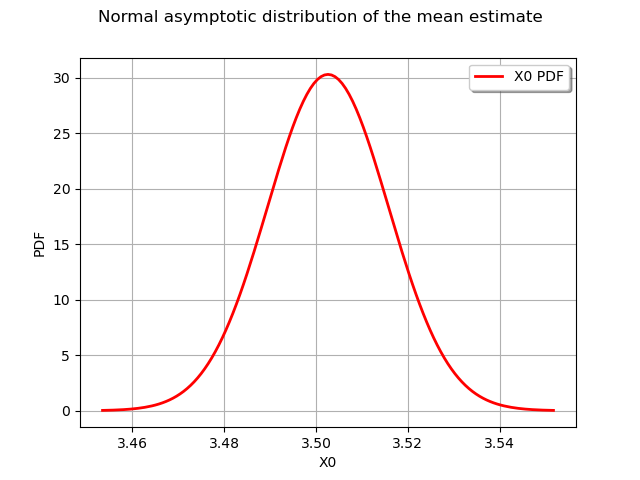
The asymptotic confidence distribution of the output random vector mean estimate is
expectationDistribution = result.getExpectationDistribution()
print(expectationDistribution)
Normal(mu = 3.50261, sigma = 0.0131575)
Let us draw it:
graphExpectationDistribution = expectationDistribution.drawPDF()
graphExpectationDistribution.setTitle(
"Normal asymptotic distribution of the mean estimate"
)
view = otv.View(graphExpectationDistribution)
Display all figures
plt.show()
 OpenTURNS
OpenTURNS