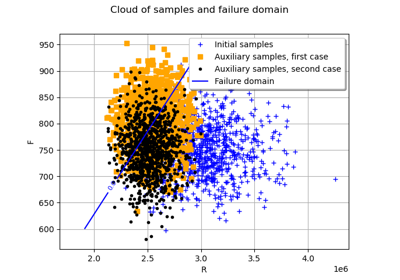
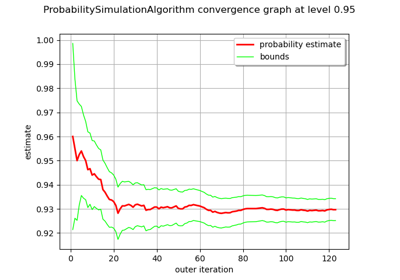
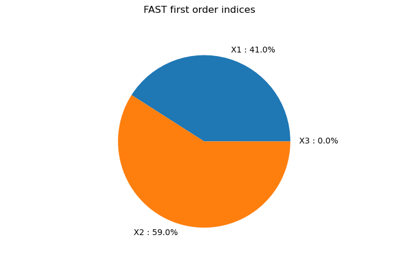
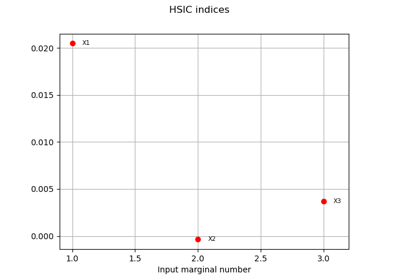
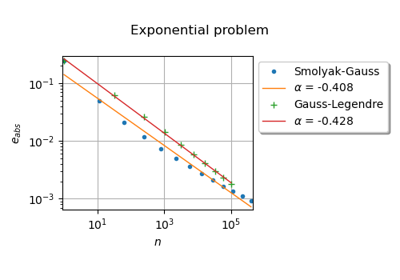
Reliability & Sensitivity¶
Central dispersion¶
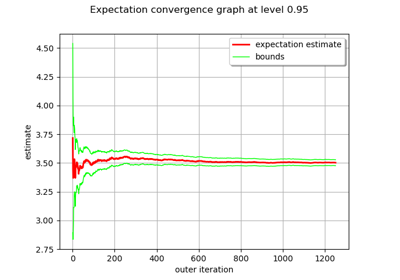
Evaluate the mean of a random vector by simulations
Reliability¶

Estimate a probability with Latin Hypercube Sampling

Use the Adaptive Directional Stratification Algorithm

Use the post-analytical importance sampling algorithm
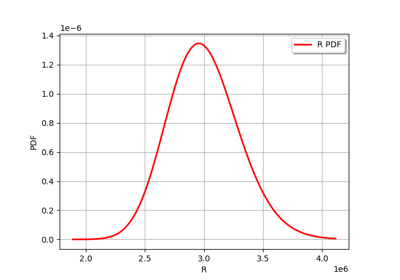
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
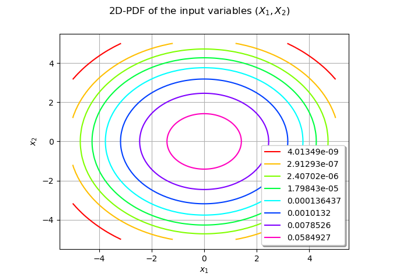
Use the FORM algorithm in case of several design points
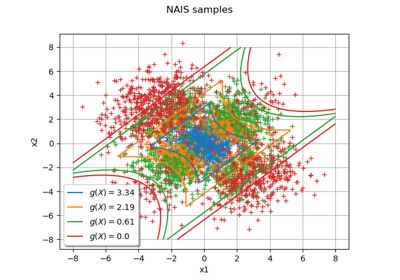
Non parametric Adaptive Importance Sampling (NAIS)

Test the design point with the Strong Maximum Test
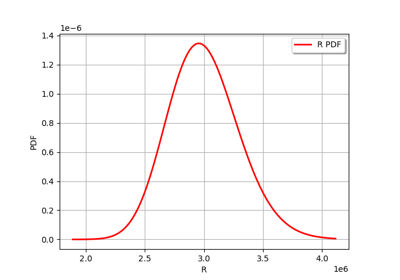
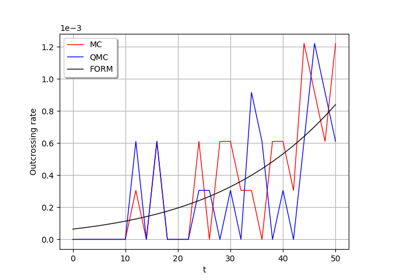
Axial stressed beam : comparing different methods to estimate a probability
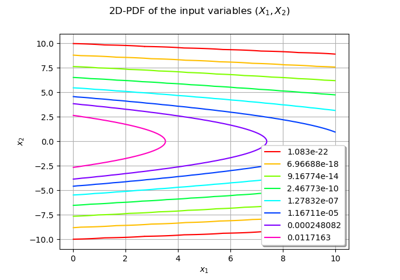
An illustrated example of a FORM probability estimate
Reliability processes¶
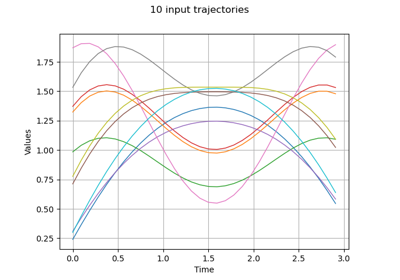
Estimate Sobol indices on a field to point function
Sensitivity analysis¶
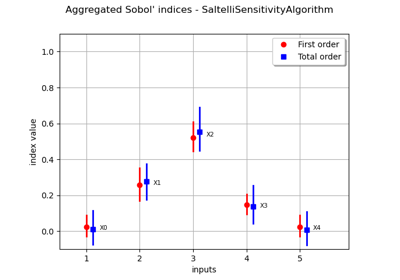
Estimate Sobol’ indices for a function with multivariate output
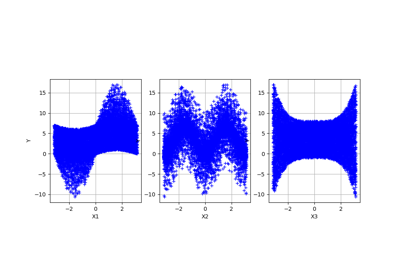
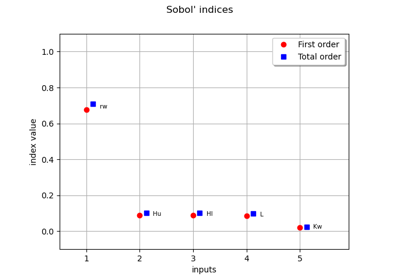
Example of sensitivity analyses on the wing weight model
Design of experiments¶
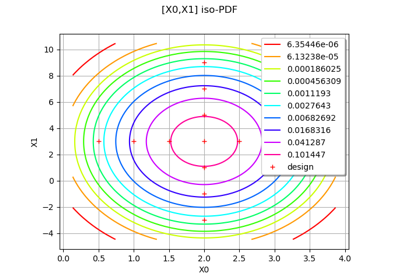
Create mixed deterministic and probabilistic designs of experiments
Create a design of experiments with discrete and continuous variables
 OpenTURNS
OpenTURNS