A simple stressed beam¶
We consider a simple beam stressed by a traction load F at both sides.

Beam geometry¶
The geometry is supposed to be deterministic; the diameter D is equal to:
By definition, the yield stress is the load divided by the surface. Since the surface is , the stress is:
Failure occurs when the beam plastifies, i.e. when the axial stress gets larger than the yield stress:
where is the strength.
Therefore, the limit state function is:
for any .
The value of the parameter is such that:
which leads to the equation:
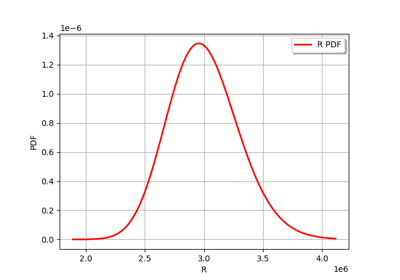
We consider the following distribution functions.
Variable |
Distribution |
|---|---|
R |
LogNormal( |
F |
Normal( |
where
and
are the mean and the variance of
.
The failure probability is:
The exact is
API documentation¶
- class AxialStressedBeam
Data class for the axial stressed beam example.
Examples
>>> from openturns.usecases import stressed_beam >>> # Load the axial stressed beam >>> sm = stressed_beam.AxialStressedBeam()
- Attributes:
- dimThe dimension of the problem
dim=2.
- DConstant
Diameter D = 0.02 (m)
- modelSymbolicFunction
The limit state function.
- muRConstant
muR=3.0e6, yield strength mean
- sigmaRConstant
sigmaR = 3.0e5, yield strength variance
- distribution_RLogNormalMuSigma distribution of the yield strength
ot.LogNormalMuSigma(muR, sigmaR, 0.0).getDistribution()
- muFConstant
muF=750.0, traction load mean
- sigmaFConstant
sigmaR = 50.0, traction load variance
- distribution_FNormal distribution of the traction load
ot.Normal(muF, sigmaF)
- distributionComposedDistribution
The joint distribution of the inpput parameters.
Examples based on this use case¶

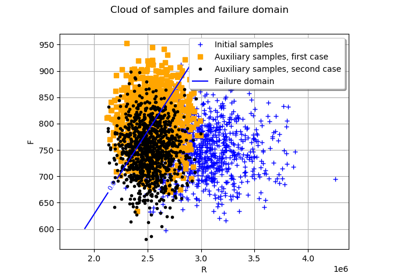
Estimate a probability with Latin Hypercube Sampling
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
Axial stressed beam : comparing different methods to estimate a probability
 OpenTURNS
OpenTURNS