The cantilever beam model¶
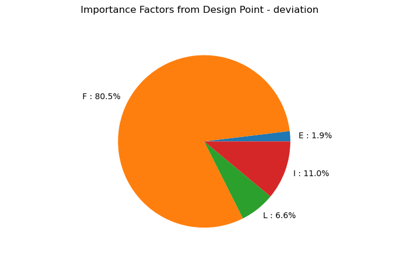
We are interested in the vertical deviation of a diving board created by a child diver. We consider a child whose weight generates a force approximately equal to 300N (i.e. almost 30 kg). Because of the uncertainties in the weight of the person, we consider that the force is a random variable. The length of the diving board is between 2.5 m and 2.6 m. The Young modulus is uncertain and between 65 and 75 GPa, which corresponds to the fiberglass material, a material often used for diving boards. Uncertainties in the production of the material are taken into account in the Young modulus and the section modulus of the board.
We consider a cantilever beam defined by its Young’s modulus , its length
and its
section modulus
.
One end of the cantilever beam is built in a wall and we apply a concentrated bending load
at
the other end of the beam, resulting in a deviation
.

The beam geometry¶
Inputs¶
: Young modulus (Pa), Beta(
,
, a =
,
)
: Loading (N), Lognormal(
,
, shift=0.0)
: Length of beam (m), Uniform(min=2.5, max= 2.6)
: Moment of inertia (
), Beta(
,
,
,
).
In the previous table and
are the mean and the standard deviation of
.
We assume that the random variables ,
,
and
are dependent
and associated with a gaussian copula which correlation matrix is:
In other words, we consider that the variables and
are negatively correlated:
when the length
increases, the moment of inertia
decreases.
Output¶
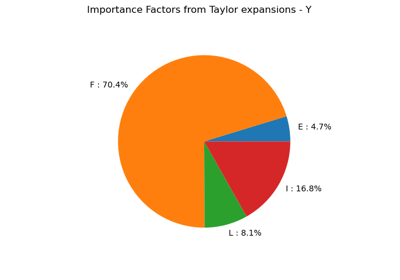
The vertical displacement at free end of the cantilever beam is:
A typical event of interest is when the beam deviation is too large which is a failure:
API documentation¶
- class CantileverBeam
Data class for the cantilever beam example.
Examples
>>> from openturns.usecases import cantilever_beam >>> # Load the cantilever beam model >>> cb = cantilever_beam.CantileverBeam()
- Attributes:
- dimThe dimension of the problem
dim=4.
- EBeta distribution
ot.Beta(0.9, 3.5, 65.0e9, 75.0e9)
- FLogNormal distribution
ot.LogNormalMuSigma()([300.0, 30.0, 0.0])
- LUniform distribution
ot.Uniform(2.5, 2.6)
- IBeta distribution
ot.Beta(2.5, 4.0, 1.3e-7, 1.7e-7)
- modelSymbolicFunction, the physical model of the cantilever beam.
- RCorrelationMatrix
Correlation matrix used to define the copula.
- copulaNormalCopula
Copula of the model.
- distributionComposedDistribution
The joint distribution of the parameters.
- independentDistributionComposedDistribution
The joint distribution of the parameters with independent copula.
Examples based on this use case¶
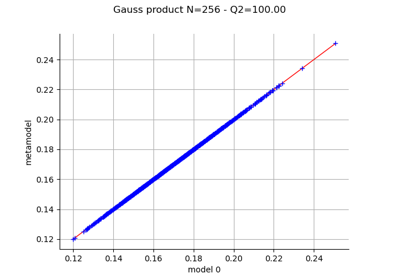
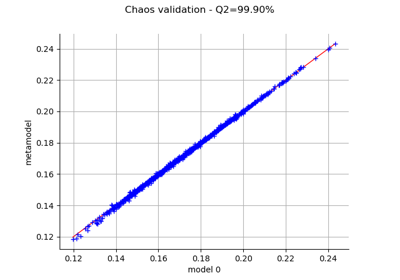
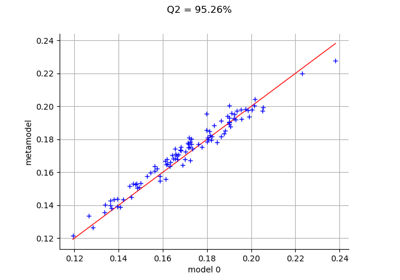
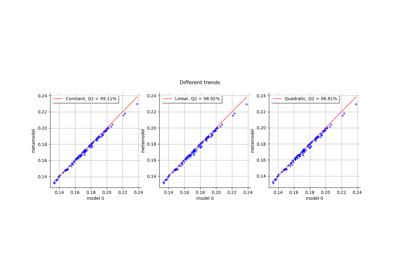
Create a polynomial chaos metamodel by integration on the cantilever beam

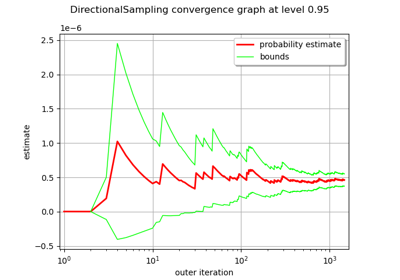
Use the Adaptive Directional Stratification Algorithm
 OpenTURNS
OpenTURNS