Note

Go to the end to download the full example code.

Kriging : multiple input dimensions

In this example we are going to create an approximation of a model response using a kriging model. We consider a bidimensional function with Gaussian inputs. Then we create a kriging metamodel with a constant basis and a SquaredExponential covariance.

We consider the function

g(\vect{x}) = \cos(x_1 + x_2)

for any \vect{x} \in \Rset^2. We assume that X_1 and X_2 have a Gaussian distribution :

X_1 \sim \mathcal{N}(0,1) \textrm{ and } X_2 \sim \mathcal{N}(0,1).

import openturns as ot
import openturns.viewer as viewer

ot.Log.Show(ot.Log.NONE)

We define the model.

dimension = 2
input_names = ["x1", "x2"]
formulas = ["cos(x1 + x2)"]
model = ot.SymbolicFunction(input_names, formulas)

We generate a simple Monte-Carlo input sample and evaluate the corresponding output sample.

distribution = ot.Normal(dimension)
samplesize = 15
x = distribution.getSample(samplesize)
y = model(x)

Then we create a Kriging metamodel, using a constant trend and a squared exponential covariance model.

basis = ot.ConstantBasisFactory(dimension).build()
covarianceModel = ot.SquaredExponential([0.1] * dimension, [1.0])
algo = ot.KrigingAlgorithm(x, y, covarianceModel, basis)
algo.run()
result = algo.getResult()
metamodel = result.getMetaModel()

It is not so easy to visualize a bidimensional function. In order to simplify the graphics, we consider the value of the function at the input x_{1,ref}=0.5. This amounts to create a ParametricFunction where the first variable x_1 (at input index 0) is set to 0.5.

x1ref = 0.5
metamodelAtXref = ot.ParametricFunction(metamodel, [0], [x1ref])
modelAtXref = ot.ParametricFunction(model, [0], [x1ref])

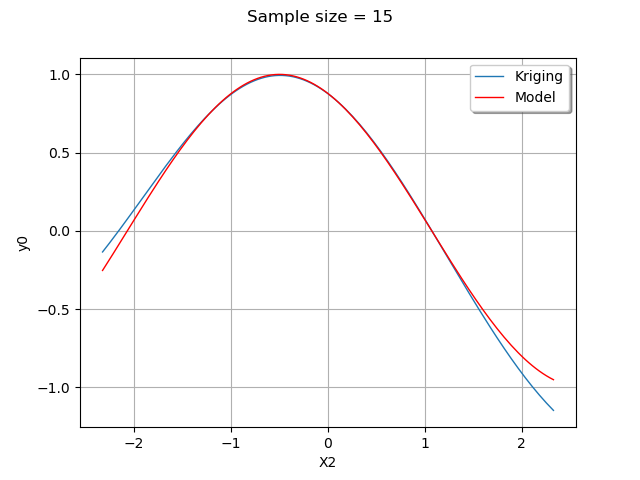
For this given value of x_1, we plot the model and the metamodel with x_2 from its 1% up to its 99% quantile. We configure the X title to “X2” because the default setting would state that this axis is the first value of the parametric function, which default name is “X0”.

x2min = ot.Normal().computeQuantile(0.01)[0]
x2max = ot.Normal().computeQuantile(0.99)[0]
graph = metamodelAtXref.draw(x2min, x2max)
graph.setLegends(["Kriging"])
curve = modelAtXref.draw(x2min, x2max)
curve.setLegends(["Model"])
curve.setColors(["red"])
graph.add(curve)
graph.setLegendPosition("upper right")
graph.setTitle("Sample size = %d" % (samplesize))
graph.setXTitle("X2")
view = viewer.View(graph)
Sample size = 15
view.ShowAll()

As we can see, the metamodel is quite accurate in this case. The metamodel is very close to the model in the center of the domain, where the density of the input distribution is highest.