MetaModelValidation¶
(Source code, png)

- class MetaModelValidation(*args)¶
Scores a metamodel in order to perform its validation.
- Parameters:
- outputSample2-d sequence of float
The output validation sample, not used during the learning step.
- metamodelPredictions: 2-d sequence of float
The output prediction sample from the metamodel.
Methods
Accessor to the mean squared error.
Compute the R2 score.
Plot a model vs metamodel graph for visual validation.
Accessor to the object's name.
Accessor to the output predictions from the metamodel.
getName()Accessor to the object's name.
Accessor to the output sample.
getResidualDistribution([smooth])Compute the non parametric distribution of the residual sample.
Compute the residual sample.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
Notes
A MetaModelValidation object is used for the validation of a metamodel. For that purpose, a dataset independent of the learning step, is used to score the surrogate model. Its main functionalities are :
compute the coefficient of determination
;
get the residual sample and its non parametric distribution ;
draw a validation graph presenting the metamodel predictions against the model observations.
More details on this topic are presented in Validation and cross validation of metamodels.
Examples
In this example, we introduce the sinus model and approximate it with a least squares metamodel. Then we validate this metamodel using a test sample.
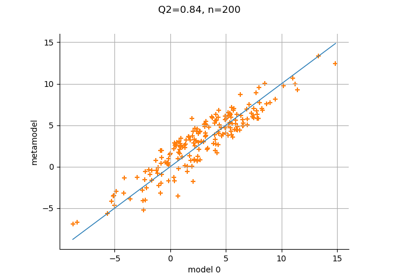
>>> import openturns as ot >>> from math import pi >>> dist = ot.Uniform(-pi / 2, pi / 2) >>> # Define the model >>> model = ot.SymbolicFunction(['x'], ['sin(x)']) >>> # We can build several types of models (kriging, polynomial chaos expansion, ...) >>> # We use here a least squares expansion on canonical basis and compare >>> # the metamodel with the model >>> # Build the metamodel using a train sample >>> x_train = dist.getSample(25) >>> y_train = model(x_train) >>> total_degree = 3 >>> polynomialCollection = [f'x^{degree + 1}' for degree in range(total_degree)] >>> basis = ot.SymbolicFunction(['x'], polynomialCollection) >>> designMatrix = basis(x_train) >>> myLeastSquares = ot.LinearLeastSquares(designMatrix, y_train) >>> myLeastSquares.run() >>> leastSquaresModel = myLeastSquares.getMetaModel() >>> metaModel = ot.ComposedFunction(leastSquaresModel, basis) >>> # Validate the metamodel using a test sample >>> x_test = dist.getSample(100) >>> y_test = model(x_test) >>> metamodelPredictions = metaModel(x_test) >>> val = ot.MetaModelValidation(y_test, metamodelPredictions) >>> # Compute the R2 score >>> r2Score = val.computeR2Score() >>> # Get the residual >>> residual = val.getResidualSample() >>> # Get the histogram of residuals >>> histoResidual = val.getResidualDistribution(False) >>> # Draw the validation graph >>> graph = val.drawValidation()
- __init__(*args)¶
- computeMeanSquaredError()¶
Accessor to the mean squared error.
- Returns:
- meanSquaredError
Point The mean squared error of each marginal output dimension.
- meanSquaredError
Notes
The sample mean squared error is:
where
is the sample size,
is the metamodel,
is the input experimental design and
is the output of the model.
If the output is multi-dimensional, the same calculations are repeated separately for each output marginal
for
where
is the output dimension.
- computeR2Score()¶
Compute the R2 score.
- Returns:
- r2Score
Point The coefficient of determination R2
- r2Score
Notes
The coefficient of determination
is the fraction of the variance of the output explained by the metamodel. It is defined as:
where
is the fraction of unexplained variance:
where
is the output of the physical model
,
is the variance of the output and
is the mean squared error of the metamodel:
The sample
is:
where
is the sample size,
is the metamodel,
is the input experimental design,
is the output of the model and
is the sample variance of the output:
where
is the output sample mean:
- drawValidation()¶
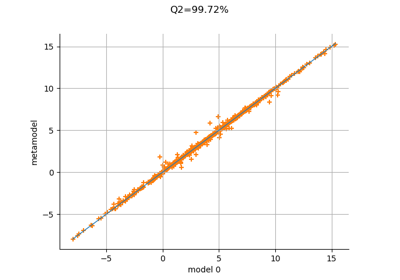
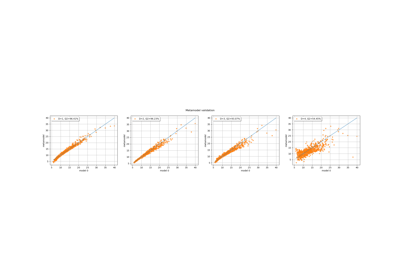
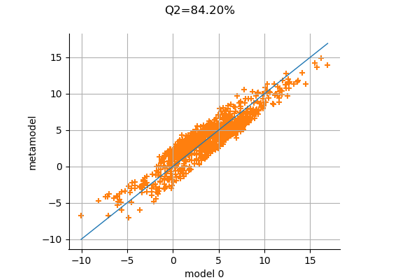
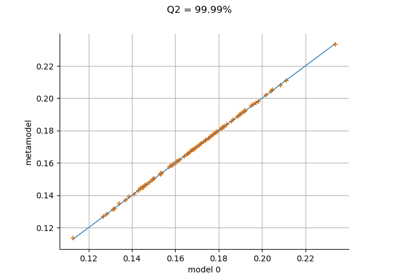
Plot a model vs metamodel graph for visual validation.
- Returns:
- graph
GridLayout The visual validation graph.
- graph
Notes
The plot presents the metamodel predictions depending on the model observations. If the points are close to the diagonal line of the plot, then the metamodel validation is satisfactory. Points which are far away from the diagonal represent outputs for which the metamodel is not accurate.
If the output is multi-dimensional, the graph has 1 row and
columns, where
is the output dimension.
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getMetamodelPredictions()¶
Accessor to the output predictions from the metamodel.
- Returns:
- outputMetamodelSample
Sample Output sample of the metamodel.
- outputMetamodelSample
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getOutputSample()¶
Accessor to the output sample.
- Returns:
- outputSample
Sample Output sample of a model evaluated apart.
- outputSample
- getResidualDistribution(smooth=True)¶
Compute the non parametric distribution of the residual sample.
- Parameters:
- smoothbool
Tells if distribution is smooth (true) or not. Default argument is true.
- Returns:
- residualDistribution
Distribution The residual distribution.
- residualDistribution
Notes
The residual distribution is built thanks to
KernelSmoothingif smooth argument is true. Otherwise, an histogram distribution is returned, thanks toHistogramFactory.
- getResidualSample()¶
Compute the residual sample.
- Returns:
- residual
Sample The residual sample.
- residual
Notes
The residual sample is given by :
for
where
is the sample size,
is the model observation,
is the metamodel and
is the
-th input observation.
If the output is multi-dimensional, the residual sample has dimension
, where
is the output dimension.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
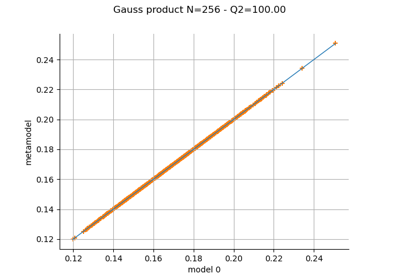
Create a polynomial chaos metamodel by integration on the cantilever beam
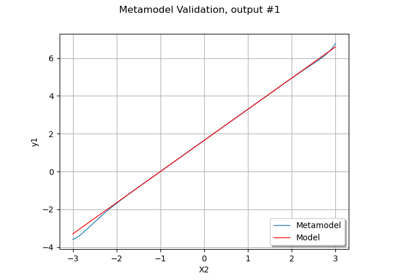
Create a polynomial chaos metamodel from a data set
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
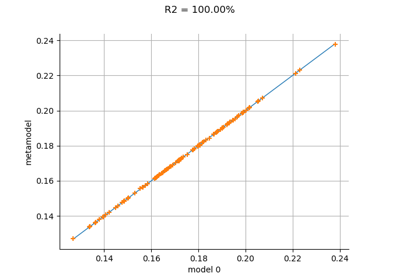
Gaussian Process Regression : cantilever beam model
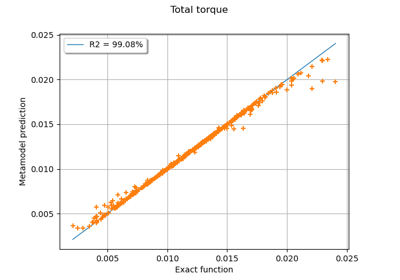
Example of multi output Kriging on the fire satellite model
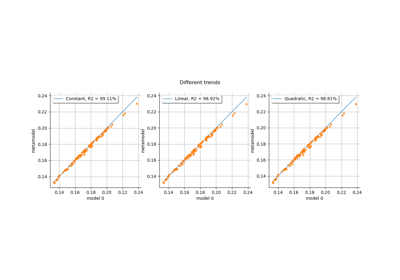
Kriging: choose a polynomial trend on the beam model
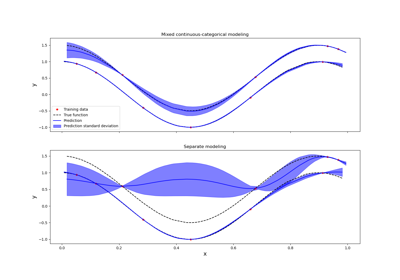
Kriging: metamodel with continuous and categorical variables
Estimate Sobol indices on a field to point function
Compute confidence intervals of a regression model from data
 OpenTURNS
OpenTURNS