Draw cross-cuts of multidimensional functions

This example shows how to represent multidimensional functions. When 2D plots are to draw, contours are used. We use 2D cross-sections to represent multidimensional objects when required, which leads to cross-cuts representations.

import otbenchmark as otb
import openturns.viewer as otv

problem = otb.ReliabilityProblem33()

event = problem.getEvent()
g = event.getFunction()

Compute the bounds of the domain

inputVector = event.getAntecedent()
distribution = inputVector.getDistribution()

inputDimension = distribution.getDimension()
inputDimension

3

alpha = 1 - 1.0e-5
bounds, marginalProb = distribution.computeMinimumVolumeIntervalWithMarginalProbability(
    alpha
)

referencePoint = distribution.getMean()
referencePoint

class=Point name=Unnamed dimension=3 values=[0,0,0]

crossCut = otb.CrossCutFunction(g, referencePoint)
_ = crossCut.draw(bounds)

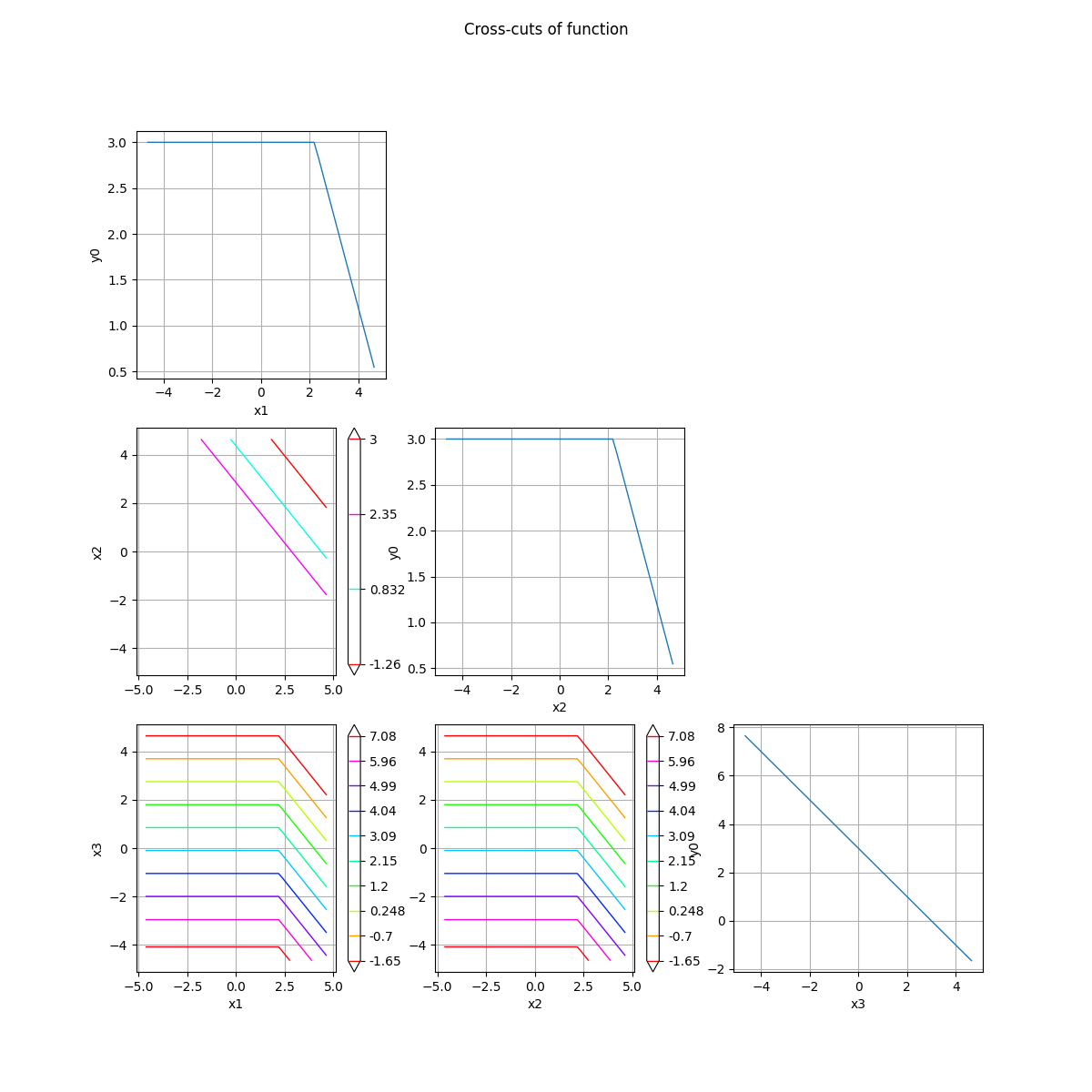
Let us explain this figure in detail, by describing each sub-plot from top to bottom, and from left to right:

• Fig. A,

• Fig. B, C,

• Fig. D, E, F.

Let be the reference point.

• Fig. A : represents , which is a function depending on only.

• Fig. B : represents the contours of the bi-dimensional function which depends on and .

• Fig. C : represents , which is a function depending on only.

• Fig. D : represents the contours of the bi-dimensional function which depends on and .

• Fig. E : represents the contours of the bi-dimensional function which depends on and .

• Fig. F : represents , which is a function depending on only.

otv.View.ShowAll()