RP33 analysis and 2D graphics

The objective of this example is to present problem 33 of the BBRC.

import otbenchmark as otb

problem = otb.ReliabilityProblem33()
print(problem)

name = RP33
event = class=ThresholdEventImplementation antecedent=class=CompositeRandomVector function=class=Function name=Unnamed implementation=class=FunctionImplementation name=Unnamed description=[x1,x2,x3,y0] evaluationImplementation=class=SymbolicEvaluation name=Unnamed inputVariablesNames=[x1,x2,x3] outputVariablesNames=[y0] formulas=[min(-x1 - x2 - x3 + 3 * sqrt(3), -x3 + 3)] gradientImplementation=class=SymbolicGradient name=Unnamed evaluation=class=SymbolicEvaluation name=Unnamed inputVariablesNames=[x1,x2,x3] outputVariablesNames=[y0] formulas=[min(-x1 - x2 - x3 + 3 * sqrt(3), -x3 + 3)] hessianImplementation=class=SymbolicHessian name=Unnamed evaluation=class=SymbolicEvaluation name=Unnamed inputVariablesNames=[x1,x2,x3] outputVariablesNames=[y0] formulas=[min(-x1 - x2 - x3 + 3 * sqrt(3), -x3 + 3)] antecedent=class=UsualRandomVector distribution=class=JointDistribution name=JointDistribution dimension=3 copula=class=IndependentCopula name=IndependentCopula dimension=3 marginal[0]=class=Normal name=Normal dimension=1 mean=class=Point name=Unnamed dimension=1 values=[0] sigma=class=Point name=Unnamed dimension=1 values=[1] correlationMatrix=class=CorrelationMatrix dimension=1 implementation=class=MatrixImplementation name=Unnamed rows=1 columns=1 values=[1] marginal[1]=class=Normal name=Normal dimension=1 mean=class=Point name=Unnamed dimension=1 values=[0] sigma=class=Point name=Unnamed dimension=1 values=[1] correlationMatrix=class=CorrelationMatrix dimension=1 implementation=class=MatrixImplementation name=Unnamed rows=1 columns=1 values=[1] marginal[2]=class=Normal name=Normal dimension=1 mean=class=Point name=Unnamed dimension=1 values=[0] sigma=class=Point name=Unnamed dimension=1 values=[1] correlationMatrix=class=CorrelationMatrix dimension=1 implementation=class=MatrixImplementation name=Unnamed rows=1 columns=1 values=[1] operator=class=Less name=Unnamed threshold=0
probability = 0.00257

event = problem.getEvent()
g = event.getFunction()

problem.getProbability()

0.00257

inputVector = event.getAntecedent()
distribution = inputVector.getDistribution()

inputDimension = distribution.getDimension()
inputDimension

3

alpha = 1 - 0.00001
bounds, marginalProb = distribution.computeMinimumVolumeIntervalWithMarginalProbability(
    alpha
)

referencePoint = distribution.getMean()
referencePoint

class=Point name=Unnamed dimension=3 values=[0,0,0]

crossCut = otb.CrossCutFunction(g, referencePoint)
_ = crossCut.draw(bounds)

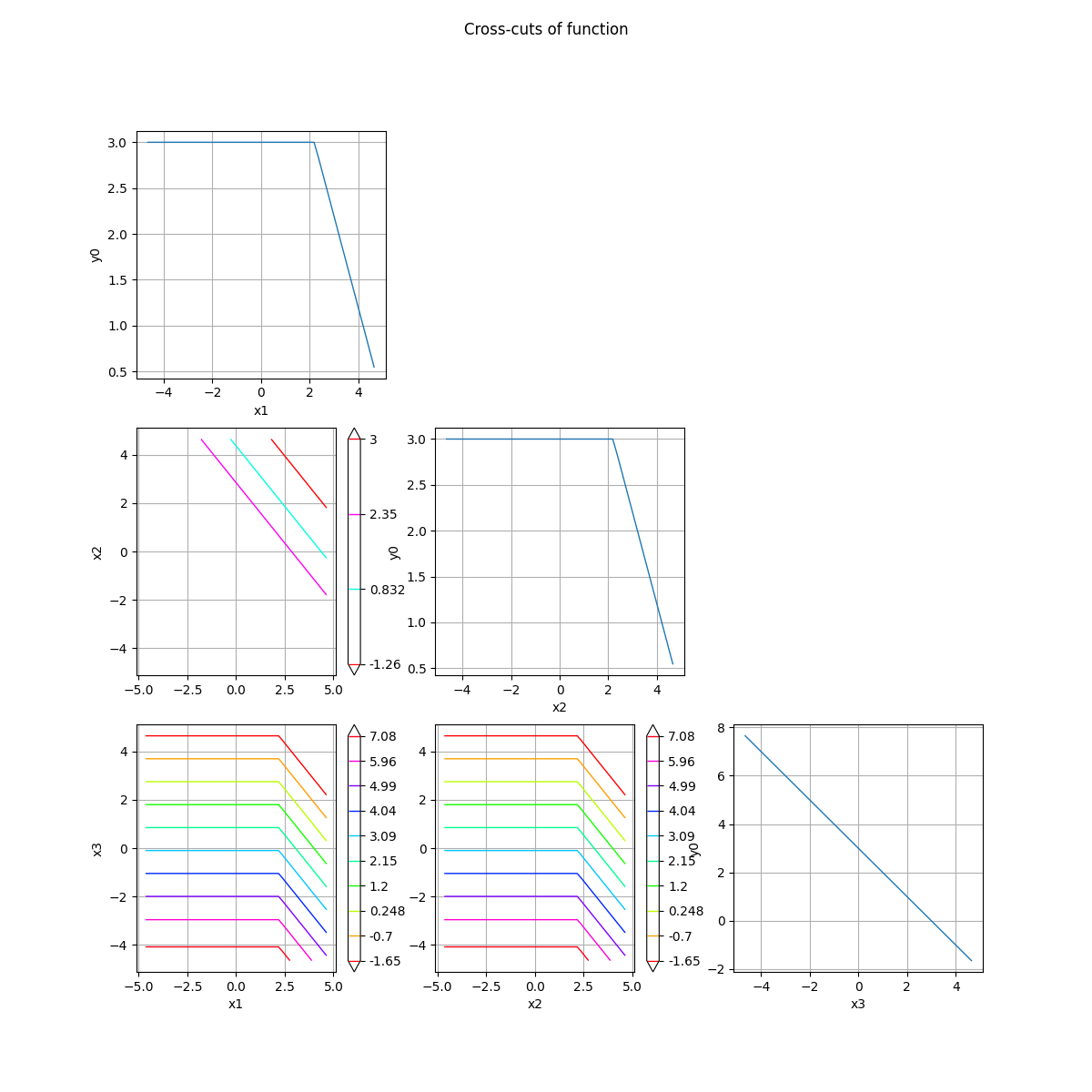
Plot cross-cuts of the distribution

crossCut = otb.CrossCutDistribution(distribution)

_ = crossCut.drawMarginalPDF()

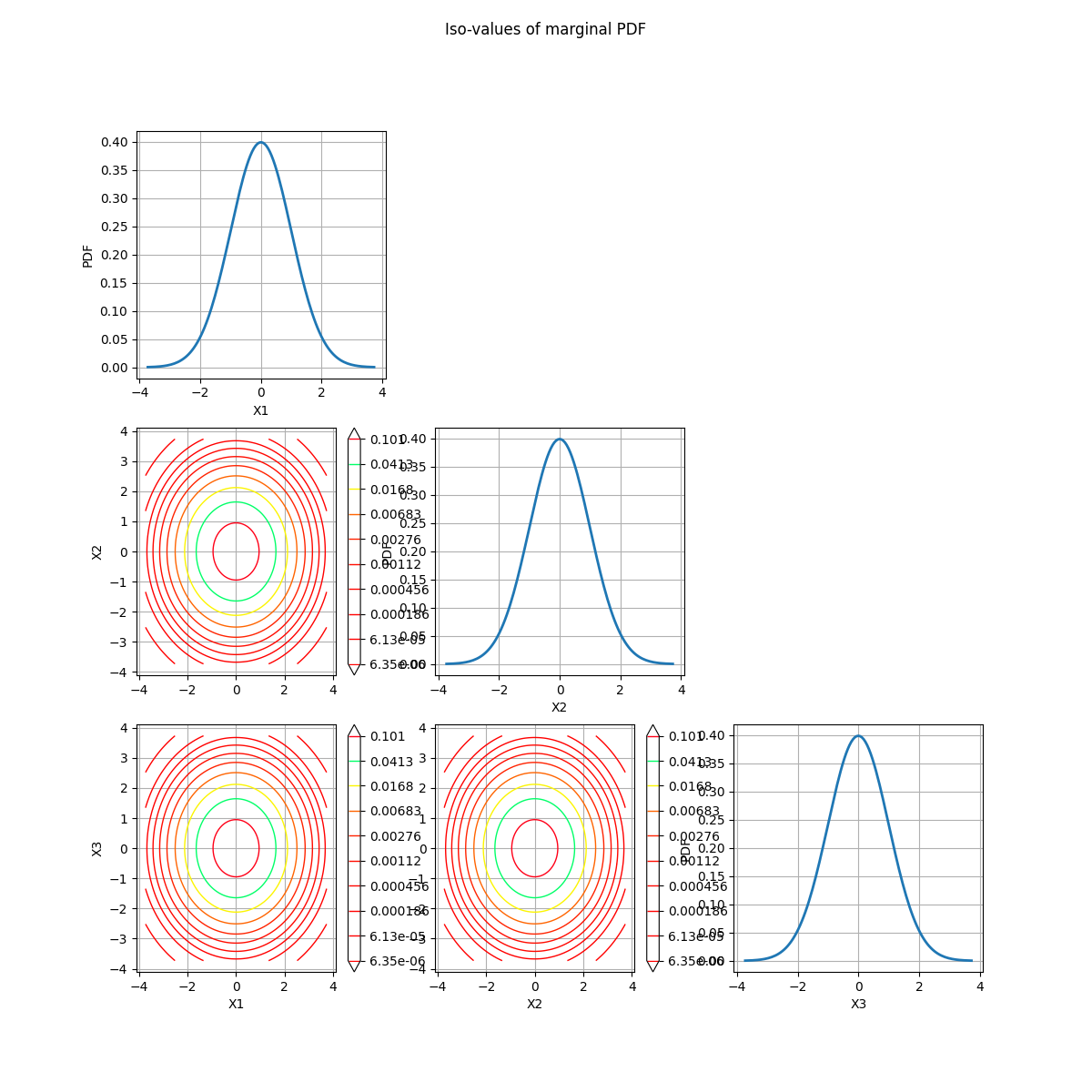
inputVector = event.getAntecedent()
event = problem.getEvent()
g = event.getFunction()

sampleSize = 5000
sampleInput = inputVector.getSample(sampleSize)
sampleOutput = g(sampleInput)
drawEvent = otb.DrawEvent(event)

_ = drawEvent.drawLimitState(bounds)

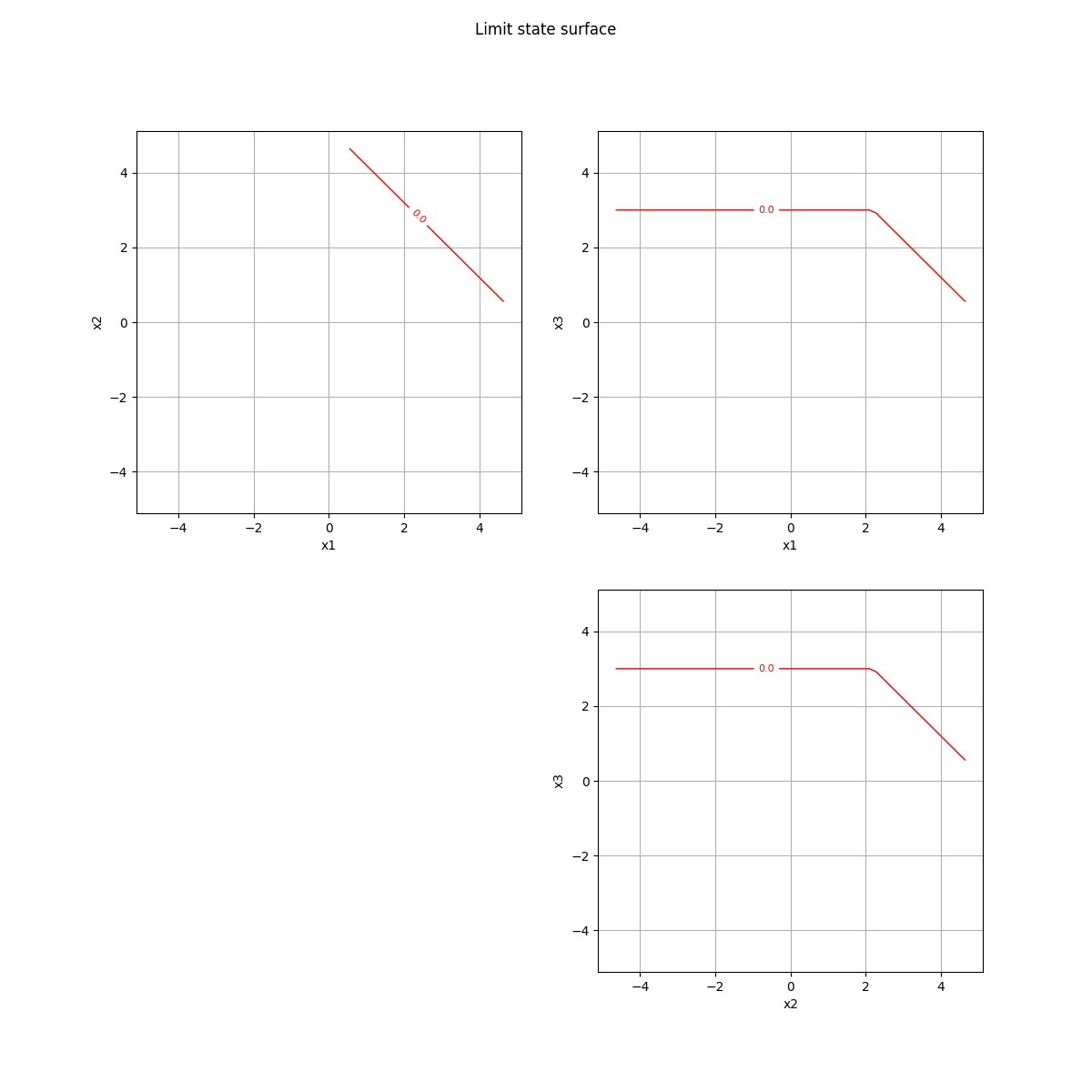
sampleSize = 500
_ = drawEvent.drawSample(sampleSize)

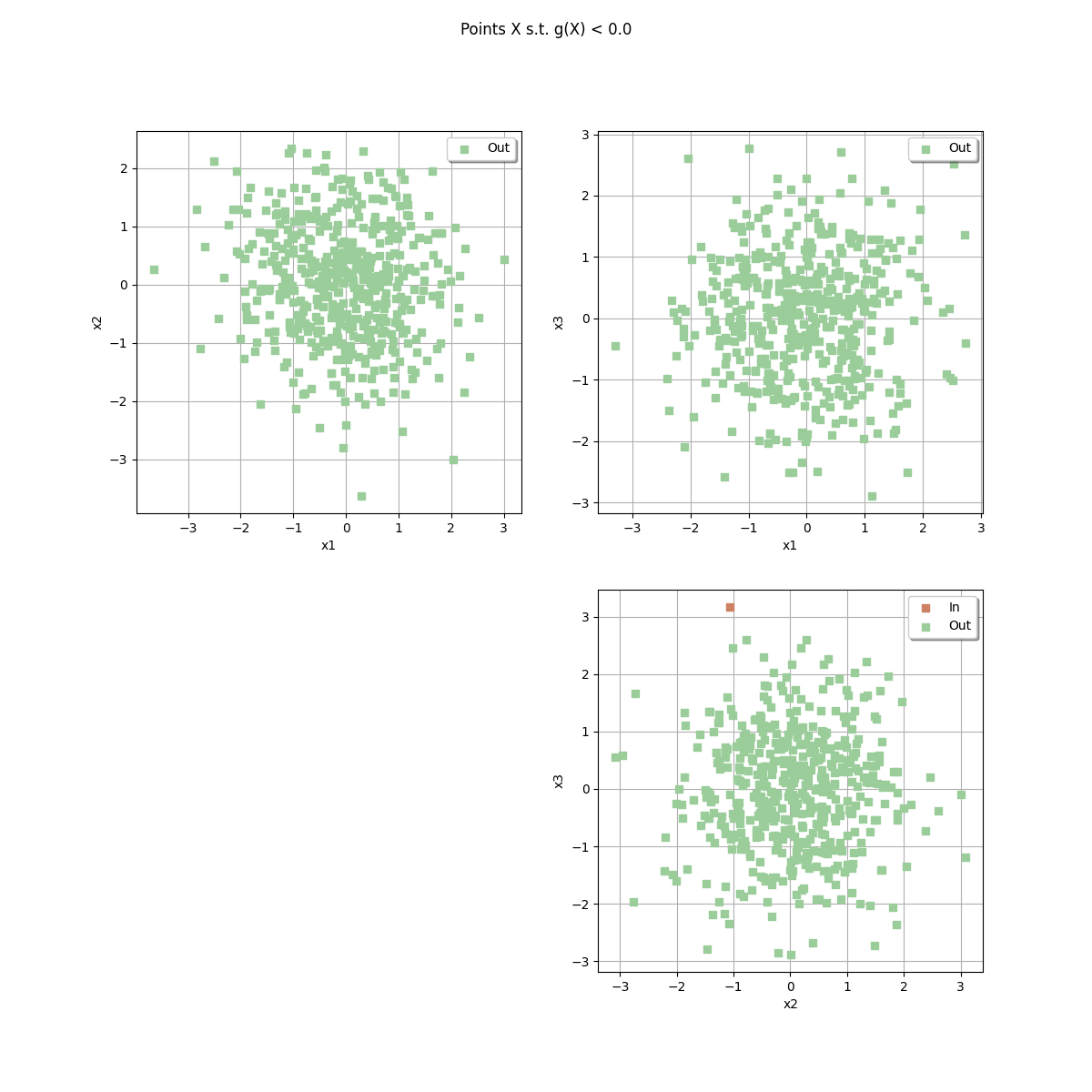
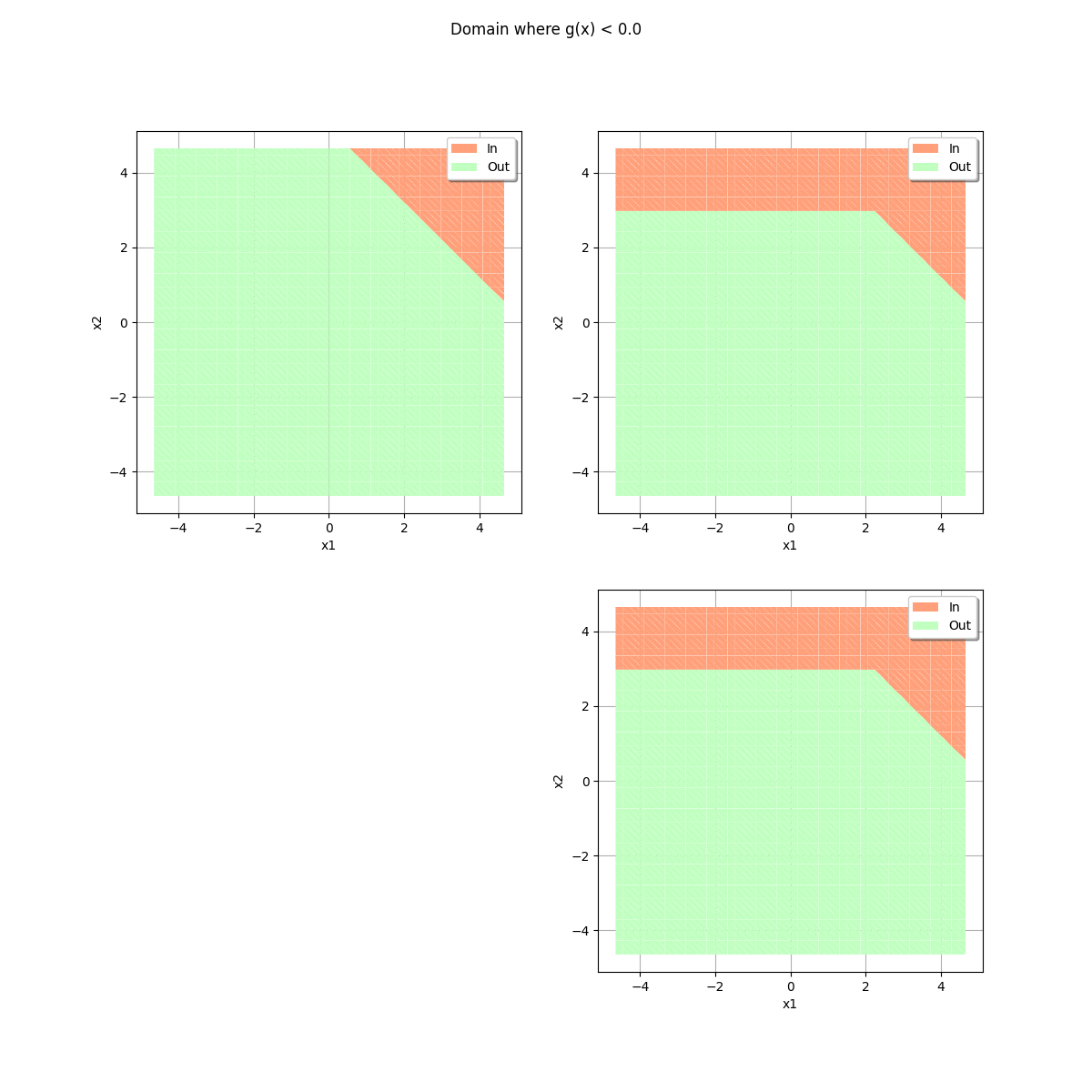
_ = drawEvent.fillEvent(bounds)