CorrelationAnalysis¶
- class CorrelationAnalysis(*args)¶
Correlation analysis methods.
Provides elementary sensitivity analysis methods to determine the influence of each component of a random vector over a single one-dimensional variable.
- Parameters:
- firstSample2-d list of float
Values taken by a random vector.
- secondSample2-d list of float
Values taken by a single one-dimensional random variable.
See also
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> firstSample = ot.Normal(3).getSample(100) >>> model = ot.SymbolicFunction(['x', 'y', 'z'], ['x + 3 * y - 5 * z']) >>> secondSample = model(firstSample) >>> correlationAnalysis = ot.CorrelationAnalysis(firstSample, secondSample) >>> cor = correlationAnalysis.computeLinearCorrelation()
Methods
Correlation evaluation based on Kendall's
coefficient.
Correlation evaluation based on the linear (Pearson) correlation coefficient.
Correlation evaluation based on the Partial Correlation Coefficient.
Correlation evaluation based on the Partial Rank Correlation Coefficient.
Correlation evaluation based on the Standard Regression Coefficient.
Correlation evaluation based on the Standard Rank Regression Coefficient.
Correlation evaluation based on the Spearman correlation coefficient.
computeSquaredSRC([normalize])Correlation evaluation based on the square of the Standard Regression Coefficient.
Accessor to the object's name.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
computePearsonCorrelation
- __init__(*args)¶
- computeKendallTau()¶
Correlation evaluation based on Kendall’s
coefficient.
See the
SamplecomputeKendallTau()method for details.- Returns:
- coef
Point Kendall’s
coefficients evaluated between the secondSample and each coordinate of the firstSample.
- coef
- computeLinearCorrelation()¶
Correlation evaluation based on the linear (Pearson) correlation coefficient.
Refer to Pearson correlation coefficient.
- Returns:
- coef
Point The linear (Pearson) coefficients evaluated between the secondSample and each coordinate of the firstSample.
- coef
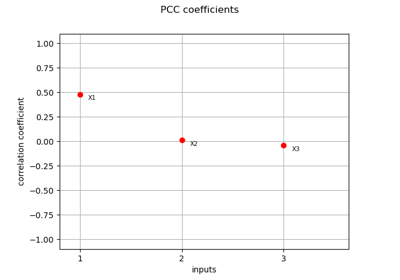
- computePCC()¶
Correlation evaluation based on the Partial Correlation Coefficient.
Refer to Uncertainty ranking: PCC and PRCC.
- Returns:
- coef
Point The PCC coefficients evaluated between the secondSample and each coordinate of the firstSample.
- coef
- computePRCC()¶
Correlation evaluation based on the Partial Rank Correlation Coefficient.
Refer to Uncertainty ranking: PCC and PRCC.
- Returns:
- coef
Point The PRCC coefficients evaluated between the secondSample and each coordinate of the firstSample.
- coef
- computeSRC()¶
Correlation evaluation based on the Standard Regression Coefficient.
Refer to Uncertainty ranking: SRC and SRRC.
- Returns:
- coef
Point The SRC evaluated between the secondSample and each coordinate of the firstSample.
- coef
- computeSRRC()¶
Correlation evaluation based on the Standard Rank Regression Coefficient.
Refer to Uncertainty ranking: SRC and SRRC.
- Returns:
- coef
Point The SRRC evaluated between the secondSample and each coordinate of the firstSample.
- coef
- computeSpearmanCorrelation()¶
Correlation evaluation based on the Spearman correlation coefficient.
Refer to Spearman correlation coefficient.
- Returns:
- coef
Point The Spearman coefficients evaluated between the secondSample and each coordinate of the firstSample.
- coef
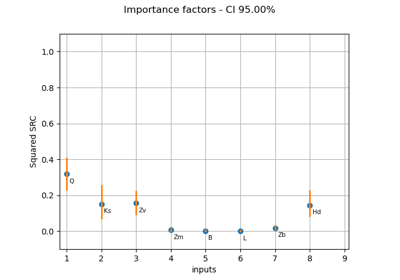
- computeSquaredSRC(normalize=False)¶
Correlation evaluation based on the square of the Standard Regression Coefficient.
Refer to Uncertainty ranking: SRC and SRRC.
- Parameters:
- normalizebool
If True, coefficients sum to one. Default value is False.
- Returns:
- coef
Point The squared SRC evaluated between the secondSample and each coordinate of the firstSample.
- coef
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
Example of sensitivity analyses on the wing weight model
 OpenTURNS
OpenTURNS