IndependentCopula¶

(Source code, png)

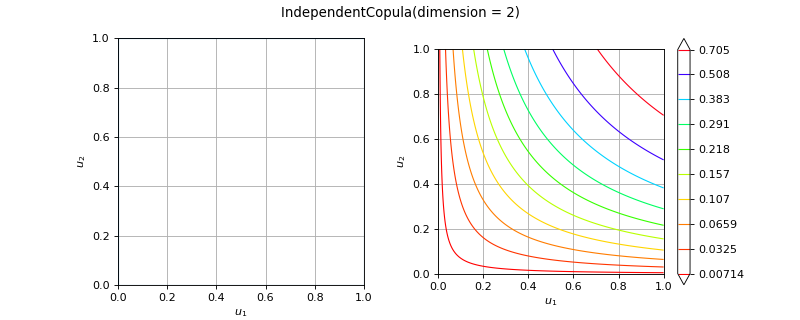
class IndependentCopula(*args)¶

Independent copula.

Parameters:

nint

Dimension of the copula, $n \geq 1$ .

Default value is 2.

See also

Distribution

Notes

The Independent copula is defined by :

$C(u_1, \cdots, u_n) = \prod_{i=1}^n u_i$

for $u_i \in [0, 1]$

Examples

Create a distribution:

>>> import openturns as ot
>>> copula = ot.IndependentCopula(3)

Draw a sample:

>>> sample = copula.getSample(5)

Methods

`abs`()	Transform distribution by absolute value function.
`acos`()	Transform distribution by arccosine function.
`acosh`()	Transform distribution by acosh function.
`asin`()	Transform distribution by arcsine function.
`asinh`()	Transform distribution by asinh function.
`atan`()	Transform distribution by arctangent function.
`atanh`()	Transform distribution by atanh function.
`cbrt`()	Transform distribution by cubic root function.
`computeBilateralConfidenceInterval`(prob)	Compute a bilateral confidence interval.
`computeBilateralConfidenceIntervalWithMarginalProbability`(prob)	Compute a bilateral confidence interval.
`computeCDF`(*args)	Compute the cumulative distribution function.
`computeCDFGradient`(point)	Compute the gradient of the cumulative distribution function.
`computeCharacteristicFunction`(*args)	Compute the characteristic function.
`computeComplementaryCDF`(*args)	Compute the complementary cumulative distribution function.
`computeConditionalCDF`(*args)	Compute the conditional cumulative distribution function.
`computeConditionalDDF`(x, y)	Compute the conditional derivative density function of the last component.
`computeConditionalPDF`(*args)	Compute the conditional probability density function.
`computeConditionalQuantile`(*args)	Compute the conditional quantile function of the last component.
`computeDDF`(*args)	Compute the derivative density function.
`computeEntropy`()	Compute the entropy of the distribution.
`computeGeneratingFunction`(*args)	Compute the probability-generating function.
`computeInverseSurvivalFunction`(point)	Compute the inverse survival function.
`computeLogCharacteristicFunction`(*args)	Compute the logarithm of the characteristic function.
`computeLogGeneratingFunction`(*args)	Compute the logarithm of the probability-generating function.
`computeLogPDF`(*args)	Compute the logarithm of the probability density function.
`computeLogPDFGradient`(*args)	Compute the gradient of the log probability density function.
`computeLowerExtremalDependenceMatrix`()	Compute the lower extremal dependence coefficients.
`computeLowerTailDependenceMatrix`()	Compute the lower tail dependence coefficients.
`computeMinimumVolumeInterval`(prob)	Compute the confidence interval with minimum volume.
`computeMinimumVolumeIntervalWithMarginalProbability`(prob)	Compute the confidence interval with minimum volume.
`computeMinimumVolumeLevelSet`(prob)	Compute the confidence domain with minimum volume.
`computeMinimumVolumeLevelSetWithThreshold`(prob)	Compute the confidence domain with minimum volume.
`computePDF`(*args)	Compute the probability density function.
`computePDFGradient`(point)	Compute the gradient of the probability density function.
`computeProbability`(interval)	Compute the interval probability.
`computeQuantile`(*args)	Compute the quantile function.
`computeRadialDistributionCDF`(radius[, tail])	Compute the cumulative distribution function of the squared radius.
`computeScalarQuantile`(prob[, tail])	Compute the quantile function for univariate distributions.
`computeSequentialConditionalCDF`(x)	Compute the sequential conditional cumulative distribution functions.
`computeSequentialConditionalDDF`(x)	Compute the sequential conditional derivative density function.
`computeSequentialConditionalPDF`(x)	Compute the sequential conditional probability density function.
`computeSequentialConditionalQuantile`(q)	Compute the conditional quantile function of the last component.
`computeSurvivalFunction`(*args)	Compute the survival function.
`computeUnilateralConfidenceInterval`(prob[, tail])	Compute a unilateral confidence interval.
`computeUnilateralConfidenceIntervalWithMarginalProbability`(...)	Compute a unilateral confidence interval.
`computeUpperExtremalDependenceMatrix`()	Compute the upper extremal dependence coefficients.
`computeUpperTailDependenceMatrix`()	Compute the upper tail dependence coefficients.
`cos`()	Transform distribution by cosine function.
`cosh`()	Transform distribution by cosh function.
`drawCDF`(*args)	Draw the cumulative distribution function.
`drawLogPDF`(*args)	Draw the graph or of iso-lines of log-probability density function.
`drawLowerExtremalDependenceFunction`()	Draw the lower extremal dependence function.
`drawLowerTailDependenceFunction`()	Draw the lower tail dependence function.
`drawMarginal1DCDF`(marginalIndex, xMin, xMax, ...)	Draw the cumulative distribution function of a margin.
`drawMarginal1DLogPDF`(marginalIndex, xMin, ...)	Draw the log-probability density function of a margin.
`drawMarginal1DPDF`(marginalIndex, xMin, xMax, ...)	Draw the probability density function of a margin.
`drawMarginal1DSurvivalFunction`(...[, logScale])	Draw the cumulative distribution function of a margin.
`drawMarginal2DCDF`(firstMarginal, ...[, ...])	Draw the cumulative distribution function of a couple of margins.
`drawMarginal2DLogPDF`(firstMarginal, ...[, ...])	Draw the log-probability density function of a couple of margins.
`drawMarginal2DPDF`(firstMarginal, ...[, ...])	Draw the probability density function of a couple of margins.
`drawMarginal2DSurvivalFunction`(...[, ...])	Draw the cumulative distribution function of a couple of margins.
`drawPDF`(*args)	Draw the graph or of iso-lines of probability density function.
`drawQuantile`(*args)	Draw the quantile function.
`drawSurvivalFunction`(*args)	Draw the cumulative distribution function.
`drawUpperExtremalDependenceFunction`()	Draw the upper extremal dependence function.
`drawUpperTailDependenceFunction`()	Draw the upper tail dependence function.
`exp`()	Transform distribution by exponential function.
`getCDFEpsilon`()	Accessor to the CDF computation precision.
`getCentralMoment`(n)	Accessor to the componentwise central moments.
`getCholesky`()	Accessor to the Cholesky factor of the covariance matrix.
`getClassName`()	Accessor to the object's name.
`getCopula`()	Accessor to the copula of the distribution.
`getCorrelation`()	Accessor to the correlation matrix.
`getCovariance`()	Accessor to the covariance matrix.
`getDescription`()	Accessor to the componentwise description.
`getDimension`()	Accessor to the dimension of the distribution.
`getDispersionIndicator`()	Dispersion indicator accessor.
`getIntegrationNodesNumber`()	Accessor to the number of Gauss integration points.
`getInverseCholesky`()	Accessor to the inverse Cholesky factor of the covariance matrix.
`getInverseIsoProbabilisticTransformation`()	Accessor to the inverse iso-probabilistic transformation.
`getIsoProbabilisticTransformation`()	Accessor to the iso-probabilistic transformation.
`getKendallTau`()	Accessor to the Kendall coefficients matrix.
`getKurtosis`()	Accessor to the componentwise kurtosis.
`getMarginal`(*args)	Accessor to marginal distributions.
`getMean`()	Accessor to the mean.
`getMoment`(n)	Accessor to the componentwise moments.
`getName`()	Accessor to the object's name.
`getPDFEpsilon`()	Accessor to the PDF computation precision.
`getParameter`()	Accessor to the parameter of the distribution.
`getParameterDescription`()	Accessor to the parameter description of the distribution.
`getParameterDimension`()	Accessor to the number of parameters in the distribution.
`getParametersCollection`()	Accessor to the parameter of the distribution.
`getPearsonCorrelation`()	Accessor to the Pearson correlation matrix.
`getPositionIndicator`()	Position indicator accessor.
`getProbabilities`()	Accessor to the discrete probability levels.
`getRange`()	Accessor to the range of the distribution.
`getRealization`()	Accessor to a pseudo-random realization from the distribution.
`getRoughness`()	Accessor to roughness of the distribution.
`getSample`(size)	Accessor to a pseudo-random sample from the distribution.
`getSampleByInversion`(size)	Accessor to a pseudo-random sample from the distribution.
`getSampleByQMC`(size)	Accessor to a low discrepancy sample from the distribution.
`getShapeMatrix`()	Accessor to the shape matrix of the underlying copula if it is elliptical.
`getShiftedMoment`(n, shift)	Accessor to the componentwise shifted moments.
`getSingularities`()	Accessor to the singularities of the PDF function.
`getSkewness`()	Accessor to the componentwise skewness.
`getSpearmanCorrelation`()	Accessor to the Spearman correlation matrix.
`getStandardDeviation`()	Accessor to the componentwise standard deviation.
`getStandardDistribution`()	Accessor to the standard distribution.
`getStandardRepresentative`()	Accessor to the standard representative distribution in the parametric family.
`getSupport`(*args)	Accessor to the support of the distribution.
`hasEllipticalCopula`()	Test whether the copula of the distribution is elliptical or not.
`hasIndependentCopula`()	Test whether the copula of the distribution is the independent one.
`hasName`()	Test if the object is named.
`inverse`()	Transform distribution by inverse function.
`isContinuous`()	Test whether the distribution is continuous or not.
`isCopula`()	Test whether the distribution is a copula or not.
`isDiscrete`()	Test whether the distribution is discrete or not.
`isElliptical`()	Test whether the distribution is elliptical or not.
`isIntegral`()	Test whether the distribution is integer-valued or not.
`ln`()	Transform distribution by natural logarithm function.
`log`()	Transform distribution by natural logarithm function.
`setDescription`(description)	Accessor to the componentwise description.
`setIntegrationNodesNumber`(integrationNodesNumber)	Accessor to the number of Gauss integration points.
`setName`(name)	Accessor to the object's name.
`setParameter`(parameters)	Accessor to the parameter of the distribution.
`setParametersCollection`(*args)	Accessor to the parameter of the distribution.
`sin`()	Transform distribution by sine function.
`sinh`()	Transform distribution by sinh function.
`sqr`()	Transform distribution by square function.
`sqrt`()	Transform distribution by square root function.
`tan`()	Transform distribution by tangent function.
`tanh`()	Transform distribution by tanh function.

__init__(*args)¶

abs()¶

Transform distribution by absolute value function.

Returns:

distDistribution: The transformed distribution.

acos()¶

Transform distribution by arccosine function.

Returns:

distDistribution: The transformed distribution.

acosh()¶

Transform distribution by acosh function.

Returns:

distDistribution: The transformed distribution.

asin()¶

Transform distribution by arcsine function.

Returns:

distDistribution: The transformed distribution.

asinh()¶

Transform distribution by asinh function.

Returns:

distDistribution: The transformed distribution.

atan()¶

Transform distribution by arctangent function.

Returns:

distDistribution: The transformed distribution.

atanh()¶

Transform distribution by atanh function.

Returns:

distDistribution: The transformed distribution.

cbrt()¶

Transform distribution by cubic root function.

Returns:

distDistribution: The transformed distribution.

computeBilateralConfidenceInterval(prob)¶

Compute a bilateral confidence interval.

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.

Returns:

confIntervalInterval: The confidence interval of level alpha.

Notes

We consider an absolutely continuous measure $\mu$ with density function $p$ .

The bilateral confidence interval $I^*_{\alpha}$ is the Cartesian product $I^*_{\alpha} = [a_1, b_1] \times \dots \times [a_d, b_d]$ such that there exists $\beta \in [0,1]$ which satisfies the equations $a_i = F_i^{-1}((1 - \beta) / 2)$ and $b_i = F_i^{-1}((1 + \beta) / 2)$ for all $i$ and $\mu(I^*_{\alpha}) = \alpha$ .

Examples

We consider a Normal(2) distribution with zero mean, unit standard deviation and independent components. We note $\Phi_2$ its cdf. Due to symetries of the distribution, the bilateral confidence interval is $I^*_{\alpha} = [-a, a] \times \times [-a, a]$ where $a = \Phi^{-1}((1+\beta)/2)$ where $\Phi$ is the marginal cdf of each component. Then $\beta$ is such that $\Phi_2(I^*_{\alpha}) = \alpha$ . As $\Phi_2(I^*_{\alpha}) = (2\Phi(a) - 1)^2 = _beta^2$ , then, $\beta$ is equal to $\beta = \sqrt{\alpha} \simeq 0.9486$ and $a \simeq -1.9488$ .

>>> import openturns as ot
>>> dist = ot.Normal(2)
>>> confInt = dist.computeBilateralConfidenceInterval(0.9)

computeBilateralConfidenceIntervalWithMarginalProbability(prob)¶

Compute a bilateral confidence interval.

Refer to computeBilateralConfidenceInterval()

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.

Returns:

confIntervalInterval: The confidence interval of level alpha.
betafloat: The probability $\beta$ .

Examples

We consider a Normal(2) distribution with zero mean, unit standard deviation and independent components. We note $\Phi_2$ its cdf. Due to symetries of the distribution, the bilateral confidence interval is $I^*_{\alpha} = [-a, a] \times [-a, a]$ where $a = \Phi^{-1}((1 + \beta) / 2)$ where $\Phi$ is the marginal cdf of each 1D marginal standard Gaussian component. Then $\beta$ is such that $\Phi_2(I^*_{\alpha}) = \alpha$ . As $\Phi_2(I^*_{\alpha}) = (2\Phi(a) - 1)^2 = \beta^2$ , then, $\beta$ is equal to $\beta = \sqrt{\alpha} = 0.9486$ and $a = -1.9488$ with 4 significant digits.

>>> import openturns as ot
>>> dist = ot.Normal(2)
>>> confInt, beta = dist.computeBilateralConfidenceIntervalWithMarginalProbability(0.9)

computeCDF(*args)¶

Compute the cumulative distribution function.

Parameters:

xsequence of float, 2-d sequence of float: Point in $\Rset^d$ .

Returns:

Ffloat, Point: CDF value at x.

Notes

The cumulative distribution function is defined as:

$F_{\vect{X}}(\vect{x}) = \Prob{\bigcap_{i=1}^n X_i \leq x_i}, \quad \vect{x} \in \Rset^d$

computeCDFGradient(point)¶

Compute the gradient of the cumulative distribution function.

Parameters:

xsequence of float: Point in $\Rset^d$ .

Returns:

dFdthetaPoint: Partial derivatives of the CDF with respect to the distribution parameters at x.

computeCharacteristicFunction(*args)¶

Compute the characteristic function.

Parameters:

tfloat: Characteristic function input.

Returns:

phicomplex: Characteristic function value at input t.

Notes

The characteristic function is defined as:

$\phi_X(t) = \mathbb{E}\left[\exp(- i t X)\right], \quad t \in \Rset$

OpenTURNS features a generic implementation of the characteristic function for all its univariate distributions (both continuous and discrete). This default implementation might be time consuming, especially as the modulus of $t$ gets high. Only some univariate distributions benefit from dedicated more efficient implementations.

computeComplementaryCDF(*args)¶

Compute the complementary cumulative distribution function.

Parameters:

xsequence of float, 2-d sequence of float: Point in $\Rset^d$ .

Returns:

Cfloat, Point: Complementary CDF value at x.

See also

computeSurvivalFunction

Notes

The complementary cumulative distribution function.

$1 - F_{\vect{X}}(\vect{x}) = 1 - \Prob{\bigcap_{i = 1}^d \left\{X_i \leq x_i \right\}}, \qquad \vect{x} \in \Rset^d$

Warning

The complementary CDF is different from the survival function (except for scalar distributions).

computeConditionalCDF(*args)¶

Compute the conditional cumulative distribution function.

Parameters:

xjfloat, sequence of float: Conditional CDF input.
xcondsequence of float, 2-d sequence of float with size $j-1$ , $j \leq d$: Conditioning values for the components $(X_{1}, \dots, X_{j-1})$ .

Returns:

pfloat, sequence of float: Conditional CDF value at xj given xcond.

Notes

Let $\vect{X}$ be a random vector of dimension $d$ . The conditional cumulative distribution function of the component $X_j$ given that the components of indices $k \leq j-1$ are fixed to $(x_1, \dots, x_{j-1})$ is defined by:

$F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) = \Prob{X_j \leq x_j \mid X_1=x_1, \ldots, X_{j-1}=x_{j-1}}.$

For $j=1$ , it reduces to $F_{X_1}(x_1)$ .

computeConditionalDDF(x, y)¶

Compute the conditional derivative density function of the last component.

With respect to the other fixed components.

Parameters:

xjfloat, sequence of float: Conditional CDF input.
xcondsequence of float, 2-d sequence of float with size $j-1$ , $j \leq d$: Conditioning values for the components $(X_{1}, \dots, X_{j-1})$ .

Returns:

ddffloat,: Conditional DDF value at xj given xcond.

See also

computeDDF, computeConditionalCDF

Notes

Let $\vect{X}$ be a random vector of dimension $d$ . The conditional derivative density function of the component $X_j$ given that the components of indices $k \leq j-1$ are fixed to $(x_1, \dots, x_{j-1})$ is defined by:

$\dfrac{d^2}{d\,x_j^2}F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1})$

where for $2 \leq j \leq d$ :

$F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) = \Prob{X_j \leq x_j \mid X_1=x_1, \ldots, X_{j-1}=x_{j-1}}.$

For $j=1$ , it reduces to $\dfrac{d^2}{d\,x_1^2}F_{X_1}(x_1)$ , ie the DDF of the first component at $x_1$ .

computeConditionalPDF(*args)¶

Compute the conditional probability density function.

Conditional PDF of the last component with respect to the other fixed components.

Parameters:

xjfloat, sequence of float,: Conditional CDF input.
xcondsequence of float, 2-d sequence of float with size $j-1$ , $j \leq d$: Conditioning values for the components $(X_{1}, \dots, X_{j-1})$ .

Returns:

cpdffloat, sequence of float: Conditional PDF at xd, given xcond.

See also

computePDF, computeConditionalCDF

Notes

Let $\vect{X}$ be a random vector of dimension $d$ . The conditional probability density function of the component $X_j$ given that the components of indices $k \leq j-1$ are fixed to $(x_1, \dots, x_{j-1})$ is defined by:

$\dfrac{d}{d\,x_j}F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1})$

where for $2 \leq j \leq d$ :

$F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) = \Prob{X_j \leq x_j \mid X_1=x_1, \ldots, X_{j-1}=x_{j-1}}.$

For $j=1$ , it reduces to $\dfrac{d}{d\,x_1}F_{X_1}(x_1)$ .

computeConditionalQuantile(*args)¶

Compute the conditional quantile function of the last component.

Conditional quantile with respect to the other fixed components.

Parameters:

pfloat, sequence of float, $p \in [0, 1]$: Conditional quantile.
xcondsequence of float, 2-d sequence of float with size $j-1$ , $j \leq d$: Conditioning values for the components $(X_{1}, \dots, X_{j-1})$ .

Returns:

xjfloat: Conditional quantile of order p of the component $X_j$ given that the components of indices $k \leq j-1$ are fixed and equal to xcond.

See also

computeQuantile, computeConditionalCDF

Notes

Let $\vect{X}$ be a random vector of dimension $d$ . The conditional quantile of order $p$ of the component $X_j$ given that the components of indices $k \leq j-1$ are fixed to $(x_1, \dots, x_{j-1})$ is defined by:

$F^{-1}_{X_j \mid X_1, \ldots, X_{j - 1}}(p; x_1, \dots, x_{j-1})$

where $F^{-1}$ is the quantile function. For $j=1$ , it reduces to $F^{-1}_{X_1}(p)$ .

computeDDF(*args)¶

Compute the derivative density function.

Parameters:

xsequence of float, 2-d sequence of float: The input value where the conditional derivative density function must be evaluated.

Returns:

ddfPoint, Sample: DDF value at x.

Notes

The derivative density function is the gradient of the probability density function with respect to $\vect{x}$ :

$\vect{\nabla}_{\vect{x}} f_{\vect{X}}(\vect{x}) = \Tr{\left(\frac{\partial f_{\vect{X}}(\vect{x})}{\partial x_1}, \dots, \frac{\partial f_{\vect{X}}(\vect{x})}{\partial x_d}\right)}, \quad \vect{x} \in \Rset^d$

computeEntropy()¶

Compute the entropy of the distribution.

Returns:

efloat: Entropy of the distribution.

Notes

The entropy of a distribution is defined by:

$\cE_X = \Expect{-\log(p_X(\vect{X}))}$

Where the random vector $\vect{X}$ follows the probability distribution of interest, and $p_X$ is either the probability density function of $\vect{X}$ if it is continuous or the probability distribution function if it is discrete.

computeGeneratingFunction(*args)¶

Compute the probability-generating function.

Parameters:

zfloat or complex: Probability-generating function input.

Returns:

gfloat: Probability-generating function value at input z.

See also

isDiscrete

Notes

The probability-generating function is defined as follows:

$G_X(z) = \Expect{z^X}, \quad z \in \Cset$

This function only exists for discrete distributions. OpenTURNS implements this method for univariate distributions only.

computeInverseSurvivalFunction(point)¶

Compute the inverse survival function.

Parameters:

pfloat, $p \in [0; 1]$: Value of the survival function.

Returns:

xPoint: Point $\vect{x}$ such that $S_{\vect{X}}(\vect{x}) = p$ with iso-quantile components.

See also

computeQuantile, computeSurvivalFunction

Notes

Among the points $\vect{x}$ that satisfy $S_{\vect{X}}(\vect{x}) = p$ , the method returns the one which also satisfies $\Prob{X_1 > x_1} = \dots = \Prob{X_d > x_d}$ .

computeLogCharacteristicFunction(*args)¶

Compute the logarithm of the characteristic function.

Parameters:

tfloat: Characteristic function input.

Returns:

phicomplex: Logarithm of the characteristic function value at input t.

See also

computeCharacteristicFunction

Notes

OpenTURNS features a generic implementation of the characteristic function for all its univariate distributions (both continuous and discrete). This default implementation might be time consuming, especially as the modulus of $t$ gets high. Only some univariate distributions benefit from dedicated more efficient implementations.

computeLogGeneratingFunction(*args)¶

Compute the logarithm of the probability-generating function.

Parameters:

zfloat or complex: Probability-generating function input.

Returns:

lgfloat: Logarithm of the probability-generating function value at input z.

See also

isDiscrete, computeGeneratingFunction

Notes

This function only exists for discrete distributions. OpenTURNS implements this method for univariate distributions only.

computeLogPDF(*args)¶

Compute the logarithm of the probability density function.

Parameters:

xsequence of float, 2-d sequence of float: Point in $\Rset^d$ such that the PDF at this point is non equal to 0.

Returns:

ffloat, Point: Logarithm of the PDF at x.

computeLogPDFGradient(*args)¶

Compute the gradient of the log probability density function.

Parameters:

xsequence of float: Point in $\Rset^d$ .

Returns:

dfdthetaPoint: Partial derivatives of the logPDF with respect to the distribution parameters at input x.

computeLowerExtremalDependenceMatrix()¶

Compute the lower extremal dependence coefficients.

We assume that the distribution is $d$ -dimensional, with $d \geq 2$ and that its copula is denoted by $C$ . The lower extremal dependence matrix is $(\bar{\chi}_L^{ij})_{1 \leq i, j \leq d}$ where $\\bar{\chi}_L^{ij}$ is the lower extremal dependence coefficient of the bivariate distribution $(X_i, X_j)$ . It is defined by:

$\bar{\chi}_L^{ij} = \lim_{u \to 0} \bar{\chi}_L^{ij}(u)$

where $u \mapsto \bar{\chi}_L^{ij}(u)$ is the lower extremal dependence function of the bivariate distribution $(X_i, X_j)$ defined by:

$\bar{\chi}_L(u) = \frac{2 \log u}{\log C(u,u)} - 1, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

depCorrelationMatrix: The dependence matrix.

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> chiLb = copula.computeLowerExtremalDependenceMatrix()[1, 0]

computeLowerTailDependenceMatrix()¶

Compute the lower tail dependence coefficients.

We assume that the distribution is $d$ -dimensional, with $d \geq 2$ and that its copula is denoted by $C$ . The lower tail dependence matrix is $(\chi_L^{ij})_{1 \leq i, j \leq d}$ where $\chi_L^{ij}$ is the lower tail dependence coefficient of the bivariate distribution $(X_i, X_j)$ . It is defined by:

$\chi_L^{ij} = \lim_{u \to 0} \chi_L^{ij}(u)$

where $u \mapsto \chi_L^{ij}(u)$ is the lower tail dependence function of the bivariate distribution $(X_i, X_j)$ defined by:

$\chi_L(u) = \frac{\log (1 - C(u,u))}{\log (1-u)}, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

depCorrelationMatrix: The dependence matrix.

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> chiL = copula.computeLowerTailDependenceMatrix()[1, 0]

computeMinimumVolumeInterval(prob)¶

Compute the confidence interval with minimum volume.

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.

Returns:

confIntervalInterval: The confidence interval of level alpha.

Notes

We consider an absolutely continuous measure $\mu$ with density function $p$ .

The minimum volume confidence interval $I^*_{\alpha}$ is the Cartesian product $I^*_{\alpha} = [a_1, b_1] \times \dots \times [a_d, b_d]$ where $[a_i, b_i] = \argmin_{I \in \Rset \, | \, \mu_i(I) = \beta} \lambda_i(I)$ and $\mu(I^*_{\alpha}) = \alpha$ with $\lambda$ is the Lebesgue measure on $\Rset^d$ .

This problem resorts to solving $d$ univariate non linear equations: for a fixed value $\beta$ , we find each intervals $[a_i, b_i]$ such that:

$\begin{eqnarray*} F_i(b_i) - F_i(a_i) & = & \beta \\ p_i(b_i) & = & p_i(a_i) \end{eqnarray*}$

which consists of finding the bound $a_i$ such that:

$p_i(a_i) = p_i(F_i^{-1}(\beta + F_i(a_i)))$

To find $\beta$ , we use the Brent algorithm: $\mu([\vect{a}(\beta); \vect{b}(\beta)] = g(\beta) = \alpha$ with $g$ a non linear function.

Examples

Create a sample from a Normal distribution:

>>> import openturns as ot
>>> sample = ot.Normal().getSample(10)
>>> ot.ResourceMap.SetAsUnsignedInteger('DistributionFactory-DefaultBootstrapSize', 100)

Fit a Normal distribution and extract the asymptotic parameters distribution:

>>> fittedRes = ot.NormalFactory().buildEstimator(sample)
>>> paramDist = fittedRes.getParameterDistribution()

Determine the confidence interval of the native parameters at level 0.9 with minimum volume:

>>> ot.ResourceMap.SetAsUnsignedInteger('Distribution-MinimumVolumeLevelSetSamplingSize', 1000)
>>> confInt = paramDist.computeMinimumVolumeInterval(0.9)
>>> ot.ResourceMap.Reload()

computeMinimumVolumeIntervalWithMarginalProbability(prob)¶

Compute the confidence interval with minimum volume.

Refer to computeMinimumVolumeInterval()

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.

Returns:

confIntervalInterval: The confidence interval of level alpha.
marginalProbfloat: The value $\beta$ which is the common marginal probability of each marginal interval.

Examples

Create a sample from a Normal distribution:

>>> import openturns as ot
>>> sample = ot.Normal().getSample(10)
>>> ot.ResourceMap.SetAsUnsignedInteger('DistributionFactory-DefaultBootstrapSize', 100)

Fit a Normal distribution and extract the asymptotic parameters distribution:

>>> fittedRes = ot.NormalFactory().buildEstimator(sample)
>>> paramDist = fittedRes.getParameterDistribution()

Determine the confidence interval of the native parameters at level 0.9 with minimum volume:

>>> ot.ResourceMap.SetAsUnsignedInteger('Distribution-MinimumVolumeLevelSetSamplingSize', 1000)
>>> confInt, marginalProb = paramDist.computeMinimumVolumeIntervalWithMarginalProbability(0.9)
>>> ot.ResourceMap.Reload()

computeMinimumVolumeLevelSet(prob)¶

Compute the confidence domain with minimum volume.

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.

Returns:

levelSetLevelSet: The minimum volume domain of measure alpha.

Notes

We consider an absolutely continuous measure $\mu$ with density function $p$ .

The minimum volume confidence domain $A^*_{\alpha}$ is the set of minimum volume and which measure is at least $\alpha$ . It is defined by:

$A^*_{\alpha} = \argmin_{A \in \Rset^d\, | \, \mu(A) \geq \alpha} \lambda(A)$

where $\lambda$ is the Lebesgue measure on $\Rset^d$ . Under some general conditions on $\mu$ (for example, no flat regions), the set $A^*_{\alpha}$ is unique and realises the minimum: $\mu(A^*_{\alpha}) = \alpha$ . We show that $A^*_{\alpha}$ writes:

$A^*_{\alpha} = \{ \vect{x} \in \Rset^d \, | \, p(\vect{x}) \geq p_{\alpha} \}$

for a certain $p_{\alpha} >0$ .

If we consider the random variable $Y = p(\vect{X})$ , with cumulative distribution function $F_Y$ , then $p_{\alpha}$ is defined by:

$1-F_Y(p_{\alpha}) = \alpha$

Thus the minimum volume domain of confidence $\alpha$ is the interior of the domain which frontier is the $1-\alpha$ quantile of $Y$ . It can be determined with simulations of $Y$ .

Examples

Create a sample from a Normal distribution:

>>> import openturns as ot
>>> sample = ot.Normal().getSample(10)
>>> ot.ResourceMap.SetAsUnsignedInteger('DistributionFactory-DefaultBootstrapSize', 100)

Fit a Normal distribution and extract the asymptotic parameters distribution:

>>> fittedRes = ot.NormalFactory().buildEstimator(sample)
>>> paramDist = fittedRes.getParameterDistribution()

Determine the confidence region of minimum volume of the native parameters at level 0.9:

>>> levelSet = paramDist.computeMinimumVolumeLevelSet(0.9)
>>> ot.ResourceMap.Reload()

computeMinimumVolumeLevelSetWithThreshold(prob)¶

Compute the confidence domain with minimum volume.

Refer to computeMinimumVolumeLevelSet()

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.

Returns:

levelSetLevelSet: The minimum volume domain of measure alpha.
levelfloat: The value $p_{\alpha}$ of the density function defining the frontier of the domain.

Examples

Create a sample from a Normal distribution:

>>> import openturns as ot
>>> sample = ot.Normal().getSample(10)
>>> ot.ResourceMap.SetAsUnsignedInteger('DistributionFactory-DefaultBootstrapSize', 100)

Fit a Normal distribution and extract the asymptotic parameters distribution:

>>> fittedRes = ot.NormalFactory().buildEstimator(sample)
>>> paramDist = fittedRes.getParameterDistribution()

Determine the confidence region of minimum volume of the native parameters at level 0.9 with PDF threshold:

>>> levelSet, threshold = paramDist.computeMinimumVolumeLevelSetWithThreshold(0.9)

computePDF(*args)¶

Compute the probability density function.

Parameters:

xsequence of float, 2-d sequence of float: Point in $\Rset^d$ .

Returns:

ffloat, Point: PDF value at x.

Notes

The probability density function is defined as follows:

$f_{\vect{X}}(\vect{x}) = \frac{\partial^d F_{\vect{X}}(\vect{x})} {\prod_{i=1}^d \partial x_i}, \quad \vect{x} \in \Rset^d$

computePDFGradient(point)¶

Compute the gradient of the probability density function.

Parameters:

xsequence of float: Point in $\Rset^d$ .

Returns:

dfdthetaPoint: Partial derivatives of the PDF with respect to the distribution parameters at input x.

Notes

Let $\vect{\theta}$ be the vector of parameters of the distribution. Then the gradient of the probability density function $f_{\vect{X}}$ is defined by:

$(\frac{\partial f_{\vect{X}}(\vect{x})}{\partial x_1}, \dots, \frac{\partial f_{\vect{X}}(\vect{x})}{\partial x_d})$

computeProbability(interval)¶

Compute the interval probability.

Parameters:

intervalInterval: An interval in $\Rset^d$ .

Returns:

pfloat: The probability of interval.

Notes

This computes the probability that the random vector $\vect{X}$ lies in $interval$ .

If the interval is rectangular, i.e. if $I = \bigcap\limits_{i=1}^d [a_i, b_i]$ , then we have:

$\Prob{\vect{X} \in I} = \sum\limits_{\vect{c}} (-1)^{n(\vect{c})} F_{\vect{X}}\left(\vect{c}\right)$

where the sum runs over the $2^d$ vectors such that $\vect{c} = \Tr{(c_i, i = 1, \ldots, d)}$ with $c_i \in \{a_i, b_i\}$ , and $n(\vect{c})$ is the number of components in $\vect{c}$ such that $c_i = a_i$ .

computeQuantile(*args)¶

Compute the quantile function.

Parameters:

pfloat (or sequence of float), $p \in [0, 1]$: A probability.
tailbool, optional: True indicates that the order considered is $1-p$ . Default value is False.

Returns:

xpPoint (or Sample): If tail=False, the quantile of order $p$ . If tail=True, the quantile of order $1-p$ .

Notes

If the underlying variable $X$ is scalar, then the quantile of order $p$ , denoted by $x_p$ , is defined as the generalized inverse of its cumulative distribution function:

$x_p = F_X^{-1}(p) = \inf \{ x \in \Rset\, |\, F(x) \geq p \}, \quad 0 \leq p \leq 1.$

If the distribution is scalar and discrete, then the quantile of order $p=0$ is defined by:

$x_0 = \sup \{ x \in \Rset \, |\, F(x) = 0 \}.$

If the underlying variable $\vect{X} = (X_1, \dots, X_d)$ is of dimension $d>1$ , then the quantile of order $p$ , denoted by $\vect{x}_p \in \Rset^d$ , is such that:

$\begin{aligned} F_{\vect{X}}(\vect{x}_p) & = p \\ F_{X_i}(\vect{x}_{p,i}) & = F_{X_j}(\vect{x}_{p,j}) \quad \forall (i,j) \end{aligned}$

where $F_{X_i}$ is the $i$ -th marginal cdf. The last condition means that the quantile of order $p$ is such that all the components are associated to the same order of quantile of their margin.

computeRadialDistributionCDF(radius, tail=False)¶

Compute the cumulative distribution function of the squared radius.

For the underlying standard spherical distribution (for elliptical distributions only).

Parameters:

r2float, $0 \leq R^2$: Squared radius.

Returns:

Ffloat: CDF value at input r2.

Notes

This is the CDF of the sum of the squared independent, standard, identically distributed components:

$R^2 = \sqrt{\sum\limits_{i=1}^n U_i^2}$

computeScalarQuantile(prob, tail=False)¶

Compute the quantile function for univariate distributions.

Parameters:

pfloat, $p \in [0; 1]$: A probability.

Returns:

xpfloat: Quantile of order p.

See also

computeQuantile

Notes

The quantile of order $p$ , denoted by $x_p$ , is defined as the generalized inverse of its cumulative distribution function:

$x_p = F_X^{-1}(p) = \inf \{ x \in \Rset \, |\, F(x) \geq p \}, \quad 0 \leq p \leq 1.$

If the distribution is discrete, then the quantile of order $p=0$ is defined by:

$x_0 = \sup \{ x \in \Rset \, |\, F(x)= 0 \}.$

computeSequentialConditionalCDF(x)¶

Compute the sequential conditional cumulative distribution functions.

Parameters:

xsequence of float, with size $d$: Values to be taken sequentially as argument and conditioning part of the CDF.

Returns:

Fsequence of float: Conditional CDF values at x.

Notes

The sequential conditional cumulative distribution function is defined as follows:

$\left(F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1})\right)_{j=1,\ldots,d}$

where for $2 \leq j \leq d$ :

$F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) = \Prob{X_j \leq x_j \mid X_1=x_1, \ldots, X_{j-1}=x_{j-1}}.$

The first term, for $j=1$ , is $F_{X_1}(x_1)$ .

computeSequentialConditionalDDF(x)¶

Compute the sequential conditional derivative density function.

Parameters:

xsequence of float, with size $d$: Values to be taken sequentially as argument and conditioning part of the DDF.

Returns:

ddfsequence of float: Conditional DDF values at x.

Notes

The sequential conditional derivative density function is defined by:

$\left(\dfrac{d^2}{d\,x_j^2}F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) \right)_{j=1,\ldots,d}$

where for $2 \leq j \leq d$ :

$F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) = \Prob{X_j \leq x_j \mid X_1=x_1, \ldots, X_{j-1}=x_{j-1}}.$

The first term, for $j=1$ , is $\dfrac{d^2}{d\,x_1^2}F_{X_1}(x_1)$ .

computeSequentialConditionalPDF(x)¶

Compute the sequential conditional probability density function.

Parameters:

xsequence of float, with size $d$: Values to be taken sequentially as argument and conditioning part of the PDF.

Returns:

pdfsequence of float: Sequence of conditional PDF values at x.

Notes

The sequential conditional density function is defined as follows:

$\left(\dfrac{d}{d\,x_j}F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1})\right)_{j=1,\ldots,d}$

where for $2 \leq j \leq d$ :

$F_{X_j \mid X_1, \ldots, X_{j - 1}}(x_j; x_1, \dots, x_{j-1}) = \Prob{X_j \leq x_j \mid X_1=x_1, \ldots, X_{j-1}=x_{j-1}}.$

The first term, for $j=1$ , is $\dfrac{d}{d\,x_1}F_{X_1}(x_1)$ .

computeSequentialConditionalQuantile(q)¶

Compute the conditional quantile function of the last component.

Parameters:

psequence of float in $[0,1]$ , with size $d$: Values to be taken sequentially as the argument of the conditional quantile.

Returns:

Qsequence of float: Sequence of conditional quantiles values at p

Notes

The sequential conditional quantile function is defined by:

$\left(F^{-1}_{X_j \mid X_1, \ldots, X_{j - 1}}(p_j; x_1, \dots, x_{j-1})\right)_{i=1,\ldots,d}$

where $F^{-1}$ is the quantile function and where $x_1,\ldots,x_{j-1}$ are defined recursively as $x_1=F_1^{-1}(p_1)$ and for $2\leq j \leq d$ , $x_j=F_{X_j}^{-1}(p_j|X_1=x_1,\ldots,X_{j-1}=x_{j-1})$ : the conditioning part is the set of already computed conditional quantiles.

computeSurvivalFunction(*args)¶

Compute the survival function.

Parameters:

xsequence of float, 2-d sequence of float: Point in $\Rset^d$ .

Returns:

sfloat, Point: Value of the survival function at point x.

See also

computeComplementaryCDF

Notes

The survival function of the random vector $\vect{X}$ of dimension $d$ is defined as follows:

$S_{\vect{X}}(\vect{x}) = \Prob{\bigcap_{i = 1}^d \left\{X_i > x_i \right\}}, \qquad \vect{x} \in \Rset^d$

Warning

This is not the complementary cumulative distribution function except for scalar distributions.

computeUnilateralConfidenceInterval(prob, tail=False)¶

Compute a unilateral confidence interval.

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.
tailboolean: True indicates the interval is bounded by an lower value. False indicates the interval is bounded by an upper value. Default value is False.

Returns:

confIntervalInterval: The unilateral confidence interval of level $\alpha$ .

Notes

We consider an absolutely continuous measure $\mu$ .

The left unilateral confidence interval $I^*_{\alpha}$ is the cartesian product $I^*_{\alpha} = ]-\infty, b_1] \times \dots \times ]-\infty, b_d]$ where $b_i = F_i^{-1}(\beta)$ for all $i$ and which verifies $\mu(I^*_{\alpha}) = \alpha$ . It means that $\vect{b}$ is the quantile of level $\alpha$ of the measure $\mu$ , with iso-quantile components.

The right unilateral confidence interval $I^*_{\alpha}$ is the cartesian product $I^*_{\alpha} = ]a_1; +\infty[ \times \dots \times ]a_d; +\infty[$ where $a_i = F_i^{-1}(1-\beta)$ for all $i$ and which verifies $\mu(I^*_{\alpha}) = \alpha$ . It means that $S_{\mu}^{-1}(\vect{a}) = \alpha$ with iso-quantile components, where $S_{\mu}$ is the survival function of the measure $\mu$ .

Examples

Create a sample from a Normal distribution:

>>> import openturns as ot
>>> sample = ot.Normal().getSample(10)
>>> ot.ResourceMap.SetAsUnsignedInteger('DistributionFactory-DefaultBootstrapSize', 100)

Fit a Normal distribution and extract the asymptotic parameters distribution:

>>> fittedRes = ot.NormalFactory().buildEstimator(sample)
>>> paramDist = fittedRes.getParameterDistribution()

Determine the right unilateral confidence interval at level 0.9:

>>> confInt = paramDist.computeUnilateralConfidenceInterval(0.9)

Determine the left unilateral confidence interval at level 0.9:

>>> confInt = paramDist.computeUnilateralConfidenceInterval(0.9, True)

computeUnilateralConfidenceIntervalWithMarginalProbability(prob, tail)¶

Compute a unilateral confidence interval.

Refer to computeUnilateralConfidenceInterval()

Parameters:

alphafloat, $\alpha \in [0,1]$: The confidence level.
tailboolean: True indicates the interval is bounded by an lower value. False indicates the interval is bounded by an upper value. Default value is False.

Returns:

confIntervalInterval: The unilateral confidence interval of level alpha.
marginalProbfloat: The value $\beta$ which is the common marginal probability of each marginal interval.

Examples

Create a sample from a Normal distribution:

>>> import openturns as ot
>>> sample = ot.Normal().getSample(10)
>>> ot.ResourceMap.SetAsUnsignedInteger('DistributionFactory-DefaultBootstrapSize', 100)

Fit a Normal distribution and extract the asymptotic parameters distribution:

>>> fittedRes = ot.NormalFactory().buildEstimator(sample)
>>> paramDist = fittedRes.getParameterDistribution()

Determine the right unilateral confidence interval at level 0.9:

>>> confInt, marginalProb = paramDist.computeUnilateralConfidenceIntervalWithMarginalProbability(0.9, False)

Determine the left unilateral confidence interval at level 0.9:

>>> confInt, marginalProb = paramDist.computeUnilateralConfidenceIntervalWithMarginalProbability(0.9, True)
>>> ot.ResourceMap.Reload()

computeUpperExtremalDependenceMatrix()¶

Compute the upper extremal dependence coefficients.

We assume that the distribution is $d$ -dimensional, with $d \geq 2$ and that its copula is denoted by $C$ . The upper extremal dependence matrix is $(\bar{\chi}^{ij})_{1 \leq i, j \leq d}$ where $\bar{\chi}^{ij}$ is the upper extremal dependence coefficient of the bivariate distribution $(X_i, X_j)$ . It is defined by:

$\bar{\chi}^{ij} = \lim_{u \to 1} \bar{\chi}^{ij}(u)$

where $u \mapsto \bar{\chi}^{ij}(u)$ is the upper extremal dependence function of the bivariate distribution $(X_i, X_j)$ defined by:

$\bar{\chi}(u) = \frac{2 \log 1-u}{\log \bar{C}(u,u)} - 1, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

depCorrelationMatrix: The dependence matrix.

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> chib = copula.computeUpperExtremalDependenceMatrix()[1, 0]

computeUpperTailDependenceMatrix()¶

Compute the upper tail dependence coefficients.

We assume that the distribution is $d$ -dimensional, with $d \geq 2$ and that its copula is denoted by $C$ . The upper tail dependence matrix is $(\chi^{ij})_{1 \leq i, j \leq d}$ where $\chi^{ij}$ is the upper tail dependence coefficient of the bivariate distribution $(X_i, X_j)$ . It is defined by:

$\chi^{ij} = \lim_{u \to 1} \chi^{ij}(u)$

where $u \mapsto \chi^{ij}(u)$ is the upper tail dependence function of the bivariate distribution $(X_i, X_j)$ defined by:

$\chi(u) = 2 - \frac{\log C(u,u)}{\log u}, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

depCorrelationMatrix: The dependence matrix.

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> chi = copula.computeUpperTailDependenceMatrix()[1, 0]

cos()¶

Transform distribution by cosine function.

Returns:

distDistribution: The transformed distribution.

cosh()¶

Transform distribution by cosh function.

Returns:

distDistribution: The transformed distribution.

drawCDF(*args)¶

Draw the cumulative distribution function.

Available constructors:

drawCDF(x_min, x_max, pointNumber, logScale)

drawCDF(lowerCorner, upperCorner, pointNbrInd, logScaleX, logScaleY)

drawCDF(lowerCorner, upperCorner)

Parameters:

xMinfloat, optional: The min-value of the mesh of the x-axis. Defaults uses the quantile associated to the probability level Distribution-QMin from the ResourceMap.
xMaxfloat, optional, xMax > xMin: The max-value of the mesh of the y-axis. Defaults uses the quantile associated to the probability level Distribution-QMax from the ResourceMap.
pointNumberint: The number of points that is used for meshing each axis. Defaults uses DistributionImplementation-DefaultPointNumber from the ResourceMap.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.
lowerCornersequence of float, of dimension 2, optional: The lower corner $[x_{min}, y_{min}]$ .
upperCornersequence of float, of dimension 2, optional: The upper corner $[x_{max}, y_{max}]$ .
pointNbrIndIndices, of dimension 2: Number of points that is used for meshing each axis.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the CDF.

See also

openturns.Distribution.computeCDF
openturns.viewer.View
openturns.ResourceMap

Notes

Only valid for univariate and bivariate distributions.

Examples

View the CDF of a univariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal()
>>> graph = dist.drawCDF()
>>> graph.setLegends(['normal cdf'])

View the iso-lines CDF of a bivariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal(2)
>>> graph2 = dist.drawCDF()
>>> graph2.setLegends(['iso- normal cdf'])
>>> graph3 = dist.drawCDF([-10, -5],[5, 10], [511, 511])

drawLogPDF(*args)¶

Draw the graph or of iso-lines of log-probability density function.

Available constructors:

drawLogPDF(x_min, x_max, pointNumber, logScale)

drawLogPDF(lowerCorner, upperCorner, pointNbrInd, logScaleX, logScaleY)

drawLogPDF(lowerCorner, upperCorner)

Parameters:

xMinfloat, optional: The min-value of the mesh of the x-axis. Defaults uses the quantile associated to the probability level Distribution-QMin from the ResourceMap.
xMaxfloat, optional, xMax > xMin: The max-value of the mesh of the y-axis. Defaults uses the quantile associated to the probability level Distribution-QMax from the ResourceMap.
pointNumberint: The number of points that is used for meshing each axis. Defaults uses DistributionImplementation-DefaultPointNumber from the ResourceMap.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.
lowerCornersequence of float, of dimension 2, optional: The lower corner $[x_{min}, y_{min}]$ .
upperCornersequence of float, of dimension 2, optional: The upper corner $[x_{max}, y_{max}]$ .
pointNbrIndIndices, of dimension 2: Number of points that is used for meshing each axis.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the log-PDF or its iso_lines.

See also

openturns.Distribution.computeLogPDF
openturns.viewer.View
openturns.ResourceMap

Notes

Only valid for univariate and bivariate distributions.

Examples

View the log-PDF of a univariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal()
>>> graph = dist.drawLogPDF()
>>> graph.setLegends(['normal log-pdf'])

View the iso-lines log-PDF of a bivariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal(2)
>>> graph2 = dist.drawLogPDF()
>>> graph2.setLegends(['iso- normal pdf'])
>>> graph3 = dist.drawLogPDF([-10, -5],[5, 10], [511, 511])

drawLowerExtremalDependenceFunction()¶

Draw the lower extremal dependence function.

We assume that the distribution is bivariate and that its copula is denoted by $C$ . The lower extremal dependence function $u \mapsto \bar{\chi}(u)$ is defined by:

$\bar{\chi}_L(u) = \frac{2 \log u}{\log C(u,u)} - 1, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

graphGraph: The graph of the function $u \mapsto \bar{\chi}_L(u)$ .

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> graph = copula.drawLowerExtremalDependenceFunction()

drawLowerTailDependenceFunction()¶

Draw the lower tail dependence function.

We assume that the distribution is bivariate and that its copula is denoted by $C$ . The lower tail dependence function $u \mapsto \chi_L(u)$ is defined by:

$\chi_L(u) = \frac{\log (1 - C(u,u))}{\log (1-u)}, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

graphGraph: Graph of the function $u \mapsto \chi_L(u)$ .

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> graph = copula.drawLowerTailDependenceFunction()

drawMarginal1DCDF(marginalIndex, xMin, xMax, pointNumber, logScale=False)¶

Draw the cumulative distribution function of a margin.

Parameters:

iint, $1 \leq i \leq d$: The index of the margin of interest.
xMinfloat: The starting value that is used for meshing the x-axis.
xMaxfloat, xMax > xMin: The ending value that is used for meshing the x-axis.
nPointsint: The number of points that is used for meshing the x-axis.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.

Returns:

graphGraph: A graphical representation of the CDF of the requested margin.

See also

openturns.Distribution.computeCDF
openturns.Distribution.getMarginal
openturns.viewer.View
openturns.ResourceMap

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal1DCDF(2, -6.0, 6.0, 100)
>>> view = View(graph)
>>> view.show()

drawMarginal1DLogPDF(marginalIndex, xMin, xMax, pointNumber, logScale=False)¶

Draw the log-probability density function of a margin.

Parameters:

iint, $1 \leq i \leq d$: The index of the margin of interest.
xMinfloat: The starting value that is used for meshing the x-axis.
xMaxfloat, xMax > xMin: The ending value that is used for meshing the x-axis.
nPointsint: The number of points that is used for meshing the x-axis.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.

Returns:

graphGraph: A graphical representation of the log-PDF of the requested margin.

See also

openturns.Distribution.computeLogPDF
openturns.Distribution.getMarginal

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal1DLogPDF(2, -6.0, 6.0, 100)
>>> view = View(graph)
>>> view.show()

drawMarginal1DPDF(marginalIndex, xMin, xMax, pointNumber, logScale=False)¶

Draw the probability density function of a margin.

Parameters:

iint, $1 \leq i \leq d$: The index of the margin of interest.
xMinfloat: The starting value that is used for meshing the x-axis.
xMaxfloat, xMax > xMin: The ending value that is used for meshing the x-axis.
nPointsint: The number of points that is used for meshing the x-axis.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.

Returns:

graphGraph: A graphical representation of the PDF of the requested margin.

See also

openturns.Distribution.computePDF
openturns.Distribution.getMarginal

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal1DPDF(2, -6.0, 6.0, 100)
>>> view = View(graph)
>>> view.show()

drawMarginal1DSurvivalFunction(marginalIndex, xMin, xMax, pointNumber, logScale=False)¶

Draw the cumulative distribution function of a margin.

Parameters:

iint, $0 \leq i < d$: The index of the margin of interest.
xMinfloat: The starting value that is used for meshing the x-axis.
xMaxfloat, xMax > xMin: The ending value that is used for meshing the x-axis.
nPointsint: The number of points that is used for meshing the x-axis.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.

Returns:

graphGraph: A graphical representation of the SurvivalFunction of the requested margin.

See also

openturns.Distribution.computeSurvivalFunction
openturns.Distribution.getMarginal
openturns.viewer.View
openturns.ResourceMap

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal1DSurvivalFunction(2, -6.0, 6.0, 100)
>>> view = View(graph)
>>> view.show()

drawMarginal2DCDF(firstMarginal, secondMarginal, xMin, xMax, pointNumber, logScaleX=False, logScaleY=False)¶

Draw the cumulative distribution function of a couple of margins.

Parameters:

iint, $1 \leq i \leq d$: The index of the first margin of interest.
jint, $1 \leq i \neq j \leq d$: The index of the second margin of interest.
xMinlist of 2 floats: The starting values that are used for meshing the x- and y- axes.
xMaxlist of 2 floats, xMax > xMin: The ending values that are used for meshing the x- and y- axes.
nPointslist of 2 ints: The number of points that are used for meshing the x- and y- axes.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the marginal CDF of the requested couple of margins.

See also

openturns.Distribution.computeCDF
openturns.Distribution.getMarginal

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal2DCDF(2, 3, [-6.0] * 2, [6.0] * 2, [100] * 2)
>>> view = View(graph)
>>> view.show()

drawMarginal2DLogPDF(firstMarginal, secondMarginal, xMin, xMax, pointNumber, logScaleX=False, logScaleY=False)¶

Draw the log-probability density function of a couple of margins.

Parameters:

iint, $1 \leq i \leq d$: The index of the first margin of interest.
jint, $1 \leq i \neq j \leq d$: The index of the second margin of interest.
xMinlist of 2 floats: The starting values that are used for meshing the x- and y- axes.
xMaxlist of 2 floats, xMax > xMin: The ending values that are used for meshing the x- and y- axes.
nPointslist of 2 ints: The number of points that are used for meshing the x- and y- axes.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the marginal log-PDF of the requested couple of margins.

See also

openturns.Distribution.computeLogPDF
openturns.Distribution.getMarginal

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal2DLogPDF(2, 3, [-6.0] * 2, [6.0] * 2, [100] * 2)
>>> view = View(graph)
>>> view.show()

drawMarginal2DPDF(firstMarginal, secondMarginal, xMin, xMax, pointNumber, logScaleX=False, logScaleY=False)¶

Draw the probability density function of a couple of margins.

Parameters:

iint, $1 \leq i \leq d$: The index of the first margin of interest.
jint, $1 \leq i \neq j \leq d$: The index of the second margin of interest.
xMinlist of 2 floats: The starting values that are used for meshing the x- and y- axes.
xMaxlist of 2 floats, xMax > xMin: The ending values that are used for meshing the x- and y- axes.
nPointslist of 2 ints: The number of points that are used for meshing the x- and y- axes.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the marginal PDF of the requested couple of margins.

See also

openturns.Distribution.computePDF
openturns.Distribution.getMarginal

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal2DPDF(2, 3, [-6.0] * 2, [6.0] * 2, [100] * 2)
>>> view = View(graph)
>>> view.show()

drawMarginal2DSurvivalFunction(firstMarginal, secondMarginal, xMin, xMax, pointNumber, logScaleX=False, logScaleY=False)¶

Draw the cumulative distribution function of a couple of margins.

Parameters:

iint, $0 \leq i < d$: The index of the first margin of interest.
jint, $0 \leq i \neq j < d$: The index of the second margin of interest.
xMinlist of 2 floats: The starting values that are used for meshing the x- and y- axes.
xMaxlist of 2 floats, xMax > xMin: The ending values that are used for meshing the x- and y- axes.
nPointslist of 2 ints: The number of points that are used for meshing the x- and y- axes.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the marginal SurvivalFunction of the requested couple of margins.

See also

openturns.Distribution.computeSurvivalFunction
openturns.Distribution.getMarginal

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal(10)
>>> graph = distribution.drawMarginal2DSurvivalFunction(2, 3, [-6.0] * 2, [6.0] * 2, [100] * 2)
>>> view = View(graph)
>>> view.show()

drawPDF(*args)¶

Draw the graph or of iso-lines of probability density function.

Available constructors:

drawPDF(x_min, x_max, pointNumber, logScale)

drawPDF(lowerCorner, upperCorner, pointNbrInd, logScaleX, logScaleY)

drawPDF(lowerCorner, upperCorner)

Parameters:

xMinfloat, optional: The min-value of the mesh of the x-axis. Defaults uses the quantile associated to the probability level Distribution-QMin from the ResourceMap.
xMaxfloat, optional, xMax > xMin: The max-value of the mesh of the y-axis. Defaults uses the quantile associated to the probability level Distribution-QMax from the ResourceMap.
pointNumberint: The number of points that is used for meshing each axis. Defaults uses DistributionImplementation-DefaultPointNumber from the ResourceMap.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.
lowerCornersequence of float, of dimension 2, optional: The lower corner $[x_{min}, y_{min}]$ .
upperCornersequence of float, of dimension 2, optional: The upper corner $[x_{max}, y_{max}]$ .
pointNbrIndIndices, of dimension 2: Number of points that is used for meshing each axis.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the PDF or its iso_lines.

See also

openturns.Distribution.computePDF

Notes

Only valid for univariate and bivariate distributions.

Examples

View the PDF of a univariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal()
>>> graph = dist.drawPDF()
>>> graph.setLegends(['normal pdf'])

View the iso-lines PDF of a bivariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal(2)
>>> graph2 = dist.drawPDF()
>>> graph2.setLegends(['iso- normal pdf'])
>>> graph3 = dist.drawPDF([-10, -5],[5, 10], [511, 511])

drawQuantile(*args)¶

Draw the quantile function.

Parameters:

qminfloat, in $[0,1]$: The min value of the mesh of the x-axis.
qmaxfloat, in $[0,1]$: The max value of the mesh of the x-axis.
nPointsint, optional: The number of points that is used for meshing the quantile curve. Defaults uses DistributionImplementation-DefaultPointNumber from the ResourceMap.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.

Returns:

graphGraph: A graphical representation of the quantile function.

See also

openturns.Distribution.computeQuantile
openturns.viewer.View
openturns.ResourceMap

Notes

This is implemented for univariate and bivariate distributions only. In the case of bivariate distributions, defined by its CDF $F$ and its marginals $(F_1, F_2)$ , the quantile of order $q$ is the point $(F_1(u),F_2(u))$ defined by

F(F_1(u), F_2(u)) = q

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> distribution = ot.Normal()
>>> graph = distribution.drawQuantile()
>>> view = View(graph)
>>> view.show()
>>> distribution = ot.JointDistribution([ot.Normal(), ot.Exponential(1.0)], ot.ClaytonCopula(0.5))
>>> graph = distribution.drawQuantile()
>>> view = View(graph)
>>> view.show()

drawSurvivalFunction(*args)¶

Draw the cumulative distribution function.

Available constructors:

drawSurvivalFunction(x_min, x_max, pointNumber, logScale)

drawSurvivalFunction(lowerCorner, upperCorner, pointNbrInd, logScaleX, logScaleY)

drawSurvivalFunction(lowerCorner, upperCorner)

Parameters:

xMinfloat, optional: The min-value of the mesh of the x-axis. Defaults uses the quantile associated to the probability level Distribution-QMin from the ResourceMap.
xMaxfloat, optional, xMax > xMin: The max-value of the mesh of the y-axis. Defaults uses the quantile associated to the probability level Distribution-QMax from the ResourceMap.
pointNumberint: The number of points that is used for meshing each axis. Defaults uses DistributionImplementation-DefaultPointNumber from the ResourceMap.
logScalebool: Flag to tell if the plot is done on a logarithmic scale. Default is False.
lowerCornersequence of float, of dimension 2, optional: The lower corner $[x_{min}, y_{min}]$ .
upperCornersequence of float, of dimension 2, optional: The upper corner $[x_{max}, y_{max}]$ .
pointNbrIndIndices, of dimension 2: Number of points that is used for meshing each axis.
logScaleXbool: Flag to tell if the plot is done on a logarithmic scale for X. Default is False.
logScaleYbool: Flag to tell if the plot is done on a logarithmic scale for Y. Default is False.

Returns:

graphGraph: A graphical representation of the SurvivalFunction.

See also

openturns.Distribution.computeSurvivalFunction

Notes

Only valid for univariate and bivariate distributions.

Examples

View the SurvivalFunction of a univariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal()
>>> graph = dist.drawSurvivalFunction()
>>> graph.setLegends(['normal cdf'])

View the iso-lines SurvivalFunction of a bivariate distribution:

>>> import openturns as ot
>>> dist = ot.Normal(2)
>>> graph2 = dist.drawSurvivalFunction()
>>> graph2.setLegends(['iso- normal cdf'])
>>> graph3 = dist.drawSurvivalFunction([-10, -5],[5, 10], [511, 511])

drawUpperExtremalDependenceFunction()¶

Draw the upper extremal dependence function.

We assume that the distribution is bivariate and that its copula is denoted by $C$ . The upper extremal dependence function $u \mapsto \bar{\chi}(u)$ is defined by:

$\bar{\chi}(u) = \frac{2 \log 1-u}{\log \bar{C}(u,u)} - 1, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

graphGraph: Graph of the function $u \mapsto \bar{\chi}(u)$ .

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> graph = copula.drawUpperExtremalDependenceFunction()

drawUpperTailDependenceFunction()¶

Draw the upper tail dependence function.

We assume that the distribution is bivariate and that its copula is denoted by $C$ . The upper tail dependence function $u \mapsto \chi(u)$ is defined by:

$\chi(u) = 2 - \frac{\log C(u,u)}{\log u}, \forall u \in [0,1]$

Refer to Tail dependence coefficients to get more details.

Returns:

graphGraph: Graph of the function $u \mapsto \chi(u)$ .

Examples

>>> import openturns as ot
>>> copula = ot.FrankCopula()
>>> graph = copula.drawUpperTailDependenceFunction()

exp()¶

Transform distribution by exponential function.

Returns:

distDistribution: The transformed distribution.

getCDFEpsilon()¶

Accessor to the CDF computation precision.

Returns:

CDFEpsilonfloat: CDF computation precision.

getCentralMoment(n)¶

Accessor to the componentwise central moments.

Parameters:

kint: The order of the central moment.

Returns:

mPoint: Componentwise central moment of order k.

See also

getMoment

Notes

Central moments are centered with respect to the first-order moment:

$\vect{m}^{(k)}_0 = \Tr{\left(\Expect{\left(X_i - \mu_i\right)^k}, \quad i = 1, \ldots, n\right)}$

getCholesky()¶

Accessor to the Cholesky factor of the covariance matrix.

Returns:

LTriangularMatrix: Cholesky factor of the covariance matrix.

See also

getCovariance

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getCopula()¶

Accessor to the copula of the distribution.

Returns:

CDistribution: Copula of the distribution.

See also

openturns.JointDistribution

getCorrelation()¶

Accessor to the correlation matrix.

Returns:

RCorrelationMatrix: The correlation matrix of the distribution.

Notes

$R_{ij} = \dfrac{C_{ij}}{\sigma_i\sigma_j}$

where the $(\sigma_i)$ are the margin standard deviations and $(C_{ij})$ the covariance coefficients.

getCovariance()¶

Accessor to the covariance matrix.

Returns:

SigmaCovarianceMatrix: Covariance matrix.

Notes

The covariance is the second-order central moment. It is defined as:

$\mat{\Sigma} & = \Cov{\vect{X}} \\ & = \Expect{\left(\vect{X} - \vect{\mu}\right) \Tr{\left(\vect{X} - \vect{\mu}\right)}}$

getDescription()¶

Accessor to the componentwise description.

Returns:

descriptionDescription: Description of the components of the distribution.

See also

setDescription

getDimension()¶

Accessor to the dimension of the distribution.

Returns:

nint: The number of components in the distribution.

getDispersionIndicator()¶

Dispersion indicator accessor.

Defines a generic metric of the dispersion. When the standard deviation is not defined it falls back to the interquartile. Only available for 1-d distributions.

Returns:

dispersionfloat: Standard deviation or interquartile.

getIntegrationNodesNumber()¶

Accessor to the number of Gauss integration points.

Returns:

Nint: Number of integration points.

getInverseCholesky()¶

Accessor to the inverse Cholesky factor of the covariance matrix.

Returns:

LinvTriangularMatrix: Inverse Cholesky factor of the covariance matrix.

See also

openturns.Distribution.getCholesky

getInverseIsoProbabilisticTransformation()¶

Accessor to the inverse iso-probabilistic transformation.

Returns:

TinvFunction: Inverse iso-probabilistic transformation.

See also

openturns.Distribution.getIsoProbabilisticTransformation

Notes

The inverse iso-probabilistic transformation is defined as follows:

$T^{-1}: \left|\begin{array}{rcl} \Rset^n & \rightarrow & \supp{\vect{X}} \\ \vect{u} & \mapsto & \vect{x} \end{array}\right.$

getIsoProbabilisticTransformation()¶

Accessor to the iso-probabilistic transformation.

Refer to Isoprobabilistic transformations.

Returns:

TFunction: Iso-probabilistic transformation.

See also

openturns.Distribution.getInverseIsoProbabilisticTransformation
openturns.Distribution.isElliptical
openturns.Distribution.hasEllipticalCopula

Notes

The iso-probabilistic transformation is defined as follows:

$T: \left|\begin{array}{rcl} \supp{\vect{X}} & \rightarrow & \Rset^n \\ \vect{x} & \mapsto & \vect{u} \end{array}\right.$

An iso-probabilistic transformation is a diffeomorphism [1] from $\supp{\vect{X}}$ to $\Rset^d$ that maps realizations $\vect{x}$ of a random vector $\vect{X}$ into realizations $\vect{y}$ of another random vector $\vect{Y}$ while preserving probabilities. It is hence defined so that it satisfies:

$\begin{eqnarray*} \Prob{\bigcap_{i=1}^d X_i \leq x_i} & = & \Prob{\bigcap_{i=1}^d Y_i \leq y_i} \\ F_{\vect{X}}(\vect{x}) & = & F_{\vect{Y}}(\vect{y}) \end{eqnarray*}$

The present implementation of the iso-probabilistic transformation maps realizations $\vect{x}$ into realizations $\vect{u}$ of a random vector $\vect{U}$ with spherical distribution [2]. To be more specific:

if the distribution is elliptical, then the transformed distribution is simply made spherical using the Nataf (linear) transformation.

if the distribution has an elliptical Copula, then the transformed distribution is made spherical using the generalized Nataf transformation.

otherwise, the transformed distribution is the standard multivariate Normal distribution and is obtained by means of the Rosenblatt transformation.

getKendallTau()¶

Accessor to the Kendall coefficients matrix.

Returns:

tauCorrelationMatrix: Kendall coefficients matrix.

See also

getSpearmanCorrelation

Notes

The Kendall coefficients matrix is defined as:

$\mat{\tau} = \Big[& \Prob{X_i < x_i \cap X_j < x_j \cup X_i > x_i \cap X_j > x_j} \\ & - \Prob{X_i < x_i \cap X_j > x_j \cup X_i > x_i \cap X_j < x_j}, \quad i,j = 1, \ldots, n\Big]$

getKurtosis()¶

Accessor to the componentwise kurtosis.

Returns:

kPoint: Componentwise kurtosis.

Notes

The kurtosis is the fourth-order central moment standardized by the standard deviation:

$\vect{\kappa} = \Tr{\left(\Expect{\left(\frac{X_i - \mu_i} {\sigma_i}\right)^4}, \quad i = 1, \ldots, n\right)}$

getMarginal(*args)¶

Accessor to marginal distributions.

Parameters:

iint or list of ints, $0 \leq i < d$: Component(s) indice(s).

Returns:

distributionDistribution: The marginal distribution of the selected component(s).

getMean()¶

Accessor to the mean.

Returns:

kPoint: Mean.

Notes

The mean is the first-order moment:

$\vect{\mu} = \Tr{\left(\Expect{X_i}, \quad i = 1, \ldots, n\right)}$

getMoment(n)¶

Accessor to the componentwise moments.

Parameters:

kint: The order of the moment.

Returns:

mPoint: Componentwise moment of order k.

Notes

The componentwise moment of order $k$ is defined as:

$\vect{m}^{(k)} = \Tr{\left(\Expect{X_i^k}, \quad i = 1, \ldots, d\right)}$

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getPDFEpsilon()¶

Accessor to the PDF computation precision.

Returns:

PDFEpsilonfloat: PDF computation precision.

getParameter()¶

Accessor to the parameter of the distribution.

Returns:

parameterPoint: Parameter values.

getParameterDescription()¶

Accessor to the parameter description of the distribution.

Returns:

descriptionDescription: Parameter names.

getParameterDimension()¶

Accessor to the number of parameters in the distribution.

Returns:

n_parametersint: Number of parameters in the distribution.

See also

getParametersCollection

getParametersCollection()¶

Accessor to the parameter of the distribution.

Returns:

parametersPointWithDescription: Dictionary-like object with parameters names and values.

getPearsonCorrelation()¶

Accessor to the Pearson correlation matrix.

Returns:

RCorrelationMatrix: Pearson’s correlation matrix.

See also

getCovariance

Notes

Pearson’s correlation is defined as the normalized covariance matrix:

$\mat{\rho} & = \left[\frac{\Cov{X_i, X_j}}{\sqrt{\Var{X_i}\Var{X_j}}}, \quad i,j = 1, \ldots, d\right] \\ & = \left[\frac{\Sigma_{i,j}}{\sqrt{\Sigma_{i,i}\Sigma_{j,j}}}, \quad i,j = 1, \ldots, d\right]$

getPositionIndicator()¶

Position indicator accessor.

Defines a generic metric of the position. When the mean is not defined it falls back to the median. Available only for 1-d distributions.

Returns:

positionfloat: Mean or median of the distribution.

getProbabilities()¶

Accessor to the discrete probability levels.

Returns:

probabilitiesPoint: The probability levels of a discrete distribution.

getRange()¶

Accessor to the range of the distribution.

Returns:

rangeInterval: Range of the distribution.

See also

getSupport

Notes

The mathematical range is the smallest closed interval outside of which the PDF is zero. The numerical range is the interval outside of which the PDF is rounded to zero in double precision.

getRealization()¶

Accessor to a pseudo-random realization from the distribution.

Refer to Distribution realizations.

Returns:

pointPoint: A pseudo-random realization of the distribution.

See also

getSample, getSampleByInversion, getSampleByQMC

getRoughness()¶

Accessor to roughness of the distribution.

Returns:

rfloat: Roughness of the distribution.

See also

computePDF

Notes

The roughness of the distribution is defined as the $\cL^2$ -norm of its PDF:

$r = \int_{\supp{\vect{X}}} f_{\vect{X}}(\vect{x})^2 \di{\vect{x}}$

getSample(size)¶

Accessor to a pseudo-random sample from the distribution.

Parameters:

sizeint: Sample size.

Returns:

sampleSample: A pseudo-random sample of the distribution.

See also

getRealization, getSampleByInversion, getSampleByQMC

getSampleByInversion(size)¶

Accessor to a pseudo-random sample from the distribution.

Parameters:

sizeint: Sample size.

Returns:

sampleSample: A pseudo-random sample of the distribution based on conditional quantiles.

See also

openturns.Distribution.getRealization
openturns.RandomGenerator
openturns.Distribution.getSample
openturns.Distribution.getSampleByQMC

getSampleByQMC(size)¶

Accessor to a low discrepancy sample from the distribution.

Parameters:

sizeint: Sample size.

Returns:

sampleSample: A low discrepancy sample of the distribution based on Sobol’s sequences and conditional quantiles.

See also

openturns.Distribution.getRealization
openturns.RandomGenerator
openturns.Distribution.getSample
openturns.Distribution.getSampleByInversion

getShapeMatrix()¶

Accessor to the shape matrix of the underlying copula if it is elliptical.

Returns:

shapeCorrelationMatrix: Shape matrix of the elliptical copula of a distribution.

See also

getPearsonCorrelation

Notes

This is not the Pearson correlation matrix.

getShiftedMoment(n, shift)¶

Accessor to the componentwise shifted moments.

Parameters:

kint: The order of the shifted moment.
shiftsequence of float: The shift of the moment.

Returns:

mPoint: Componentwise central moment of order k.

See also

getMoment, getCentralMoment

Notes

The moments are centered with respect to the given shift $\vect{s}$ :

$\vect{m}^{(k)}_0 = \Tr{\left(\Expect{\left(X_i - s_i\right)^k}, \quad i = 1, \ldots, n\right)}$

getSingularities()¶

Accessor to the singularities of the PDF function.

It is defined for univariate distributions only, and gives all the singularities (i.e. discontinuities of any order) strictly inside of the range of the distribution.

Returns:

singularitiesPoint: The singularities of the PDF of an univariate distribution.

getSkewness()¶

Accessor to the componentwise skewness.

Returns:

dPoint: Componentwise skewness.

Notes

The skewness is the third-order central moment standardized by the standard deviation:

$\vect{\delta} = \Tr{\left(\Expect{\left(\frac{X_i - \mu_i} {\sigma_i}\right)^3}, \quad i = 1, \ldots, d\right)}$

getSpearmanCorrelation()¶

Accessor to the Spearman correlation matrix.

Returns:

RCorrelationMatrix: Spearman’s correlation matrix.

See also

getKendallTau

Notes

Spearman’s (rank) correlation is defined as the normalized covariance matrix of the copula (ie that of the uniform margins):

$\mat{\rho_S} = \left[\frac{\Cov{F_{X_i}(X_i), F_{X_j}(X_j)}} {\sqrt{\Var{F_{X_i}(X_i)} \Var{F_{X_j}(X_j)}}}, \quad i,j = 1, \ldots, d\right]$

getStandardDeviation()¶

Accessor to the componentwise standard deviation.

The standard deviation is the square root of the variance.

Returns:

sigmaPoint: Componentwise standard deviation.

See also

getCovariance

getStandardDistribution()¶

Accessor to the standard distribution.

Returns:

standard_distributionDistribution: Standard distribution.

See also

getIsoProbabilisticTransformation

Notes

The standard distribution is determined according to the distribution properties. This is the target distribution achieved by the iso-probabilistic transformation.

getStandardRepresentative()¶

Accessor to the standard representative distribution in the parametric family.

Returns:

std_repr_distDistribution: Standard representative distribution.

Notes

The standard representative distribution is defined on a distribution-by-distribution basis, most of the time by scaling the distribution with bounded support to $[0,1]$ or by standardizing (ie zero mean, unit variance) the distributions with unbounded support. It is the member of the family for which orthonormal polynomials will be built using generic algorithms of orthonormalization (see StandardDistributionPolynomialFactory).

getSupport(*args)¶

Accessor to the support of the distribution.

Parameters:

intervalInterval: An interval to intersect with the support of the discrete part of the distribution.

Returns:

supportInterval: The intersection of the support of the discrete part of the distribution with the given interval.

See also

getRange

Notes

The mathematical support $\supp{\vect{X}}$ of the discrete part of a distribution is the collection of points with nonzero probability.

This is yet implemented for discrete distributions only.

hasEllipticalCopula()¶

Test whether the copula of the distribution is elliptical or not.

Returns:

testbool: Answer.

See also

isElliptical

hasIndependentCopula()¶

Test whether the copula of the distribution is the independent one.

Returns:

testbool: Answer.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

inverse()¶

Transform distribution by inverse function.

Returns:

distDistribution: The transformed distribution.

isContinuous()¶

Test whether the distribution is continuous or not.

Returns:

testbool: Answer.

isCopula()¶

Test whether the distribution is a copula or not.

Returns:

testbool: Answer.

Notes

A copula is a distribution with uniform margins on [0; 1].

isDiscrete()¶

Test whether the distribution is discrete or not.

Returns:

testbool: Answer.

isElliptical()¶

Test whether the distribution is elliptical or not.

Returns:

testbool: Answer.

Notes

A multivariate distribution is said to be elliptical if its characteristic function is of the form:

$\phi(\vect{t}) = \exp\left(i \Tr{\vect{t}} \vect{\mu}\right) \Psi\left(\Tr{\vect{t}} \mat{\Sigma} \vect{t}\right), \quad \vect{t} \in \Rset^d$

for specified vector $\vect{\mu}$ and positive-definite matrix $\mat{\Sigma}$ . The function $\Psi$ is known as the characteristic generator of the elliptical distribution.

isIntegral()¶

Test whether the distribution is integer-valued or not.

Returns:

testbool: Answer.

ln()¶

Transform distribution by natural logarithm function.

Returns:

distDistribution: The transformed distribution.

log()¶

Transform distribution by natural logarithm function.

Returns:

distDistribution: The transformed distribution.

setDescription(description)¶

Accessor to the componentwise description.

Parameters:

descriptionsequence of str: Description of the components of the distribution.

setIntegrationNodesNumber(integrationNodesNumber)¶

Accessor to the number of Gauss integration points.

Parameters:

Nint: Number of integration points.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setParameter(parameters)¶

Accessor to the parameter of the distribution.

Parameters:

parametersequence of float: Parameter values.

setParametersCollection(*args)¶

Accessor to the parameter of the distribution.

Parameters:

parametersPointWithDescription: Dictionary-like object with parameters names and values.

sin()¶

Transform distribution by sine function.

Returns:

distDistribution: The transformed distribution.

sinh()¶

Transform distribution by sinh function.

Returns:

distDistribution: The transformed distribution.

sqr()¶

Transform distribution by square function.

Returns:

distDistribution: The transformed distribution.

sqrt()¶

Transform distribution by square root function.

Returns:

distDistribution: The transformed distribution.

tan()¶

Transform distribution by tangent function.

Returns:

distDistribution: The transformed distribution.

tanh()¶

Transform distribution by tanh function.

Returns:

distDistribution: The transformed distribution.

Examples using the class¶

Estimate moments from sample

Sample manipulation

Quick start guide to distributions

Posterior sampling using a PythonDistribution

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

IndependentCopula¶

Examples using the class¶