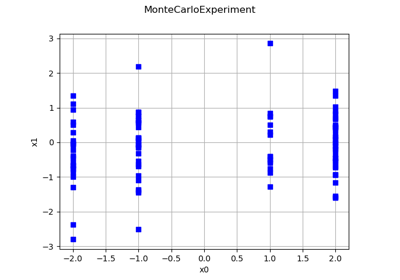
MonteCarloExperiment¶
(Source code, png)
- class MonteCarloExperiment(*args)¶
MonteCarlo experiment.
- Available constructors:
MonteCarloExperiment(distribution, size)
MonteCarloExperiment(size)
- Parameters:
- distribution
Distribution Distribution
with an independent copula used to generate the set of input data.
- sizepositive int
Number
of points that will be generated in the experiment.
- distribution
See also
Notes
MonteCarloExperiment is a random weighted design of experiments (see [hammersley1961] page 51, [lemieux2009] page 3). The
generate()method computes the nodesby generating independent observations from the distribution
. The weights associated to the points are all equal to
where
is the sample size. When the
generate()method is called a second time, the generated sample changes.Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> experiment = ot.MonteCarloExperiment(ot.Normal(2), 5) >>> print(experiment.generate()) [ X0 X1 ] 0 : [ 0.608202 -1.26617 ] 1 : [ -0.438266 1.20548 ] 2 : [ -2.18139 0.350042 ] 3 : [ -0.355007 1.43725 ] 4 : [ 0.810668 0.793156 ]
Methods
generate()Generate points according to the type of the experiment.
Generate points and their associated weight according to the type of the experiment.
Accessor to the object's name.
Accessor to the distribution.
getName()Accessor to the object's name.
getSize()Accessor to the size of the generated sample.
hasName()Test if the object is named.
Ask whether the experiment has uniform weights.
isRandom()Accessor to the randomness of quadrature.
setDistribution(distribution)Accessor to the distribution.
setName(name)Accessor to the object's name.
setSize(size)Accessor to the size of the generated sample.
- __init__(*args)¶
- generate()¶
Generate points according to the type of the experiment.
- Returns:
- sample
Sample Points
of the design of experiments. The sampling method is defined by the type of the weighted experiment.
- sample
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5) >>> sample = myExperiment.generate() >>> print(sample) [ X0 X1 ] 0 : [ 0.608202 -1.26617 ] 1 : [ -0.438266 1.20548 ] 2 : [ -2.18139 0.350042 ] 3 : [ -0.355007 1.43725 ] 4 : [ 0.810668 0.793156 ]
- generateWithWeights()¶
Generate points and their associated weight according to the type of the experiment.
- Returns:
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5) >>> sample, weights = myExperiment.generateWithWeights() >>> print(sample) [ X0 X1 ] 0 : [ 0.608202 -1.26617 ] 1 : [ -0.438266 1.20548 ] 2 : [ -2.18139 0.350042 ] 3 : [ -0.355007 1.43725 ] 4 : [ 0.810668 0.793156 ] >>> print(weights) [0.2,0.2,0.2,0.2,0.2]
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getDistribution()¶
Accessor to the distribution.
- Returns:
- distribution
Distribution Distribution of the input random vector.
- distribution
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getSize()¶
Accessor to the size of the generated sample.
- Returns:
- sizepositive int
Number
of points constituting the design of experiments.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- hasUniformWeights()¶
Ask whether the experiment has uniform weights.
- Returns:
- hasUniformWeightsbool
Whether the experiment has uniform weights.
- isRandom()¶
Accessor to the randomness of quadrature.
- Parameters:
- isRandombool
Is true if the design of experiments is random. Otherwise, the design of experiment is assumed to be deterministic.
- setDistribution(distribution)¶
Accessor to the distribution.
- Parameters:
- distribution
Distribution Distribution of the input random vector.
- distribution
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setSize(size)¶
Accessor to the size of the generated sample.
- Parameters:
- sizepositive int
Number
of points constituting the design of experiments.
Examples using the class¶
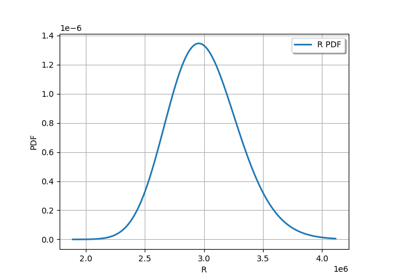
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
Axial stressed beam : comparing different methods to estimate a probability
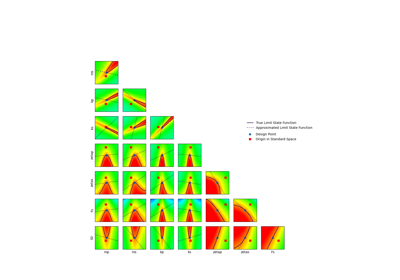
Using the FORM - SORM algorithms on a nonlinear function
Create a design of experiments with discrete and continuous variables
 OpenTURNS
OpenTURNS