IshigamiModel¶
- class IshigamiModel¶
Data class for the Ishigami model.
Examples
>>> from openturns.usecases import ishigami_function >>> # Load the Ishigami model >>> im = ishigami_function.IshigamiModel()
- Attributes:
- dimThe dimension of the problem
dim = 3
- aConstant
a = 7.0
- bConstant
b = 0.1
- X1Uniform distribution
First marginal, ot.Uniform(-np.pi, np.pi)
- X2Uniform distribution
Second marginal, ot.Uniform(-np.pi, np.pi)
- X3Uniform distribution
Third marginal, ot.Uniform(-np.pi, np.pi)
- distributionXJointDistribution
The joint distribution of the input parameters.
- ishigamiSymbolicFunction
The Ishigami model with a, b as variables.
- modelParametricFunction
The Ishigami model with the a=7.0 and b=0.1 parameters fixed.
- expectationConstant
Expectation of the output variable.
- varianceConstant
Variance of the output variable.
- S1Constant
First order Sobol index number 1
- S2Constant
First order Sobol index number 2
- S3Constant
First order Sobol index number 3
- S12Constant
Second order Sobol index for marginals 1 and 2.
- S13Constant
Second order Sobol index for marginals 1 and 3.
- S23Constant
Second order Sobol index for marginals 2 and 3.
- S123Constant
- ST1Constant
Total order Sobol index number 1.
- ST2Constant
Total order Sobol index number 2.
- ST3Constant
Total order Sobol index number 3.
- __init__()¶
Examples using the class¶
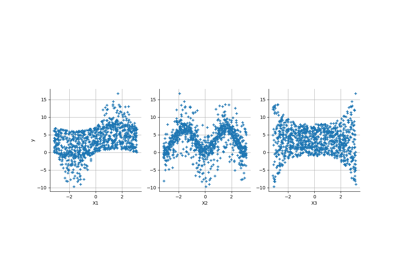
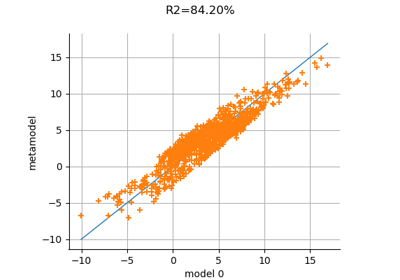
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
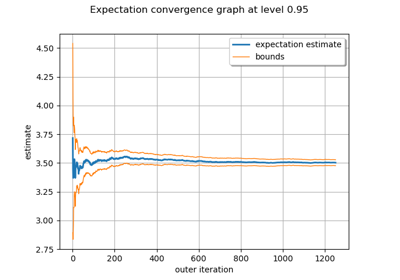
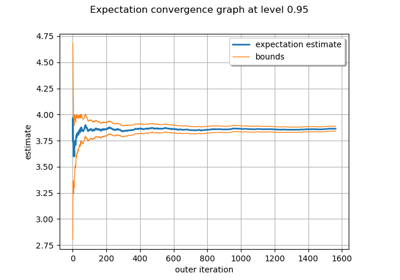
Evaluate the mean of a random vector by simulations
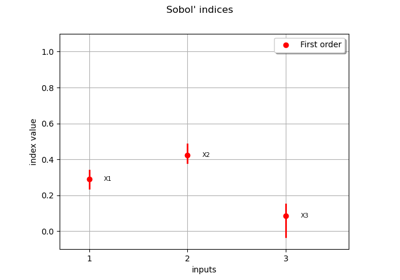
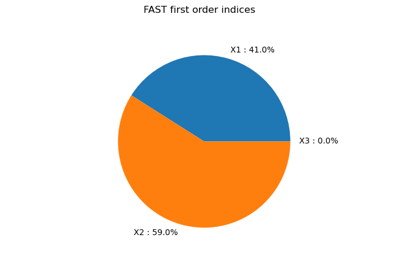
Sobol’ sensitivity indices using rank-based algorithm
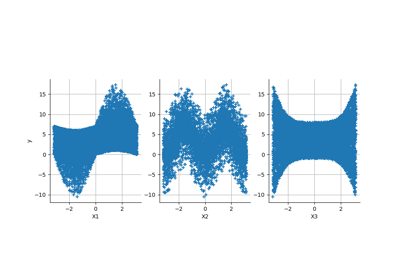
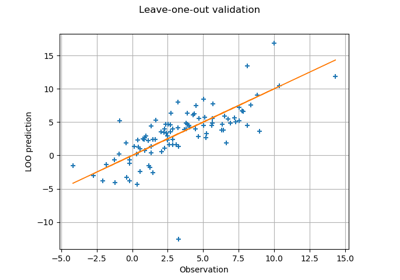
Compute leave-one-out error of a polynomial chaos expansion
 OpenTURNS
OpenTURNS