Note

Go to the end to download the full example code.

Create a sparse chaos by integration¶

The goal of this example is to show how to create a sparse polynomial chaos expansion (PCE) when we estimate its coefficients by integration. We show how to use the CleaningStrategy class.

Polynomial chaos expansion¶

Let $g : \mathcal{D} \rightarrow \mathbb{R}$ be a function where $\mathcal{D} \subseteq \mathbb{R}^p$ is the domain of $g$ . We consider $\vect{X}$ a random vector which probability density function is denoted by $f$ . We assume that $g(\vect{X})$ has a finite second order moment. Let $T$ be an iso-probabilistic transformation such that $\vect{Z} = T(\vect{X})$ follows a distribution uniquely defined by all its moments. Let $h$ be the function defined by:

$h = g \circ T^{-1}.$

The polynomial chaos decomposition of $h$ with respect to the measure of $\vect{Z}$ is (see [blatman2009] page 73) :

$h(\vect{z}) = \sum_{\vect{\alpha} \in \mathbb{N}^p} a_{\vect{\alpha}} \psi_{\vect{\alpha}}(\vect{z})$

where $\vect{\alpha} = (\alpha_1, ..., \alpha_p) \in \mathbb{N}^p$ is a multi-index, $a_{\vect{\alpha}} \in \mathbb{R}$ is the coefficient, $\psi_{\vect{\alpha}} : \mathcal{\bar{X}} \rightarrow \mathbb{R}$ is a multivariate polynomial.

Truncated expansion¶

In practice, we cannot consider an infinite series and must truncate the decomposition at a given order. Only a selection of coefficients must be kept. This leads to a subset of all possible multi-indices. In the remainder of this text, we call this selection the multi-index set.

Several multi-index sets can be considered. A simple method is to truncate the polynomial up to a given maximum total degree $d \in \mathbb{N}$ . Let $\mathcal{A}^{d}$ be the multi-index set defined by

$\mathcal{A}^{d} = \left\{ \vect{\alpha} \in \mathbb{N}^p \; | \; \|\vect{\alpha}\|_1 \leq d\right\}$

where

$\|\vect{\alpha}\|_d = \alpha_1 + ... + \alpha_p$

is the 1-norm of the multi-index $\vect{\alpha}$ . Therefore, the truncated polynomial chaos expansion is:

$\widetilde{h}(\vect{z}) = \sum_{\vect{\alpha} \in \mathcal{A}^{d}} a_{\vect{\alpha}} \psi_{\vect{\alpha}}(\vect{z}).$

In order to ensure a low error, we may choose a large value of the parameter $P$ . This, however, leads to a large number of coefficients $\vect{\alpha} \in \mathcal{A}^{d}$ to estimate. More precisely, the number of coefficients to estimate is (see [blatman2009] page 73) :

$\textrm{card}\left(\mathcal{A}^{d}\right) = {p + d \choose d} = \frac{(p + d)!}{p! d!}$

where $p!$ is the factorial number of $p$ .

Low-rank polynomial chaos expansion¶

For any $\vect{\alpha} \in \mathbb{N}^p$ , let $\|\vect{\alpha}\|_0$ be the rank of the multi-index, that is, the number of non-zero components:

$\|\vect{\alpha}\|_0 = \sum_{i = 1}^p \vect{1}_{\alpha_i > 0}$

where $\vect{1}$ is the indicator function. The multi-index set of maximum total degree $d \in \mathbb{N}$ and maximum rank $j \in \mathbb{N}$ is ([blatman2009] page 74):

$\mathcal{A}^{d,j} = \left\{ \vect{\alpha} \in \mathbb{N}^p \; | \; \|\vect{\alpha}\|_1 \leq d, \; \; \|\vect{\alpha}\|_0 \leq j\right\}.$

Therefore, the rank-j polynomial chaos expansion is:

$\widetilde{h}(\vect{z}) = \sum_{\vect{\alpha} \in \mathcal{A}^{d,j}} a_{\vect{\alpha}} \psi_{\vect{\alpha}}(\vect{z}).$

The rank is now a hyperparameter of the model: [blatman2009] suggests to use $j = 2, 3, 4$ . An example of low-rank PCE for the G-Sobol’ function is given in [blatman2009] page 75.

Note. It is currently not possible to create a low-rank PCE.

Model selection¶

If $\textrm{Card}\left(\mathcal{A}^{d}\right)$ is large, many coefficients may be poorly estimated, which may reduce the quality of the metamodel. We may want to select a subset of the coefficients which best predict the output. In other words, we may compute a subset:

$\mathcal{A} \subseteq \mathcal{A}^{d}$

such that ([blatman2009] page 86) :

$\widetilde{h}(\vect{z}) = \sum_{\vect{\alpha} \in \mathcal{A}} a_{\vect{\alpha}} \psi_{\vect{\alpha}}(\vect{z})$

An enumeration rule is a function from the set of integers $k$ to the corresponding set of multi-indices $\vect{\alpha}$ . More precisely, let $r : \mathbb{N} \rightarrow \mathbb{N}^p$ be the function such that :

$r(k) = \vect{\alpha}$

for any $k \geq 0$ . Let $K \in \mathbb{N}$ be a parameter representing the number of coefficients considered in the selection. Given an enumeration rule for the multi-indices $\vect{\alpha}$ , at most $K$ multi-indices will be considered. Let $\mathcal{A}_K$ be the corresponding multi-index set :

$\mathcal{A}_K = \left\{ \vect{\alpha} \; | \; r^{-1}(\vect{\alpha}) = k \leq K \right\}.$

Let $\epsilon > 0$ be a parameter representing the minimum relative value of a significant coefficient $a_{\vect{\alpha}}$ . The CleaningStrategy uses the following criterion to select the coefficients :

$\mathcal{A}_\epsilon = \left\{ |a_{\vect{\alpha}}| \geq \epsilon \max_{ a_{\vect{\alpha}} \in \mathcal{A}_K } |a_{\vect{\alpha}}| \right\}$

where $\epsilon$ is the significance factor, which by default is $\epsilon = 10^{-4}$ . This rule selects only the coefficients which are significantly different from zero.

Sparsity index¶

The sparsity index of a multi-index set is the ratio of the cardinality of the multi-index set to the cardinality of the multi-index set of the equivalent multi-index with maximum total degree. For a given multi-index set $\mathcal{A}$ , let $d$ be the maximum 1-norm of multi-indices in the set :

$d := \textrm{max}_{\vect{\alpha} \in \mathcal{A}} \|\vect{\alpha}\|_1.$

The index of sparsity of $\mathcal{A}$ is ([blatman2009] eq. 4.42 page 86) :

$\textrm{IS}(\mathcal{A}) = \frac{\textrm{card}(\mathcal{A})}{\textrm{card}\left(\mathcal{A}^d\right)}.$

Note. The index of sparsity as defined by [blatman2009] is close to zero when the model is very sparse. The following complementary indicator is close to 1 when the model is very sparse:

$\textrm{IS}_{\textrm{c}}(\mathcal{A}) = 1 - \frac{\textrm{card}(\mathcal{A})}{\textrm{card}\left(\mathcal{A}^d\right)}.$

import openturns as ot
import openturns.viewer as otv
from openturns.usecases import ishigami_function
import itertools

The following function takes a polynomial chaos result as input and prints a given maximum number of coefficients of this polynomial. It can take into account a threshold, so that we can avoid to print coefficients which are very close to zero.

def printCoefficientsTable(
    polynomialChaosResult, maximum_number_of_printed_coefficients=10, threshold=0.0
):
    """
    Print the coefficients of the polynomial chaos.

    Parameters
    ----------
    polynomialChaosResult : ot.FunctionalChaosResult
        The polynomial chaos expansion.
    maximum_number_of_printed_coefficients : int
        The maximum number of printed coefficients.
    threshold : float, strictly positive
        If a coefficient has an absolute value strictly greater than the
        threshold, it is printed.
    """
    basis = polynomialChaosResult.getOrthogonalBasis()
    coefficients = polynomialChaosResult.getCoefficients()
    enumerate_function = basis.getEnumerateFunction()
    indices = polynomialChaosResult.getIndices()
    nbcoeffs = indices.getSize()
    print("Total number of coefficients : ", nbcoeffs)
    print("# Indice, Multi-indice, Degree : Value")
    print_index = 0
    for k in range(nbcoeffs):
        multiindex = enumerate_function(indices[k])
        degree = sum(multiindex)
        c = coefficients[k][0]
        if abs(c) > threshold:
            print("#%d, %s (%s) : %s" % (k, multiindex, degree, c))
            print_index += 1
        if print_index > maximum_number_of_printed_coefficients:
            break
    return

The next function computes the polynomial chaos $R^2$ score using simple validation on a test sample generated by Monte-Carlo sampling. The actual computation is performed by the MetaModelValidation class.

def compute_polynomial_chaos_R2(
    polynomialchaos_result, g_function, input_distribution, n_valid=1000
):
    """
    Compute the R2 score of the polynomial chaos.


    Parameters
    ----------
    polynomialChaosResult : ot.FunctionalChaosResult
        The polynomial chaos expansion.
    g_function : ot.Function
        The function.
    input_distribution : ot.Distribution
        The input distribution.
    n_valid : int
        The number of simulations to compute the R2 score.

    Returns
    -------
    r2Score : float
        The R2 score
    """
    ot.RandomGenerator.SetSeed(1976)
    metamodel = polynomialchaos_result.getMetaModel()
    inputTest = input_distribution.getSample(n_valid)
    outputTest = g_function(inputTest)
    metamodelPredictions = metamodel(inputTest)
    val = ot.MetaModelValidation(outputTest, metamodelPredictions)
    r2Score = val.computeR2Score()[0]
    return r2Score

The following function creates a validation plot using the drawValidation() method of the MetaModelValidation class.

def draw_polynomial_chaos_validation(
    polynomialchaos_result, g_function, input_distribution, n_valid=1000
):
    """
    Validate the polynomial chaos.

    Create the validation plot.


    Parameters
    ----------
    polynomialChaosResult : ot.FunctionalChaosResult
        The polynomial chaos expansion.
    g_function : ot.Function
        The function.
    input_distribution : ot.Distribution
        The input distribution.
    n_valid : int
        The number of simulations to compute the R2 score.

    Returns
    -------
    view : ot.View
        The plot.
    """
    metamodel = polynomialchaos_result.getMetaModel()
    inputTest = input_distribution.getSample(n_valid)
    outputTest = g_function(inputTest)
    metamodelPredictions = metamodel(inputTest)
    val = ot.MetaModelValidation(outputTest, metamodelPredictions)
    r2Score = val.computeR2Score()[0]
    graph = val.drawValidation()
    graph.setTitle("R2=%.2f%%" % (r2Score * 100))
    view = otv.View(graph, figure_kw={"figsize": (5.0, 4.0)})
    return view

We consider the Ishigami model. Its three inputs are i.i.d. random variables that follow the uniform distribution on the $[-\pi, \pi]$ interval. This is an interesting example for our purpose because it is highly non-linear, so that a high polynomial degree will be required in order to produce a polynomial chaos expansion with $R^2$ score sufficiently close to 1.

im = ishigami_function.IshigamiModel()

im.inputDistribution.setDescription(["`X_0`", "`X_1`", "`X_2`"])
im.model.setOutputDescription(["`Y`"])
print(im.inputDistribution)

JointDistribution(Uniform(a = -3.14159, b = 3.14159), Uniform(a = -3.14159, b = 3.14159), Uniform(a = -3.14159, b = 3.14159), IndependentCopula(dimension = 3))

Then we create the multivariate basis onto which the function is expanded. By default, it is associated with the linear enumeration rule. Since our marginals are uniform, the OrthogonalProductPolynomialFactory class produces Legendre polynomials. In order to create the multivariate basis of polynomials, we must specify the number of functions in the basis. In this particular case, we compute that number depending on the total degree. The getMaximumDegreeStrataIndex() method of the enumeration function computes the number of layers necessary to achieve that total degree. Then the number of functions up to that layer is computed with the getStrataCumulatedCardinal() method.

dimension = im.inputDistribution.getDimension()
multivariateBasis = ot.OrthogonalProductPolynomialFactory(
    [im.inputDistribution.getMarginal(i) for i in range(dimension)]
)

totalDegree = 5  # Polynomial degree
enumerate_function = multivariateBasis.getEnumerateFunction()
strataIndex = enumerate_function.getMaximumDegreeStrataIndex(totalDegree)
print("strataIndex = ", strataIndex)
number_of_terms_in_basis = enumerate_function.getStrataCumulatedCardinal(strataIndex)
print("number_of_terms_in_basis = ", number_of_terms_in_basis)
adaptiveStrategy = ot.FixedStrategy(multivariateBasis, number_of_terms_in_basis)
print(adaptiveStrategy)

strataIndex =  5
number_of_terms_in_basis =  56
class=FixedStrategy derived from class=AdaptiveStrategyImplementation maximumDimension=56

We compute the coefficients using a multivariate tensor product Gaussian quadrature rule. Since the coefficients are computed in the standardized space, we first use the getMeasure method of the multivariate basis in order to get that standardized distribution. Then we use the GaussProductExperiment class to create the quadrature, using 6 nodes on each of the dimensions.

standard_distribution = multivariateBasis.getMeasure()
print(standard_distribution)

marginal_number_of_nodes = 6
dim_input = im.model.getInputDimension()
marginalDegrees = [marginal_number_of_nodes] * dim_input
experiment = ot.GaussProductExperiment(im.inputDistribution, marginalDegrees)
X, W = experiment.generateWithWeights()
Y = im.model(X)
print("Sample size = ", X.getSize())

JointDistribution(Uniform(a = -1, b = 1), Uniform(a = -1, b = 1), Uniform(a = -1, b = 1), IndependentCopula(dimension = 3))
Sample size =  216

We see that 216 nodes are involved in this quadrature rule, which is the result of $6^3 = 216$ .

In the next cell, we compute the coefficients of the polynomial chaos expansion using integration.

projectionStrategy = ot.IntegrationStrategy()
chaosalgo = ot.FunctionalChaosAlgorithm(
    X, W, Y, im.inputDistribution, adaptiveStrategy, projectionStrategy
)
chaosalgo.run()
result = chaosalgo.getResult()

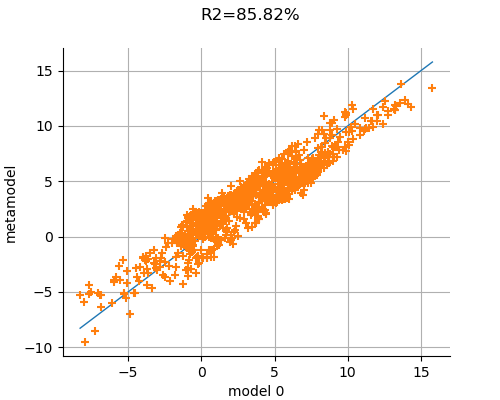
We now validate the metamodel by drawing the validation graph. We see that many points are close to the red test line, which indicates that the predictions of the polynomial chaos expansion are close to the output observations from the model.

view = draw_polynomial_chaos_validation(result, im.model, im.inputDistribution)

In order to have a closer look on the result, we use the printCoefficientsTable function in order to print the first 10 coefficients.

printCoefficientsTable(result)

Total number of coefficients :  56
# Indice, Multi-indice, Degree : Value
#0, [0,0,0] (0) : 3.5049783626206317
#1, [1,0,0] (1) : 1.6254291279668378
#2, [0,1,0] (1) : 9.189697613987136e-16
#3, [0,0,1] (1) : -1.7737547541862853e-16
#4, [2,0,0] (2) : -2.7590776885411117e-15
#5, [1,1,0] (2) : -6.375108774214766e-16
#6, [1,0,1] (2) : -1.8240617349896127e-15
#7, [0,2,0] (2) : -0.6413919098131448
#8, [0,1,1] (2) : -5.117434254131581e-17
#9, [0,0,2] (2) : -1.4085954624931674e-15
#10, [3,0,0] (3) : -1.2911039486376805

We see that there are 56 coefficients in the metamodel and that many of these coefficients are close to zero.

If we print only coefficients greater than $10^{-14}$ , we see that only a fraction of them are significant and that these significant coefficients have a relatively large polynomial degree.

printCoefficientsTable(result, threshold=1.0e-14)

Total number of coefficients :  56
# Indice, Multi-indice, Degree : Value
#0, [0,0,0] (0) : 3.5049783626206317
#1, [1,0,0] (1) : 1.6254291279668378
#7, [0,2,0] (2) : -0.6413919098131448
#10, [3,0,0] (3) : -1.2911039486376805
#15, [1,0,2] (3) : 1.3724300360555144
#30, [0,4,0] (4) : -1.6122740106725177
#35, [5,0,0] (5) : 0.20760614724812593
#40, [3,0,2] (5) : -1.0901427864755082
#49, [1,0,4] (5) : 0.40917958066434623

The previous experiments suggest to keep only the coefficients which are significant in the model: this is the topic of the next section.

Use a model selection method¶

The CleaningStrategy has the following algorithm. On input, it considers only the first maximumConsideredTerms coefficients $a_{\vect{\alpha}}$ . On output it selects the mostSignificant most significant coefficients. To do this, it uses the significanceFactor parameter.

The following function will help to create a sparse PCE using the CleaningStrategy. It takes into account the number of considered coefficients in the expansion, the number of significant coefficients to keep and the relative factor and returns the $R^2$ score.

def compute_cleaning_PCE(
    maximumConsideredTerms, mostSignificant, significanceFactor, verbose=False
):
    """
    Compute a PCE using CleaningStrategy.

    Parameters
    ----------
    maximumConsideredTerms : int
        The maximum number of coefficients considered by the algorithm during
        intermediate steps.

    mostSignificant : int
        The maximum number of coefficients selected by the algorithm in
        the final PCE.

    significanceFactor : float
        The relative part of any coefficient with respect to the maximum
        coefficient.

    verbose : bool
        If set to True, print intermediate messages.

    Returns
    -------
    R2 : float
        The R2 score
    """
    adaptiveStrategy = ot.CleaningStrategy(
        multivariateBasis,
        maximumConsideredTerms,
        mostSignificant,
        significanceFactor,
    )
    chaosalgo = ot.FunctionalChaosAlgorithm(
        X, W, Y, im.inputDistribution, adaptiveStrategy, projectionStrategy
    )
    chaosalgo.run()
    result = chaosalgo.getResult()
    score_R2 = compute_polynomial_chaos_R2(result, im.model, im.inputDistribution)
    if verbose:
        print("R2 = %.2f%%" % (100.0 * score_R2))
        printCoefficientsTable(result)
    return score_R2

In the next cell, we consider at most 500 coefficients and keep only the 5 most significant coefficients. The factor is set to a relatively low value.

maximumConsideredTerms = 500
mostSignificant = 5
significanceFactor = 1.0e-10
score_R2 = compute_cleaning_PCE(
    maximumConsideredTerms, mostSignificant, significanceFactor, verbose=True
)

R2 = -384.39%
Total number of coefficients :  6
# Indice, Multi-indice, Degree : Value
#0, [0,0,0] (0) : 3.5049783626206317
#1, [11,0,0] (11) : -1.6603684437609167
#2, [12,0,0] (12) : -4.269723903959838
#3, [0,12,0] (12) : -4.133953684206107
#4, [0,0,12] (12) : -4.269723903959839
#5, [5,0,8] (13) : -0.052471216285749106

We see that when we keep only 5 coefficients among the first 500 ones, these coefficients have a very high polynomial degree. Indeed, it occurs that these poorly estimated coefficients have a high absolute value. Hence, the criteria selects them as significant coefficients, which leads to a poor metamodel.

Let us reduce the number of considered coefficients and increase the number of selected coefficients.

maximumConsideredTerms = 56
mostSignificant = 10
significanceFactor = 1.0e-10
score_R2 = compute_cleaning_PCE(
    maximumConsideredTerms, mostSignificant, significanceFactor, verbose=True
)

R2 = 85.75%
Total number of coefficients :  9
# Indice, Multi-indice, Degree : Value
#0, [0,0,0] (0) : 3.5049783626206317
#1, [1,0,0] (1) : 1.6254291279668378
#2, [0,2,0] (2) : -0.6413919098131448
#3, [3,0,0] (3) : -1.2911039486376805
#4, [1,0,2] (3) : 1.3724300360555144
#5, [0,4,0] (4) : -1.6122740106725177
#6, [5,0,0] (5) : 0.20760614724812593
#7, [3,0,2] (5) : -1.0901427864755082
#8, [1,0,4] (5) : 0.40917958066434623

When we keep only 10 coefficients among the first 56 ones, the polynomial chaos metamodel is much better: the coefficients are associated with a low polynomial degree, so that the quadrature rule estimates them with greater accuracy.

We would like to know which combination is the best. In the following loop, we consider the maximum number of considered coefficients from 1 to 500 and the number of selected coefficients from 1 to 30. In order to produce the combinations, we use the product function from the itertools module. For each combination, we compute the $R^2$ score and select the combination with the highest $R^2$ coefficient. As shown in [muller2016] page 268, the computed $R^2$ may be optimistic, but this is not the point of the current example.

maximumConsideredTerms_list = list(range(1, 500, 50))
mostSignificant_list = list(range(1, 30, 5))
iterator = itertools.product(maximumConsideredTerms_list, mostSignificant_list)
best_R2_score = 0.0
best_parameters = []
for it in iterator:
    maximumConsideredTerms, mostSignificant = it
    score_R2 = compute_cleaning_PCE(
        maximumConsideredTerms, mostSignificant, significanceFactor
    )
    if score_R2 > best_R2_score:
        best_R2_score = score_R2
        best_parameters = [maximumConsideredTerms, mostSignificant]

print("Best R2 = %.2f%%" % (100.0 * best_R2_score))

maximumConsideredTerms, mostSignificant = best_parameters
print("Number of considered coefficients : ", maximumConsideredTerms)
print("Number of selected coefficients : ", mostSignificant)

Best R2 = 86.15%
Number of considered coefficients :  101
Number of selected coefficients :  16

We see that the best solution could be to select at most 16 significant coefficients among the first 101 ones. Let us see the $R^2$ score and the coefficients in this situation.

score_R2 = compute_cleaning_PCE(
    maximumConsideredTerms, mostSignificant, significanceFactor, verbose=True
)

R2 = 86.15%
Total number of coefficients :  12
# Indice, Multi-indice, Degree : Value
#0, [0,0,0] (0) : 3.5049783626206317
#1, [1,0,0] (1) : 1.6254291279668378
#2, [0,2,0] (2) : -0.6413919098131448
#3, [3,0,0] (3) : -1.2911039486376805
#4, [1,0,2] (3) : 1.3724300360555144
#5, [0,4,0] (4) : -1.6122740106725177
#6, [5,0,0] (5) : 0.20760614724812593
#7, [3,0,2] (5) : -1.0901427864755082
#8, [1,0,4] (5) : 0.40917958066434623
#9, [7,0,0] (7) : -0.2077986425581342
#10, [5,0,2] (7) : 0.1752921165560066

These parameters lead to a total number of coefficients equal to 12. Among the 16 most significant coefficients, only 12 satisfy the criteria. Most of the coefficients have a small polynomial degree although some have a total degree as large as 7.

Intermediate steps of the algorithm¶

If we set the verbose optional input argument of the compute_cleaning_PCE function to True, then intermediate messages are printed in the Terminal. For each step of the adaptivity algorithm, the code prints some of the internal parameters of the algorithm. The data structure uses several variables that we now describe.

Psi_k_p_ : the collection of functions in the current active polynomial multi-index set,
I_p_ : the list of indices of the selected coefficients based according to the enumeration rule,
addedPsi_k_ranks_ : the list of indices to add the multi-index set,
removedPsi_k_ranks_ : the list of indices to remove to the multi-index set,
conservedPsi_k_ranks_ : the index of the first polynomial in the selected multi-index set,
currentVectorIndex_ : the current value of the index in the full multi-index set, according to the enumeration rule.

Each time the selection method is called, it is passed a coefficient $a_{\vect{\alpha}}$ which is a new candidate to be considered by the algorithm. The first time the method is evaluated, the active multi-index set is empty, so that it must be filled with the first coefficients in the multi-index set, according to the enumeration rule. The second time (and up to the end of the algorithm), the candidate coefficient is considered to be added to the multi-index set.

Executing the function prints messages that we can process to produce the following listing. On each step, we print the list of integers corresponding to the indices of the coefficients in the active multi-index set.

Step 1:  [0, 1, 7, 10, 15, 16]
Step 2:  [0, 1, 7, 10, 15, 17]
Step 3:  [0, 1, 7, 10, 15, 18]
Step 4:  [0, 1, 7, 10, 15, 19]
Step 5:  [0, 1, 7, 10, 15, 20]
Step 6:  [0, 1, 7, 10, 15, 21]
Step 7:  [0, 1, 7, 10, 15, 22]
Step 8:  [0, 1, 7, 10, 15, 23]
Step 9:  [0, 1, 7, 10, 15, 24]
Step 10: [0, 1, 7, 10, 15, 25]
[...]
Step 15: [0, 1, 7, 10, 15, 30]
Step 16: [0, 1, 7, 10, 15, 30, 31]
[...]
Step 20: [0, 1, 7, 10, 15, 30, 35]
Step 21: [0, 1, 7, 10, 15, 30, 35, 36]
[...]
Step 25: [0, 1, 7, 10, 15, 30, 35, 40]
Step 26: [0, 1, 7, 10, 15, 30, 35, 40, 41]
[...]
Step 34: [0, 1, 7, 10, 15, 30, 35, 40, 49]
Step 35: [0, 1, 7, 10, 15, 30, 35, 40, 49, 50]
[...]
Step 69: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84]
Step 70: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 85]
[...]
Step 74: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89]
Step 75: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 90]
[...]
Step 83: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 98]
Step 84: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 98, 99]
Step 85: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 98, 100]
Step 86: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 98]
Step 87: [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 98]

The previous text (and a detailed analysis of the output file) allows one to understand what exactly happens in the algorithm. To understand each step, note that the significant threshold is equal to $\epsilon = 10^{-10}$ .

During the initialization, the initial basis is empty and filled with the indices [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. The coefficient with index equal to 0 corrresponds to the mean of the polynomial chaos expansion. As a result, we always want to select that coefficient in the active set. Hence, the calculation of the largest coefficient in absolute value is performed from the indices from 1 to 15. The largest coefficient in absolute value is $a_1 = 1.625$ , which leads to the threshold $\epsilon |a_1| = 1.625 \times 10^{-10}$ . Most of the considered coefficient are, however, too close to zero. This is why only the coefficients [0, 1, 7, 10, 15] are kept in the basis. The corresponding coefficients are [3.505, 1.625,-0.6414, -1.291, 1.372].
On step 1, the candidate index 16 is considered. Its coefficient is $a_{16} = -1.197 \times 10^{-15}$ , which is much too low to be selected. Hence, the basis is unchanged and the active multi-index set is [0, 1, 7, 10, 15] on the end of this step.
From the step 3 to the step 15, the active multi-index set is unchanged, because no considered coefficient becomes greater than the threshold.
On step 16, the candidate index 30 is considered, with corresponding coefficient $a_{30} = -1.612$ . Since this coefficient has an absolute value greater than the threshold, it gets selected and the active multi-index set is [0, 1, 7, 10, 15, 30] on the end of this step. From this step to the end, the index 30 will not leave the active set.
On the step 20, the index 35 enters the active set.
On the step 25, the index 40 enters the active set.
On the step 34, the index 49 enters the active set.
On the step 69, the index 84 enters the active set.
On the step 74, the index 89 enters the active set.
On the step 83, the index 98 enters the active set.
On the last step, the active multi-index set contains the indices [0, 1, 7, 10, 15, 30, 35, 40, 49, 84, 89, 98] and the corresponding coefficients are [3.508, 1.625, -0.6414, -1.291, 1.372, -1.613, 0.2076, -1.090, 0.4092, -0.2078, 0.1753, -0.3250].

We see that the algorithm was able so select 12 coefficients in the first 101 coefficients considered by the algorithm. It could have selected more coefficients since we provided 16 slots to fill thanks to the mostSignificant parameter. The considered coefficients were, however, too close to zero and were below the threshold.

Conclusion¶

We see that the CleaningStrategy class performs correctly in this particular case. We have seen how to select the hyperparameters which produce the best $R^2$ score.

Total running time of the script: (0 minutes 2.266 seconds)

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page