The Branin test case¶

Introduction¶

The Branin function is defined in 2 dimensions based on the functions $g$ :

$g(u_1, u_2) = \frac{\left(u_2-5.1\frac{u_1^2}{4\pi^2}+5\frac{u_1}{\pi}-6\right)^2+10\left(1-\frac{1}{8 \pi}\right) \cos(u_1)+10-54.8104}{51.9496}$

and $t$ :

t(x_1, x2) = (15 x_1 - 5, 15 x_2)^T.

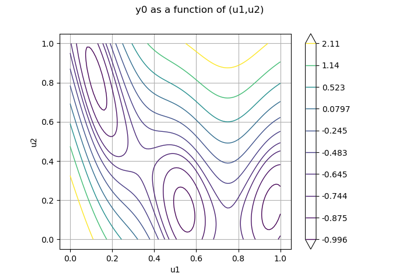
Finally, the Branin function is the composition of the two previous functions:

$f_{Branin}(x_1, x_2) = g \circ t(x_1, x_2)$

for any $\mathbf{x} \in [0, 1]^2$ .

There are three global minimas:

$\mathbf{x}^\star=(0.123895, 0.818329),$

$\mathbf{x}^\star=(0.542773, 0.151666),$

and :

$\mathbf{x}^\star=(0.961652, 0.165000)$

where the function value is:

$f_{min} = f_{Branin}(\mathbf{x}^\star) = -0.97947643837.$

We assume that the output of the Branin function is noisy, with a gaussian noise. In other words, the objective function is:

$f(x_1, x_2) = f_{Branin}(x_1, x_2) + \epsilon$

where $\epsilon$ is a Gaussian random variable with null mean and standard deviation $\sigma_{\epsilon} = 0.1$ .

Dixon, L. C. W., & Szego, G. P. (1978). The global optimization problem: an introduction. Towards global optimization, 2, 1-15.
Forrester, A., Sobester, A., & Keane, A. (2008). Engineering design via surrogate modelling: a practical guide. Wiley.
Global Optimization Test Problems. Retrieved June 2013, from http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO.htm.
Molga, M., & Smutnicki, C. Test functions for optimization needs (2005), from https://robertmarks.org/Classes/ENGR5358/Papers/functions.pdf.
Picheny, V., Wagner, T., & Ginsbourger, D. (2012). A benchmark of kriging-based infill criteria for noisy optimization.

class BraninModel

Data class for the Branin test function.

Attributes:

Examples

>>> from openturns.usecases import branin_function
>>> # Load the Branin model
>>> bm = branin_function.BraninModel()