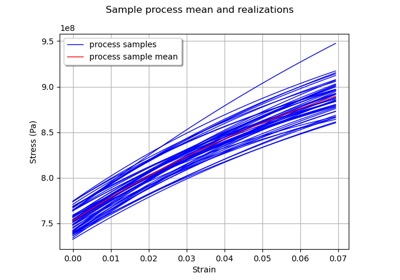
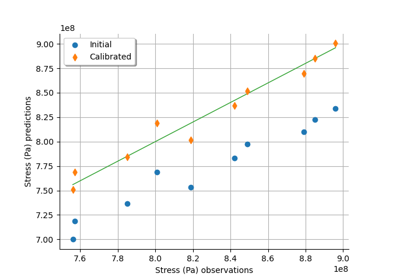
The Chaboche mechanical model

Deterministic model

The Chaboche mechanical law predicts the stress depending on the strain:

\sigma = G(\epsilon,R,C,\gamma) = R + \frac{C}{\gamma} (1-\exp(-\gamma\epsilon))

where:

  • \epsilon is the strain,

  • \sigma is the stress (Pa),

  • R, C, \gamma are the parameters.

The variables have the following distributions and are supposed to be independent.

Random var.

Distribution

R

Lognormal (\mu = 750 MPa, \sigma = 11 MPa)

C

Normal (\mu = 2750 MPa, \sigma = 250 MPa)

\gamma

Normal (\mu = 10, \sigma = 2)

\epsilon

Uniform(a=0, b=0.07).

The model can be used in two different contexts:

  • model calibration with observations where R, C and \gamma are parameters,

  • uncertainty propagation where R, C and \gamma are random variables.

Thanks to

  • Antoine Dumas, Phimeca

References

    1. Lemaitre and J. L. Chaboche (2002) “Mechanics of solid materials” Cambridge University Press.

API documentation

class ChabocheModel(strainMin=0.0, strainMax=0.07, trueR=750000000.0, trueC=2750000000.0, trueGamma=10.0)

Data class for the Chaboche mechanical model.

Parameters:
strainMinfloat, optional

The minimum value of the strain. The default is 0.0.

strainMaxfloat, optional

The maximum value of the strain. The default is 0.07

trueRfloat, optional

The true value of the R parameter. The default is 750.0e6.

trueCfloat, optional

The true value of the C parameter. The default is 2750.0e6.

trueGammafloat, optional

The true value of the Gamma parameter. The default is 10.0.

Attributes:
dimint

Dimension of the problem, dim=4.

StrainUniform distribution

Uniform(strainMin, strainMax)

RLogNormal distribution

LogNormal().setParameter(ot.LogNormalMuSigma()([750.0e6, 11.0e6, 0.0]))

CNormal distribution

Normal(2750.0e6, 250.0e6)

GammaNormal distribution

Normal(10.0, 2.0)

inputDistributionJointDistribution

The joint distribution of the input parameters.

modelFunction

The Chaboche mechanical law. The model has input dimension 4 and output dimension 1. More precisely, we have \vect{X} = (\epsilon, R, C, \gamma) and Y = \sigma.

dataSample

A data set of size 10 and dimension 2 which contains noisy observations of the strain (column 0) and the stress (column 1).

Examples

>>> from openturns.usecases import chaboche_model
>>> # Load the Chaboche model
>>> cm = chaboche_model.ChabocheModel()
>>> print(cm.data[:5])
        [ Strain      Stress (Pa) ]
0 : [ 0           7.56e+08    ]
1 : [ 0.0077      7.57e+08    ]
2 : [ 0.0155      7.85e+08    ]
3 : [ 0.0233      8.19e+08    ]
4 : [ 0.0311      8.01e+08    ]
>>> print("Inputs:", cm.model.getInputDescription())
Inputs: [Strain,R,C,Gamma]
>>> print("Outputs:", cm.model.getOutputDescription())
Outputs: [Sigma]

Examples based on this use case

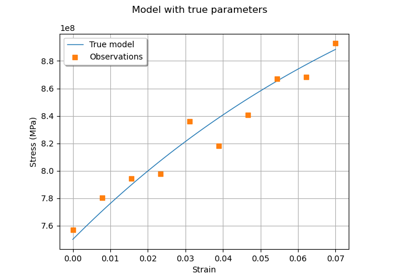
Create a process sample from a sample

Create a process sample from a sample

Generate observations of the Chaboche mechanical model

Generate observations of the Chaboche mechanical model

Calibration of the Chaboche mechanical model

Calibration of the Chaboche mechanical model