Vertical deflection of a tube

Description

We consider the deflection of a tube under a vertical stress.

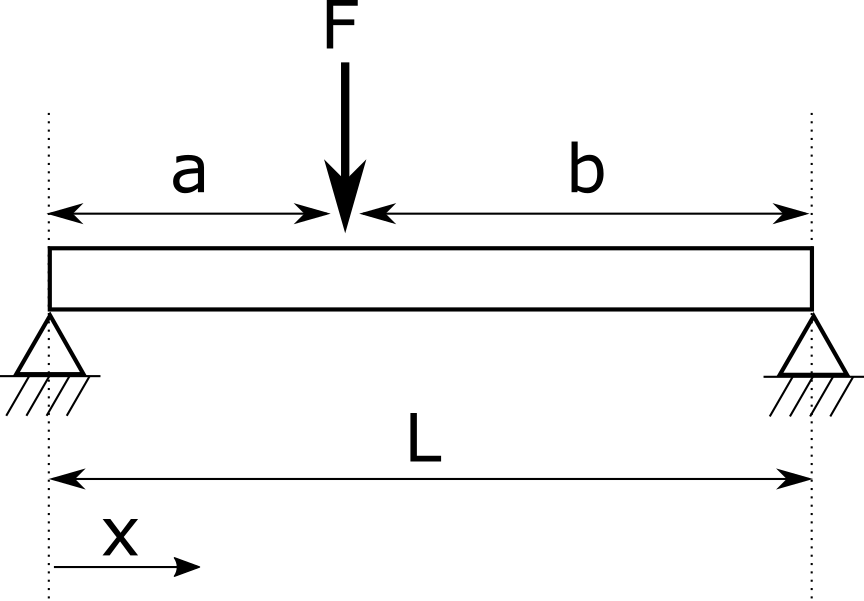
A simply supported beam

The parameters of the model are:

• F : the strength,

• L : the length of the tube,

• a : position of the force,

• D : external diameter of the tube,

• d : internal diameter of the tube,

• E : Young modulus.

The following figure presents the internal and external diameter of the tube:

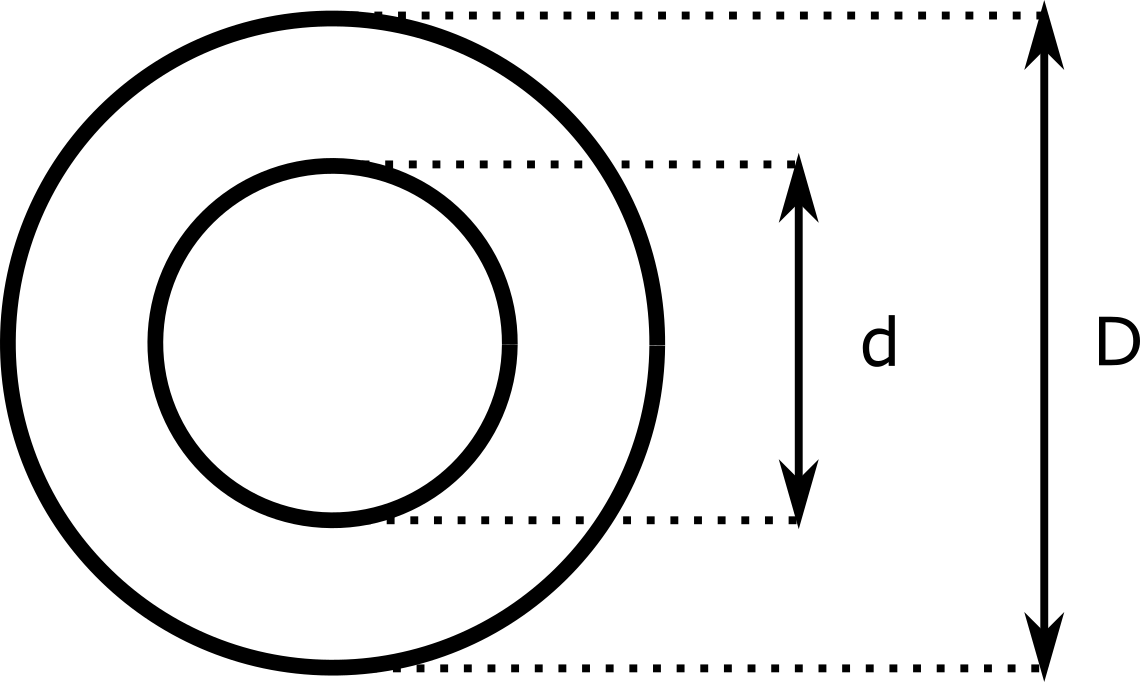
Tube diameters

The area moment of inertia of the cross section about the neutral axis of a round tube (i.e. perpendicular to the section) with external and internal diameters and are:

The vertical deflection at point is:

where . The angle of the tube at the left end is:

and the angle of the tube at the right end is:

The following table presents the distributions of the random variables. These variables are assumed to be independent.

Variable	Distribution
F	Normal(1,0.1)
L	Normal(1.5,0.01)
a	Uniform(0.7,1.2)
D	Triangular(0.75,0.8,0.85)
d	Triangular(0.09,0.1,0.11)
E	Normal(200000,2000)

References

• Deflection of beams by Russ Elliott. http://www.clag.org.uk/beam.html

• https://upload.wikimedia.org/wikipedia/commons/f/ff/Simple_beam_with_offset_load.svg

• https://en.wikipedia.org/wiki/Deflection_(engineering)

• https://mechanicalc.com/reference/beam-deflection-tables

• https://en.wikipedia.org/wiki/Second_moment_of_area

• Shigley’s Mechanical Engineering Design (9th Edition), Richard G. Budynas, J. Keith Nisbettn, McGraw Hill (2011)

• Mechanics of Materials (7th Edition), James M. Gere, Barry J. Goodno, Cengage Learning (2009)

• Statics and Mechanics of Materials (5th Edition), Ferdinand Beer, E. Russell Johnston, Jr., John DeWolf, David Mazurek. Mc Graw Hill (2011) Chapter 15: deflection of beams.

API documentation

class DeflectionTube

Data class for the deflection of a tube model.

Attributes:

dimint

The dimension of the problem: dim=6

modelSymbolicFunction

Model of the deflection. The model has input dimension 6 and output dimension 3. More precisely, we have and .

XFNormal

F distribution Normal(1, 0.1)

XENormal

E distribution Normal(200000, 2000)

XLDirac

L distribution Dirac(1.5)

XaDirac

a distribution Dirac(1.0)

XDDirac

D distribution Dirac(0.8)

XdDirac

d distribution Dirac(0.1)

inputDistributionJointDistribution

The joint distribution of the input parameters.

Examples

>>> from openturns.usecases import deflection_tube
>>> # Load the deflection tube model
>>> dt = deflection_tube.DeflectionTube()
>>> print("Inputs:", dt.model.getInputDescription())
Inputs: [F,L,a,De,di,E]
>>> print("Outputs:", dt.model.getOutputDescription())
[Deflection,Left angle,Right angle]

Examples based on this use case

Calibration of the deflection of a tube

Calibration of the deflection of a tube