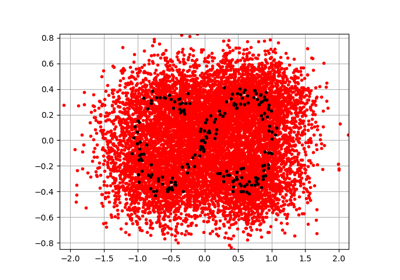
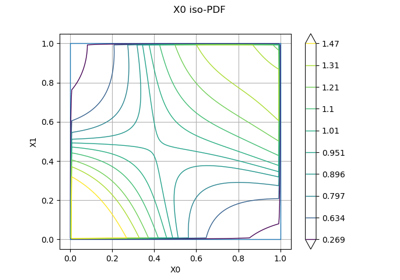
BernsteinCopulaFactory¶

class BernsteinCopulaFactory(*args)¶

EmpiricalBernsteinCopula factory.

Methods

`ComputeAMISEBinNumber`(sample)	Compute the optimal AMISE number of bins.
`ComputeLogLikelihoodBinNumber`(*args)	Compute the optimal log-likelihood number of bins by cross-validation.
`ComputePenalizedCsiszarDivergenceBinNumber`(*args)	Compute the optimal penalized Csiszar divergence number of bins.
`build`(*args)	Build the empirical Bernstein copula.
`buildAsEmpiricalBernsteinCopula`(*args)	Build the empirical Bernstein copula as a native distribution.
`buildEstimator`(*args)	Build the distribution and the parameter distribution.
`getBootstrapSize`()	Accessor to the bootstrap size.
`getClassName`()	Accessor to the object's name.
`getKnownParameterIndices`()	Accessor to the known parameters indices.
`getKnownParameterValues`()	Accessor to the known parameters values.
`getName`()	Accessor to the object's name.
`hasName`()	Test if the object is named.
`setBootstrapSize`(bootstrapSize)	Accessor to the bootstrap size.
`setKnownParameter`(values, positions)	Accessor to the known parameters.
`setName`(name)	Accessor to the object's name.

See also

DistributionFactory, EmpiricalBernsteinCopula

Notes

This class builds an EmpiricalBernsteinCopula which is a non parametric fitting of the copula of a multivariate distribution.

The keys of ResourceMap related to the class are:

the keys BernsteinCopulaFactory-MinM and BernsteinCopulaFactory-MaxM that define the range of $m$ in the optimization problems computing the optimal bin number according to a specified criterion,
the key BernsteinCopulaFactory-BinNumberSelection that defines the criterion to compute the optimal bin number when it is not specified. The possible choices are ‘AMISE’, ‘LogLikelihood’, ‘PenalizedCsiszarDivergence’;
the key BernsteinCopulaFactory-KFraction that defines the fraction of the sample used for the validation in the method ComputeLogLikelihoodBinNumber(),
the key BernsteinCopulaFactory-SamplingSize that defines the $N$ parameter used in the method ComputePenalizedCsiszarDivergenceBinNumber().

__init__(*args)¶

static ComputeAMISEBinNumber(sample)¶

Compute the optimal AMISE number of bins.

Parameters:

sample2-d sequence of float, of dimension 1: The sample from which the optimal AMISE bin number is computed.

Notes

The bin number $m$ is computed by minimizing the asymptotic mean integrated squared error (AMISE), leading to:

$m = 1+\left\lfloor \sampleSize^{\frac{2}{4+d}} \right\rfloor$

where $\lfloor x \rfloor$ is the largest integer less than or equal to $x$ , $\sampleSize$ the sample size and $d$ the sample dimension.

Note that this optimal $m$ does not necessarily divide the sample size $\sampleSize$ .

static ComputeLogLikelihoodBinNumber(*args)¶

Compute the optimal log-likelihood number of bins by cross-validation.

Parameters:

sample2-d sequence of float, of dimension 1

The sample of size $\sampleSize$ from which the optimal log-likelihood bin number is computed.

kFractionint, $0<kFraction<\sampleSize$

The fraction of the sample used for the validation.

Default value 2.

Notes

Let $\cE= (\inputReal_1, \dots, \inputReal_\sampleSize)$ be the given sample. If $kFraction=1$ , the bin number $m$ is given by:

$m = \argmin_{M\in\{1,\dots,\sampleSize\}}\dfrac{1}{\sampleSize}\sum_{\vect{x}_i\in\cE}-\log c^{\cE}_{M}(\vect{x}_i)$

where $c_M^{\cE}$ is the density function of the EmpiricalBernsteinCopula associated to the sample $\cE$ and the bin number $M$ .

If $kFraction>1$ , the bin number $m$ is given by:

$m = \argmin_{M\in\{1,\dots,\sampleSize\}}\dfrac{1}{kFraction}\sum_{k=0}^{kFraction-1}\dfrac{1}{\sampleSize}\sum_{\vect{x}_i\in\cE^V_k}-\log c^{\cE^L_k}_{M}(\vect{x}_i)$

where $\cE^V_k=\left\{\vect{x}_i\in\cE\,|\,i\equiv k \mod kFraction\right\}$ and $\cE^L_k=\cE \backslash \cE^V_k$ .

Note that this optimal $m$ does not necessarily divide the sample size $\sampleSize$ .

static ComputePenalizedCsiszarDivergenceBinNumber(*args)¶

Compute the optimal penalized Csiszar divergence number of bins.

Parameters:

sample2-d sequence of float, of dimension 1: The sample of size $\sampleSize$ from which the optimal AMISE bin number is computed.
fFunction: The function defining the Csiszar divergence of interest.
alphafloat, $\alpha\geq 0$: The penalization factor.

Notes

Let $\cE=(\inputReal_1, \dots, \inputReal_\sampleSize)$ be the given sample. The bin number $m$ is given by:

$m = \argmin_{M\in\{1,\dots,\sampleSize\}}\left[\hat{D}_f(c^{\cE}_{M})-\dfrac{1}{\sampleSize}\sum_{\vect{x}_i\in\cE}f\left(\dfrac{1}{c^{\cE}_{M}(\vect{x}_i)}\right)\right]^2-[\rho_S(c^{\cE}_{M})-\rho_S({\cE}_{M})]^2$

where $c_M^{\cE}$ is the density function of the EmpiricalBernsteinCopula associated to the sample $\cE$ and the bin number $M$ , $\hat{D}_f(c^{\cE}_{M})=\dfrac{1}{N}\sum_{j=1}^Nf\left(\dfrac{1}{\vect{u}_j}\right)$ a Monte Carlo estimate of the Csiszar $f$ divergence, $\rho_S(c^{\cE}_{M})$ the exact Spearman correlation of the empirical Bernstein copula $c^{\cE}_{M}$ and $\rho_S({\cE}_{M})$ the empirical Spearman correlation of the sample ${\cE}_{M}$ .

The parameter $N$ is controlled by the BernsteinCopulaFactory-SamplingSize key in ResourceMap.

Note that this optimal $m$ does not necessarily divide the sample size $\sampleSize$ .

build(*args)¶

Build the empirical Bernstein copula.

Available usages:

build()

build(sample)

build(sample, m)

build(sample, method, f)

Parameters:

sample2-d sequence of float, of dimension $d$

The sample of size $\sampleSize>0$ from which the copula is estimated.

methodstr

The name of the bin number selection method. Possible choices are AMISE, LogLikelihood and PenalizedCsiszarDivergence.

Default is LogLikelihood.

fFunction

The function defining the Csiszar divergence of interest used by the PenalizedCsiszarDivergence method.

Default is Function().

mint,:math:1 leq m leq sampleSize,

The bin number, i.e. the number of sub-intervals in which all the edges of the unit cube $[0, 1]^d$ are regularly partitioned.

Default value is the value computed from the default bin number selection method.

Returns:

copulaDistribution: The empirical Bernstein copula as a generic distribution.

Notes

If the bin number $m$ is specified and does not divide the sample size $\sampleSize$ , then a part of the sample is removed for the result to be a copula. See EmpiricalBernsteinCopula.

buildAsEmpiricalBernsteinCopula(*args)¶

Build the empirical Bernstein copula as a native distribution.

Available usages:

buildAsEmpiricalBernsteinCopula()

buildAsEmpiricalBernsteinCopula(sample)

buildAsEmpiricalBernsteinCopula(sample, m)

buildAsEmpiricalBernsteinCopula(sample, method, f)

Parameters:

sample2-d sequence of float, of dimension d

The sample of size $\sampleSize>0$ from which the copula is estimated.

methodstr

The name of the bin number selection method. Possible choices are AMISE, LogLikelihood and PenalizedCsiszarDivergence.

Default is LogLikelihood.

fFunction

The function defining the Csiszar divergence of interest used by the PenalizedCsiszarDivergence method.

Default is Function().

mint, $1 \leq m \leq \sampleSize$ ,

The bin number, i.e. the number of sub-intervals in which all the edges of the unit cube $[0, 1]^d$ are regularly partitioned.

Default value is the value computed from the default bin number selection method.

Returns:

copulaEmpiricalBernsteinCopula: The empirical Bernstein copula as a native distribution.

Notes

If the bin number $m$ is specified and does not divide the sample size $\sampleSize$ , then a part of the sample is removed for the result to be a copula a copula. See EmpiricalBernsteinCopula.

buildEstimator(*args)¶

Build the distribution and the parameter distribution.

Parameters:

sample2-d sequence of float: Data.
parametersDistributionParameters: Optional, the parametrization.

Returns:

resDistDistributionFactoryResult: The results.

Notes

According to the way the native parameters of the distribution are estimated, the parameters distribution differs:

Moments method: the asymptotic parameters distribution is normal and estimated by Bootstrap on the initial data;

Maximum likelihood method with a regular model: the asymptotic parameters distribution is normal and its covariance matrix is the inverse Fisher information matrix;

Other methods: the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting (see KernelSmoothing).

If another set of parameters is specified, the native parameters distribution is first estimated and the new distribution is determined from it:

if the native parameters distribution is normal and the transformation regular at the estimated parameters values: the asymptotic parameters distribution is normal and its covariance matrix determined from the inverse Fisher information matrix of the native parameters and the transformation;

in the other cases, the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting.

getBootstrapSize()¶

Accessor to the bootstrap size.

Returns:

sizeint: Size of the bootstrap.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getKnownParameterIndices()¶

Accessor to the known parameters indices.

Returns:

indicesIndices: Indices of the known parameters.

getKnownParameterValues()¶

Accessor to the known parameters values.

Returns:

valuesPoint: Values of known parameters.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

setBootstrapSize(bootstrapSize)¶

Accessor to the bootstrap size.

Parameters:

sizeint: The size of the bootstrap.

setKnownParameter(values, positions)¶

Accessor to the known parameters.

Parameters:

valuessequence of float: Values of known parameters.
positionssequence of int: Indices of known parameters.

Examples

When a subset of the parameter vector is known, the other parameters only have to be estimated from data.

In the following example, we consider a sample and want to fit a Beta distribution. We assume that the $a$ and $b$ parameters are known beforehand. In this case, we set the third parameter (at index 2) to -1 and the fourth parameter (at index 3) to 1.

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> distribution = ot.Beta(2.3, 2.2, -1.0, 1.0)
>>> sample = distribution.getSample(10)
>>> factory = ot.BetaFactory()
>>> # set (a,b) out of (r, t, a, b)
>>> factory.setKnownParameter([-1.0, 1.0], [2, 3])
>>> inf_distribution = factory.build(sample)