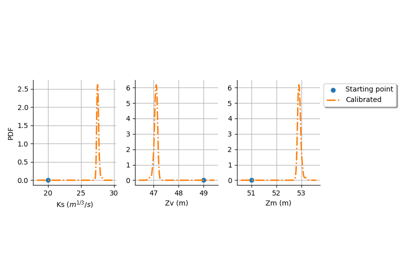
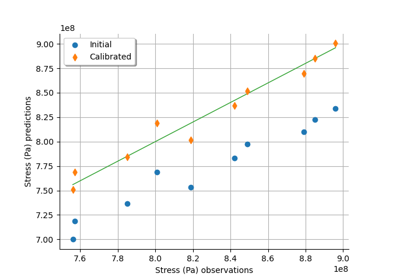
GaussianLinearCalibration

class GaussianLinearCalibration(*args)

Gaussian linear calibration algorithm.

Available constructors:

GaussianLinearCalibration(model, inputObservations, outputObservations, parameterMean, parameterCovariance, errorCovariance, methodName)

GaussianLinearCalibration(modelObservations, gradientObservations, outputObservations, parameterMean, parameterCovariance, errorCovariance, methodName)

Parameters:

modelFunction

The parametric function to be calibrated.

inputObservations2-d sequence of float

The sample of input observations. Can have dimension 0 to specify no observations.

outputObservations2-d sequence of float

The sample of output observations.

parameterMeansequence of float

The mean of the Gaussian prior distribution of the parameter.

parameterCovariance2-d sequence of float

The covariance matrix of the Gaussian prior distribution of the parameter.

errorCovariance2-d sequence of float

The covariance matrix of the Gaussian distribution of the observations error.

methodNamestr

The name of the least-squares method to use for the calibration. By default, equal to QR. Possible values are SVD, QR, Cholesky.

modelObservations2-d sequence of float

The sample of output values of the model.

gradientObservations2-d sequence of float

The Jacobian matrix of the model with respect to the parameter.

Methods

getClassName()	Accessor to the object's name.
getErrorCovariance()	Accessor to the observation error covariance.
getGlobalErrorCovariance()	Accessor to the flag for a global observation error covariance.
getGradientObservations()	Accessor to the model gradient at the parameterMean.
getInputObservations()	Accessor to the input data to be fitted.
getMethodName()	Accessor to the name of least-squares method used for the resolution.
getModel()	Accessor to the model to be fitted.
getModelObservations()	Accessor to the model evaluation at the parameterMean.
getName()	Accessor to the object's name.
getOutputObservations()	Accessor to the output data to be fitted.
getParameterCovariance()	Accessor to the parameter prior covariance.
getParameterMean()	Accessor to the parameter parameterMean.
getParameterPrior()	Accessor to the parameter prior distribution.
getResult()	Get the result structure.
hasName()	Test if the object is named.
run()	Launch the algorithm.
setName(name)	Accessor to the object's name.
setResult(result)	Accessor to optimization result.

See also

LinearLeastSquaresCalibration, NonLinearLeastSquaresCalibration, GaussianNonLinearCalibration

Notes

This class implements the Maximum A Posteriori (MAP) estimator for a linear model under the Bayesian hypothesis that the prior and the observation errors have Gaussian distributions. This is also known as the Kalman filter.

The given observation error covariance can be either local, ie the same matrix applies for each observation and is of dimension the output dimension of the model, or global, ie the matrix describes the full set of observation errors, in which case its dimension is the product of the output dimension of the model and the number of observations.

The prior distribution of the parameter is a Normal.

The posterior distribution of the parameter is Normal.

The resulting error distribution is Normal with a zero mean and with a covariance matrix equal to the errorCovariance input argument.

Please read Gaussian calibration for more details.

Examples

Calibrate a nonlinear model using GaussianLinearCalibration:

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> m = 10
>>> x = [[0.5 + i] for i in range(m)]
>>> inVars = ['a', 'b', 'c', 'x']
>>> formulas = ['a + b * exp(c * x)']
>>> model = ot.SymbolicFunction(inVars, formulas)
>>> p_ref = [2.8, 1.2, 0.5]
>>> params = [0, 1, 2]
>>> modelX = ot.ParametricFunction(model, params, p_ref)
>>> y = modelX(x)
>>> y += ot.Normal(0.0, 0.05).getSample(m)
>>> parameterMean = [1.0]*3
>>> priorCovariance = ot.CovarianceMatrix(3)
>>> errorCovariance = ot.CovarianceMatrix(1, [0.1])
>>> method = 'SVD'
>>> algo = ot.GaussianLinearCalibration(modelX, x, y, parameterMean, priorCovariance, errorCovariance, method)
>>> algo.run()
>>> print(algo.getResult().getParameterMAP())
[8.11483,0.0770992,0.992927]

__init__(*args)

getClassName()

Accessor to the object’s name.

Returns:

class_namestr

The object class name (object.__class__.__name__).

getErrorCovariance()

Accessor to the observation error covariance.

Returns:

errorCovarianceMatrix

Observation error covariance.

getGlobalErrorCovariance()

Accessor to the flag for a global observation error covariance.

Returns:

flagbool

Flag telling if the given observation error covariance is global or not.

getGradientObservations()

Accessor to the model gradient at the parameterMean.

Returns:

gradientObservationMatrix

Gradient of the model at the parameterMean point.

getInputObservations()

Accessor to the input data to be fitted.

Returns:

dataSample

The input data to be fitted.

getMethodName()

Accessor to the name of least-squares method used for the resolution.

Returns:

namestr

Name of least-squares method used for the resolution.

getModel()

Accessor to the model to be fitted.

Returns:

dataFunction

The model to be fitted.

getModelObservations()

Accessor to the model evaluation at the parameterMean.

Returns:

modelObservationSample

Evaluation of the model at the parameterMean point.

getName()

Accessor to the object’s name.

Returns:

namestr

The name of the object.

getOutputObservations()

Accessor to the output data to be fitted.

Returns:

dataSample

The output data to be fitted.

getParameterCovariance()

Accessor to the parameter prior covariance.

Returns:

priorCovarianceMatrix

Parameter prior covariance.

getParameterMean()

Accessor to the parameter parameterMean.

Returns:

parameterMeanPoint

Parameter parameterMean.

getParameterPrior()

Accessor to the parameter prior distribution.

Returns:

priorDistribution

The parameter prior distribution.

getResult()

Get the result structure.

Returns:

resCalibrationCalibrationResult

The structure containing all the results of the calibration problem.

Notes

The structure contains all the results of the calibration problem.

hasName()

Test if the object is named.

Returns:

hasNamebool

True if the name is not empty.

run()

Launch the algorithm.

Notes

It launches the algorithm and creates a CalibrationResult, structure containing all the results.

setName(name)

Accessor to the object’s name.

Parameters:

namestr

The name of the object.

setResult(result)

Accessor to optimization result.

Parameters:

resultCalibrationResult

Result class.

Examples using the class

Calibration of the flooding model

Calibration of the flooding model

Calibration of the Chaboche mechanical model

Calibration of the Chaboche mechanical model