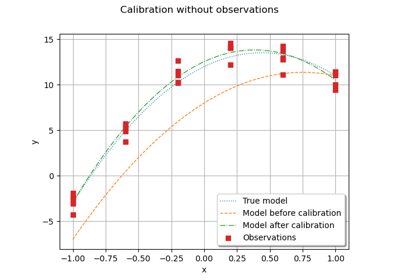
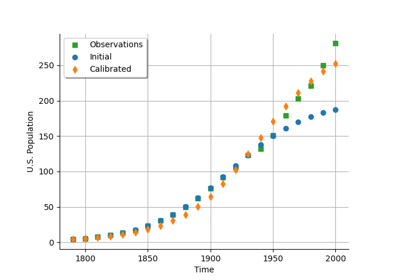
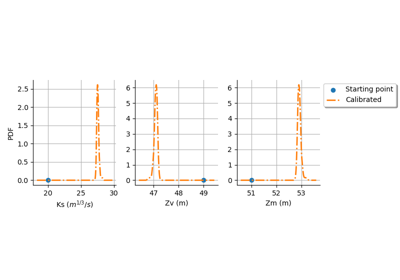
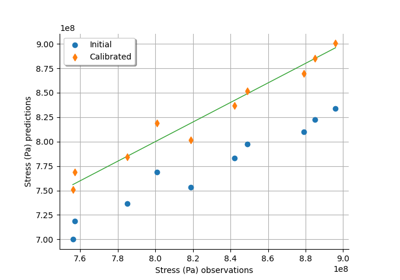
LinearLeastSquaresCalibration

class LinearLeastSquaresCalibration(*args)

Linear least squares calibration algorithm.

Available constructors:

LinearLeastSquaresCalibration(model, inputObservations, outputObservations, startingPoint, methodName)

LinearLeastSquaresCalibration(modelObservations, gradientObservations, outputObservations, startingPoint, methodName)

Parameters:

modelFunction

The parametric function to be calibrated.

inputObservations2-d sequence of float

The sample of input observations. Can have dimension 0 to specify no observations.

outputObservations2-d sequence of float

The sample of output observations.

startingPointsequence of float

The reference value of the parameter, where the linearization of the parametric model is evaluated.

methodNamestr

The name of the least-squares method to use for the calibration. By default, equal to QR. Possible values are SVD, QR, Cholesky.

modelObservations2-d sequence of float

The sample of output values of the model.

gradientObservations2-d sequence of float

The Jacobian matrix of the model with respect to the parameter.

Methods

getClassName()	Accessor to the object's name.
getGradientObservations()	Accessor to the model gradient at the startingPoint.
getInputObservations()	Accessor to the input data to be fitted.
getMethodName()	Accessor to the name of least-squares method used for the resolution.
getModel()	Accessor to the model to be fitted.
getModelObservations()	Accessor to the model evaluation at the startingPoint.
getName()	Accessor to the object's name.
getOutputObservations()	Accessor to the output data to be fitted.
getParameterPrior()	Accessor to the parameter prior distribution.
getResult()	Get the result structure.
getStartingPoint()	Accessor to the parameter startingPoint.
hasName()	Test if the object is named.
run()	Launch the algorithm.
setName(name)	Accessor to the object's name.
setResult(result)	Accessor to optimization result.

See also

GaussianLinearCalibration, NonLinearLeastSquaresCalibration, GaussianNonLinearCalibration

Notes

LinearLeastSquaresCalibration is the minimum variance estimator of the parameter of a given model under the assumption that this parameter acts linearly in the model.

The prior distribution of the parameter is a noninformative prior emulated using a flat Normal centered on the startingPoint and with a variance equal to SpecFunc.Infinity.

The posterior distribution of the parameter is Normal and reflects the variability of the optimum parameter depending on the observation sample. The associated covariance matrix may be regularized depending on the value of the key LinearLeastSquaresCalibration-Regularization in the ResourceMap. Let us denote by the largest singular value of the covariance matrix. The default value of the LinearLeastSquaresCalibration-Regularization, zero, ensures that the singular values of the covariance matrix are left unmodified. If this parameter is set to a nonzero, relatively small, value denoted by , then all singular values of the covariance matrix are increased by .

The resulting distribution of the output error is Normal with a zero mean and a diagonal covariance matrix computed from the residuals. The residuals are computed based on the linearization of the model, where the Jacobian matrix is evaluated at the startingPoint. The diagonal of the covariance matrix of the output error is constant and is estimated with the unbiased variance estimator.

Please read Code calibration for more details.

Examples

Calibrate a nonlinear model using linear least-squares:

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> m = 10
>>> x = [[0.5 + i] for i in range(m)]
>>> inVars = ['a', 'b', 'c', 'x']
>>> formulas = ['a + b * exp(c * x)']
>>> model = ot.SymbolicFunction(inVars, formulas)
>>> p_ref = [2.8, 1.2, 0.5]
>>> params = [0, 1, 2]
>>> modelX = ot.ParametricFunction(model, params, p_ref)
>>> y = modelX(x)
>>> y += ot.Normal(0.0, 0.05).getSample(m)
>>> startingPoint = [1.0]*3
>>> method = 'SVD'
>>> algo = ot.LinearLeastSquaresCalibration(modelX, x, y, startingPoint, method)
>>> algo.run()
>>> print(algo.getResult().getParameterMAP())
[8.24019,0.0768046,0.992957]

__init__(*args)

getClassName()

Accessor to the object’s name.

Returns:

class_namestr

The object class name (object.__class__.__name__).

getGradientObservations()

Accessor to the model gradient at the startingPoint.

Returns:

gradientObservationMatrix

Gradient of the model at the startingPoint point.

getInputObservations()

Accessor to the input data to be fitted.

Returns:

dataSample

The input data to be fitted.

getMethodName()

Accessor to the name of least-squares method used for the resolution.

Returns:

namestr

Name of least-squares method used for the resolution.

getModel()

Accessor to the model to be fitted.

Returns:

dataFunction

The model to be fitted.

getModelObservations()

Accessor to the model evaluation at the startingPoint.

Returns:

modelObservationSample

Evaluation of the model at the startingPoint.

getName()

Accessor to the object’s name.

Returns:

namestr

The name of the object.

getOutputObservations()

Accessor to the output data to be fitted.

Returns:

dataSample

The output data to be fitted.

getParameterPrior()

Accessor to the parameter prior distribution.

Returns:

priorDistribution

The parameter prior distribution.

getResult()

Get the result structure.

Returns:

resCalibrationCalibrationResult

The structure containing all the results of the calibration problem.

Notes

The structure contains all the results of the calibration problem.

getStartingPoint()

Accessor to the parameter startingPoint.

Returns:

startingPointPoint

Parameter startingPoint.

hasName()

Test if the object is named.

Returns:

hasNamebool

True if the name is not empty.

run()

Launch the algorithm.

Notes

It launches the algorithm and creates a CalibrationResult, structure containing all the results.

setName(name)

Accessor to the object’s name.

Parameters:

namestr

The name of the object.

setResult(result)

Accessor to optimization result.

Parameters:

resultCalibrationResult

Result class.

Examples using the class

Calibration without observed inputs

Calibration without observed inputs

Calibration of the logistic model

Calibration of the logistic model

Calibration of the flooding model

Calibration of the flooding model

Calibration of the Chaboche mechanical model

Calibration of the Chaboche mechanical model