IteratedQuadrature¶
(Source code, png)
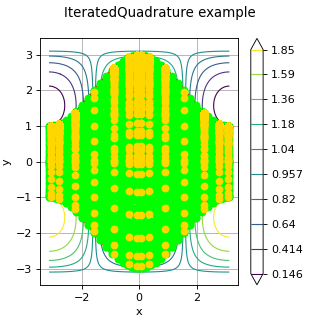
- class IteratedQuadrature(*args)¶
Multivariate integration algorithm.
- Parameters:
- univariateQuadrature
IntegrationAlgorithm By default, the integration algorithm is the Gauss-Kronrod algorithm (
GaussKronrod) with the parameters IteratedQuadrature-MaximumSubIntervals, IteratedQuadrature-MaximumError, IteratedQuadrature-Rule inResourceMap.
- univariateQuadrature
Methods
Accessor to the underlying 1D integration algorithm.
Accessor to the object's name.
getName()Accessor to the object's name.
hasName()Test if the object is named.
integrate(*args)Evaluation of the integral of
on a domain.
setAlgorithm(algorithm)Set the underlying 1D integration algorithm.
setName(name)Accessor to the object's name.
Notes
This class enables to approximate the following integral:
with
,
and
. For
, there is no bound functions
and
.
Note that the default parametrisation of the
GaussKronrodclass leads to a more precise evaluation of the integral but at a greater cost.It is recommended to increase the order of the quadrature rule and the number of subintervals if the integrand or one of the bound functions is smooth but with many oscillations.
When the function
has a scalar input, use the iterated quadrature algorithm of the
GaussKronrodclass.Examples
Create an iterated quadrature algorithm:
>>> import openturns as ot >>> import math as m >>> a = -m.pi >>> b = m.pi >>> f = ot.SymbolicFunction(['x', 'y'], ['1+cos(x)*sin(y)']) >>> l = [ot.SymbolicFunction(['x'], [' 2+cos(x)'])] >>> u = [ot.SymbolicFunction(['x'], ['-2-cos(x)'])]
Evaluate the integral with high precision:
>>> Iref = ot.IteratedQuadrature(ot.GaussKronrod(100000, 1e-13, ot.GaussKronrodRule(ot.GaussKronrodRule.G11K23))).integrate(f, a, b, l, u)
Evaluate the integral with the default IteratedQuadrature algorithm:
>>> Idefault = ot.IteratedQuadrature().integrate(f, a, b, l, u) >>> relative_error = abs(1.0-Idefault[0]/Iref[0])
- __init__(*args)¶
- getAlgorithm()¶
Accessor to the underlying 1D integration algorithm.
- Returns:
- algo
IntegrationAlgorithm The 1D integration algorithm used recursively over the dimensions of the integration domain.
- algo
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- integrate(*args)¶
Evaluation of the integral of
on a domain.
- Available usages:
integrate(f, interval)
integrate(f, a, b, lowerBoundFunctions, upperBoundFunctions)
- Parameters:
- f
Function, The integrand function.
- interval
Interval, The integration domain.
- a,bfloat
Bounds of the integration interval of the first scalar input
- lowerBoundFunctions, upperBoundFunctionslist of
Function List of
functions
and
where
defining the integration domain as defined above. The bound functions can cross each other.
- f
- Returns:
- value
Point Approximation of the integral.
- value
- setAlgorithm(algorithm)¶
Set the underlying 1D integration algorithm.
- Parameters:
- algo
IntegrationAlgorithm The 1D integration algorithm used recursively over the dimensions of the integration domain.
- algo
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
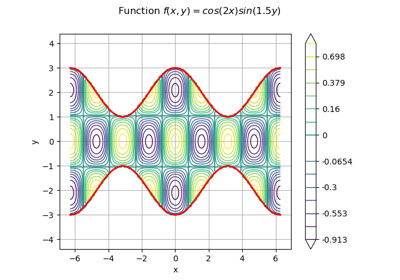
Estimate a multivariate integral with IteratedQuadrature
 OpenTURNS
OpenTURNS