GaussKronrod¶

(Source code, png)

class GaussKronrod(*args)¶

Adaptive integration algorithm of Gauss-Kronrod.

Parameters:

maximumSubIntervalsint: The maximal number of subdivisions of the interval $[a,b]$
maximumErrorfloat: The maximal error between Gauss and Kronrod approximations.
GKRuleGaussKronrodRule: The rule that fixes the number of points used in the Gauss and Kronrod approximations.

Methods

`GetRuleFromName`(name)	Get the integration rule corresponding to the given name.
`GetRules`()	Get the collection of available integration rules.
`getClassName`()	Accessor to the object's name.
`getMaximumError`()	Accessor to the maximal error between Gauss and Kronrod approximations.
`getMaximumSubIntervals`()	Accessor to the maximal number of subdivisions of $[a,b]$ .
`getName`()	Accessor to the object's name.
`getRule`()	Accessor to the Gauss-Kronrod rule used in the integration algorithm.
`hasName`()	Test if the object is named.
`integrate`(*args)	Evaluation of the integral of $f$ on an interval.
`setMaximumError`(maximumError)	Set the maximal error between Gauss and Kronrod approximations.
`setMaximumSubIntervals`(maximumSubIntervals)	Set the maximal number of subdivisions of $[a,b]$ .
`setName`(name)	Accessor to the object's name.
`setRule`(rule)	Set the Gauss-Kronrod rule used in the integration algorithm.

Notes

We consider a function $f: \Rset \mapsto \Rset^\outputDim$ and a domain $\set{D} = [a,b]$ where $a,b \in \Rset$ .The Gauss-Kronrod algorithm approximates the definite integral:

(1)¶ $\int_{a}^b f(t)\di{t}$

using both Gauss and Kronrod approximations, using the rule defined in GaussKronrodRule.

The Gauss-Kronrod algorithm evaluates the integral using the Gauss and the Konrod approximations. If the difference between both approximations is larger that maximumError, then the interval $[a,b]$ is subdivided into 2 subintervals with the same length. The Gauss-Kronrod algorithm is then applied on both subintervals with the sames rules.

The algorithm is iterative until the difference between both approximations is less that maximumError. In that case, the integral on the subinterval is approximated by the Kronrod sum.

The subdivision process is limited by maximumSubIntervals that imposes the maximum number of subintervals.

The final integral is the sum of the integrals evaluated on all the subintervals $[a_i, b_i]$ as follows:

$\int_{a}^b f(t)\di{t} = \sum_i \int_{a_i}^{b_i} f(t)\di{t}$

It is possible to get all the subintervals $[a_i, b_i]$ with a particular use of the method integrate().

Note that the integral over each subinterval $[a_i, b_i]$ uses the Gauss-Kronrod algorithm where the integrand function is rescaled by the mapping function:

(2)¶ $\varphi_i : & [-1,1] \rightarrow [a_i, b_i]\\ & x \rightarrow t = \dfrac{b_i-a_i}{2}x + \dfrac{b_i+a_i}{2}$

so that we have:

(3)¶ $\int_{a_i}^{b_i} f(t)\di{t} & = \int_{-1}^{1} \dfrac{1}{2}(b_i-a_i) f \left(\dfrac{b_i-a_i}{2}x + \dfrac{b_i+a_i}{2}\right) \di{x} \\ & = \int_{-1}^{1} \tilde{f}_i(x) \di{x}$

where we introduced the scaled function $\tilde{f}_i$ on $[-1,1]$ defined by:

$\tilde{f}_i(x) = \dfrac{1}{2}(b_i-a_i) f \circ \varphi_i (x)$

We get the nodes used to compute (1) by mapping the $2m+1$ nodes computed by GaussKronrodRule in $[-1, 1]$ according the the particular rule $G_mK_{2m+1}$ through each mapping function $\varphi_i$ defined in (2). The associated weights are multiplied by the length of the subinterval $\dfrac{1}{2}(b_i-a_i)$ .

When the function $f: \Rset^d \mapsto \Rset^p$ with $d>1$ , use the iterated quadrature algorithm of the IteratedQuadrature class.

Examples

Create a Gauss-Kronrod algorithm:

>>> import openturns as ot
>>> algo = ot.GaussKronrod(100, 1e-8, ot.GaussKronrodRule(ot.GaussKronrodRule.G11K23))

__init__(*args)¶

static GetRuleFromName(name)¶

Get the integration rule corresponding to the given name.

Parameters:

namestr: The Gauss-Kronrod rule name.

Returns:

ruleGaussKronrodRule: The rule corresponding to the given name.

static GetRules()¶

Get the collection of available integration rules.

Returns:

rulesGaussKronrodRuleCollection: Rules available for the integration.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getMaximumError()¶

Accessor to the maximal error between Gauss and Kronrod approximations.

Returns:

maximumErrorvaluefloat, positive: The maximal error between Gauss and Kronrod approximations.

getMaximumSubIntervals()¶

Accessor to the maximal number of subdivisions of $[a,b]$ .

Returns:

maximumSubIntervalsfloat, positive: The maximal number of subdivisions of the interval $[a,b]$ .

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getRule()¶

Accessor to the Gauss-Kronrod rule used in the integration algorithm.

Returns:

ruleGaussKronrodRule: The Gauss-Kronrod rule used in the integration algorithm.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

integrate(*args)¶

Evaluation of the integral of $f$ on an interval.

Available usages:

integrate(f, interval)

integrate(f, interval, error)

integrate(f, a, b, error, ai, bi, fi, ei)

Parameters:

fFunction, $f: \Rset \mapsto \Rset^p$

The integrand function.

intervalInterval, $interval \in \Rset$

The integration domain.

errorPoint

The error estimation of the approximation.

a,bfloat

Bounds of the integration interval.

ai, bi, eiPoint;

ai is the set of lower bounds of the subintervals;

bi the corresponding upper bounds;

ei the associated error estimation;

When used as input parameters, they should be empty. They are then respectively filled with the lower and upper bounds of the subintervals, and the error value.

fiSample

fi is the set of $\int_{ai}^{bi} f(t)\di{t}$

Returns:

valuePoint: Approximation of the integral.

Examples

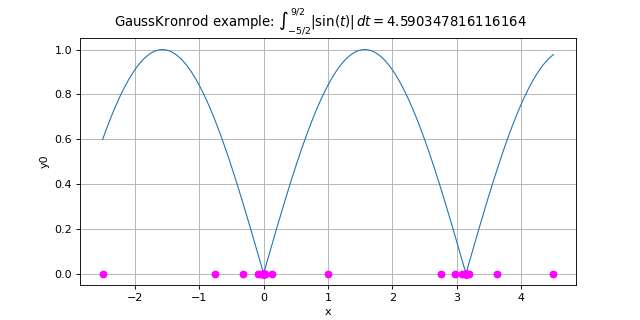
>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x'], ['abs(sin(x))'])
>>> a = -2.5
>>> b = 4.5
>>> algoGK = ot.GaussKronrod(100, 1e-8, ot.GaussKronrodRule(ot.GaussKronrodRule.G11K23))

Use the high-level usage:

>>> value = algoGK.integrate(f, ot.Interval(a, b))[0]
>>> print(value)
4.590...

Use the low-level usage:

>>> error = ot.Point()
>>> ai = ot.Point()
>>> bi = ot.Point()
>>> ei = ot.Point()
>>> fi = ot.Sample()
>>> value2 = algoGK.integrate(f, a, b, error, ai, bi, fi, ei)[0]
>>> print(value2)
4.590...

setMaximumError(maximumError)¶

Set the maximal error between Gauss and Kronrod approximations.

Parameters:

maximumErrorvaluefloat, positive: The maximal error between Gauss and Kronrod approximations.

setMaximumSubIntervals(maximumSubIntervals)¶

Set the maximal number of subdivisions of $[a,b]$ .

Parameters:

maximumSubIntervalsfloat, positive: The maximal number of subdivisions of the interval $[a,b]$ .

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setRule(rule)¶

Set the Gauss-Kronrod rule used in the integration algorithm.

Parameters:

ruleGaussKronrodRule: The Gauss-Kronrod rule used in the integration algorithm.

Examples using the class¶

Integrate a function with Gauss-Kronrod algorithm

Estimate a multivariate integral with IteratedQuadrature

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

GaussKronrod¶

Examples using the class¶