SobolIndicesExperiment¶
- class SobolIndicesExperiment(*args)¶
Experiment to computeSobol’ indices.
- Available constructors:
SobolIndicesExperiment(distribution, size, computeSecondOrder=False)
SobolIndicesExperiment(experiment, computeSecondOrder=False)
- Parameters:
- distribution
Distribution Distribution
with an independent copula used to generate the set of input data.
- sizepositive int
Size
of each of the two independent initial samples. For the total size of the experiment see notes below.
- experiment
WeightedExperiment Design of experiment used to sample the distribution.
- computeSecondOrderbool, defaults to False
Whether to add points to compute second order indices
- distribution
Methods
generate()Generate points according to the type of the experiment.
generateWithWeights(weights)Generate points and their associated weight according to the type of the experiment.
Accessor to the object's name.
Accessor to the distribution.
getName()Accessor to the object's name.
getSize()Accessor to the size of the generated sample.
Experiment accessor.
hasName()Test if the object is named.
Ask whether the experiment has uniform weights.
isRandom()Accessor to the randomness of quadrature.
setDistribution(distribution)Accessor to the distribution.
setName(name)Accessor to the object's name.
setSize(size)Accessor to the size of the generated sample.
See also
Notes
Sensitivity algorithms rely on the definition of specific designs.
The
generate()method of this class produces aSampleto be supplied to the constructor of one of theSobolIndicesAlgorithmimplementations:The chosen
SobolIndicesAlgorithmimplementation then uses the sample as input design, which means it represents (but is not a realization of) a random vector.
Either the
Distributionofor a
WeightedExperimentthat represents it must be supplied to the class constructor.If a
WeightedExperimentis supplied, the class uses it directly.If the distribution of
is supplied, the class generates a
WeightedExperiment. To do this, it duplicates the distribution: every marginal is repeated once to produce a-dimensional distribution. This trick makes it possible to choose a
WeightedExperimentwith non-iid samples (that is aLHSExperimentor aLowDiscrepancyExperiment) to represent the original-dimensional distribution.
The type of
WeightedExperimentdepends on the value of'SobolIndicesExperiment-SamplingMethod'in theResourceMap:'MonteCarlo'for aMonteCarloExperiment.'LHS'for anLHSExperimentwith alwaysShuffle and randomShift set to True.'QMC'for aLowDiscrepancyExperiment(with randomize flag set to False) built from aSobolSequence.
'MonteCarlo'is the default choice because it allows the chosenSobolIndicesAlgorithmimplementation to use the asymptotic distribution of the estimators of the Sobol’ indices.Note that
'QMC'is only possible ifSobolSequence.MaximumDimension. If'QMC'is specified butSobolSequence.MaximumDimension, the class falls back to'LHS'.>>> from openturns import SobolSequence >>> print(SobolSequence.MaximumDimension) 1111
Regardless of the type of
WeightedExperiment, the class splits it into two samples with the same size:
and
. Their columns are mixed in order to produce a very large sample: the inputDesign argument taken by one of the constructors of every
SobolIndicesAlgorithmimplementation.If computeSecondOrder is set to False, the input design is of size
. The first
rows contain the sample
and the next
rows the sample
. The last
rows contain
copies of
, each with a different column replaced by the corresponding column from
(they are the matrices
from the documentation page of
SobolIndicesAlgorithm).If computeSecondOrder is set to True and
, the input design is the same as in the case where computeSecondOrder is False (see [saltelli2002]).
If computeSecondOrder is set to True and
, the input design size is
. The first
rows are the same as when computeSecondOrder is False. The last
rows contain
copies of
, each with a different column replaced by the corresponding column from
(they are the matrices
from the documentation page of
SobolIndicesAlgorithm).Examples
Create a sample suitable to estimate first and total order Sobol’ indices:
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> formula = ['sin(pi_*X1)+7*sin(pi_*X2)^2+0.1*(pi_*X3)^4*sin(pi_*X1)'] >>> model = ot.SymbolicFunction(['X1', 'X2', 'X3'], formula) >>> distribution = ot.JointDistribution([ot.Uniform(-1.0, 1.0)] * 3) >>> size = 10 >>> experiment = ot.SobolIndicesExperiment(distribution, size) >>> sample = experiment.generate()
Create a sample suitable to estimate first, total order and second order Sobol’ indices:
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> formula = ['sin(pi_*X1)+7*sin(pi_*X2)^2+0.1*(pi_*X3)^4*sin(pi_*X1)'] >>> model = ot.SymbolicFunction(['X1', 'X2', 'X3'], formula) >>> distribution = ot.JointDistribution([ot.Uniform(-1.0, 1.0)] * 3) >>> size = 10 >>> computeSecondOrder = True >>> experiment = ot.SobolIndicesExperiment(distribution, size, computeSecondOrder) >>> sample = experiment.generate()
- __init__(*args)¶
- generate()¶
Generate points according to the type of the experiment.
- Returns:
- sample
Sample Points
of the design of experiments. The sampling method is defined by the type of the weighted experiment.
- sample
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5) >>> sample = myExperiment.generate() >>> print(sample) [ X0 X1 ] 0 : [ 0.608202 -1.26617 ] 1 : [ -0.438266 1.20548 ] 2 : [ -2.18139 0.350042 ] 3 : [ -0.355007 1.43725 ] 4 : [ 0.810668 0.793156 ]
- generateWithWeights(weights)¶
Generate points and their associated weight according to the type of the experiment.
- Returns:
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5) >>> sample, weights = myExperiment.generateWithWeights() >>> print(sample) [ X0 X1 ] 0 : [ 0.608202 -1.26617 ] 1 : [ -0.438266 1.20548 ] 2 : [ -2.18139 0.350042 ] 3 : [ -0.355007 1.43725 ] 4 : [ 0.810668 0.793156 ] >>> print(weights) [0.2,0.2,0.2,0.2,0.2]
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getDistribution()¶
Accessor to the distribution.
- Returns:
- distribution
Distribution Distribution of the input random vector.
- distribution
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getSize()¶
Accessor to the size of the generated sample.
- Returns:
- sizepositive int
Number
of points constituting the design of experiments.
- getWeightedExperiment()¶
Experiment accessor.
- Returns:
- experiment
WeightedExperiment The internal experiment.
- experiment
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- hasUniformWeights()¶
Ask whether the experiment has uniform weights.
- Returns:
- hasUniformWeightsbool
Whether the experiment has uniform weights.
- isRandom()¶
Accessor to the randomness of quadrature.
- Parameters:
- isRandombool
Is true if the design of experiments is random. Otherwise, the design of experiment is assumed to be deterministic.
- setDistribution(distribution)¶
Accessor to the distribution.
- Parameters:
- distribution
Distribution Distribution of the input random vector.
- distribution
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setSize(size)¶
Accessor to the size of the generated sample.
- Parameters:
- sizepositive int
Number
of points constituting the design of experiments.
Examples using the class¶
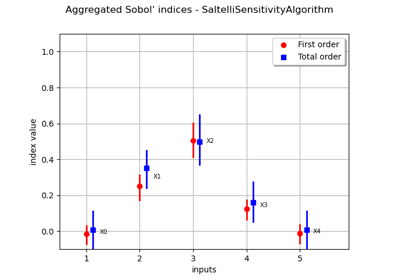
Estimate Sobol’ indices for a function with multivariate output
Example of sensitivity analyses on the wing weight model
 OpenTURNS
OpenTURNS