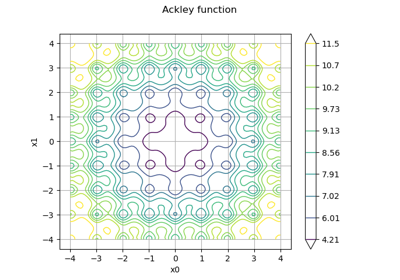
LHSExperiment¶

(Source code, png)

class LHSExperiment(*args)¶

LHS experiment.

Available constructors:

LHSExperiment(size, alwaysShuffle, randomShift)

LHSExperiment(distribution, size, alwaysShuffle, randomShift)

Parameters:

distributionDistribution: Distribution $\mu$ used to generate the set of input data.
sizepositive int: Number $\mathrm{card}\,I$ of points that will be generated in the experiment.
alwaysShufflebool: Flag to tell if the shuffle must be regenerated at each call to generate or not. Default is False: the shuffle is generated once and for all.
randomShiftbool: Flag to tell if the point selected in each cell of the shuffle is the center of the cell (randomshift is False) or if it is drawn wrt the restriction of the distribution to the cell. Default is True.

Methods

`ComputeShuffle`(dimension, totalSize)	Generate a new cell randomization for external use.
`generate`()	Generate points according to the type of the experiment.
`generateWithWeights`()	Generate points and their associated weight according to the type of the experiment.
`getAlwaysShuffle`()	Cell randomization flag accessor.
`getClassName`()	Accessor to the object's name.
`getDistribution`()	Accessor to the distribution.
`getName`()	Accessor to the object's name.
`getRandomShift`()	Randomization flag accessor.
`getShuffle`()	Return the cell randomization.
`getSize`()	Accessor to the size of the generated sample.
`hasName`()	Test if the object is named.
`hasUniformWeights`()	Ask whether the experiment has uniform weights.
`isRandom`()	Accessor to the randomness of quadrature.
`setAlwaysShuffle`(alwaysShuffle)	Cell randomization flag accessor.
`setDistribution`(distribution)	Accessor to the distribution.
`setName`(name)	Accessor to the object's name.
`setRandomShift`(randomShift)	Randomization flag accessor.
`setSize`(size)	Accessor to the size of the generated sample.

See also

WeightedExperiment

Notes

LHSExperiment is a random weighted design of experiments ([stein1987], [santner2003] page 127). The method generates a sample of points $\inputReal_i$ according to the distribution $\inputMeasure$ with the Latin Hypercube Sample (LHS) technique: some cells are determined, with the same probabilistic content according to the distribution, each line and each column contains exactly one cell, then points are selected among these selected cells. The weights associated to the points are all equal to $\frac{1}{\sampleSize}$ where $\sampleSize$ is the sample size. When recalled, the generate() method generates a new sample: the point selection within the cells changes but not the cells selection. To change the cell selection, it is necessary to create a new LHSExperiment.

Warning

When the distribution has a non-independent copula, the sample obtained by inverse isoprobabilistic transformation of an LHS experiment does not have the same properties as the original LHS experiment but can still be used to efficiently estimate threshold exceedance probabilities, especially when the copula is normal (as in this case the isoprobabilistic transformation is linear) and the limit-state is linear.

Examples

Create an LHSExperiment:

>>> import openturns as ot

Generate the sample reusing the initial shuffle and using a random shift:

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LHSExperiment(ot.Normal(2), 5, False, True)
>>> print(experiment.generate())
    [ X0        X1        ]
0 : [  0.887671 -0.647818 ]
1 : [  0.107683  1.15851  ]
2 : [  0.453077 -1.04742  ]
3 : [ -0.928012  0.409732 ]
4 : [ -0.290539  0.16153  ]
>>> print(experiment.generate())
    [ X0         X1         ]
0 : [  1.52938   -0.343515  ]
1 : [ -0.0703427  2.36353   ]
2 : [  0.576091  -1.79398   ]
3 : [ -2.11636    0.619315  ]
4 : [ -0.699601  -0.0570674 ]

Generate the sample using a new shuffle and a random shift:

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LHSExperiment(ot.Normal(2), 5, True, True)
>>> print(experiment.generate())
    [ X0        X1        ]
0 : [  0.887671 -0.647818 ]
1 : [  0.107683  1.15851  ]
2 : [  0.453077 -1.04742  ]
3 : [ -0.928012  0.409732 ]
4 : [ -0.290539  0.16153  ]
>>> print(experiment.generate())
    [ X0         X1         ]
0 : [ -1.72695   -0.591043  ]
1 : [ -0.240653  -0.0406593 ]
2 : [  0.828719   2.12547   ]
3 : [  2.37061    0.508903  ]
4 : [ -0.668296  -1.11573   ]

Generate the sample reusing the initial shuffle and using a constant shift:

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LHSExperiment(ot.Normal(2), 5, False, False)
>>> print(experiment.generate())
    [ X0        X1        ]
0 : [  1.28155  -0.524401 ]
1 : [  0         1.28155  ]
2 : [  0.524401 -1.28155  ]
3 : [ -1.28155   0.524401 ]
4 : [ -0.524401  0        ]
>>> print(experiment.generate())
    [ X0        X1        ]
0 : [  1.28155  -0.524401 ]
1 : [  0         1.28155  ]
2 : [  0.524401 -1.28155  ]
3 : [ -1.28155   0.524401 ]
4 : [ -0.524401  0        ]

Generate the sample using a new shuffle and using a constant shift:

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LHSExperiment(ot.Normal(2), 5, True, False)
>>> print(experiment.generate())
    [ X0        X1        ]
0 : [  1.28155  -0.524401 ]
1 : [  0         1.28155  ]
2 : [  0.524401 -1.28155  ]
3 : [ -1.28155   0.524401 ]
4 : [ -0.524401  0        ]
>>> print(experiment.generate())
    [ X0        X1        ]
0 : [  0.524401 -0.524401 ]
1 : [  0         1.28155  ]
2 : [ -1.28155   0        ]
3 : [ -0.524401  0.524401 ]
4 : [  1.28155  -1.28155  ]

__init__(*args)¶

static ComputeShuffle(dimension, totalSize)¶

Generate a new cell randomization for external use.

Parameters:

dimensionpositive int: Number of input dimension.
totalSizepositive int: Number $\mathrm{card}\,I$ of points that need to be shuffled.

Returns:

shuffleMatrix: For each point, the indices of the shuffled components.

generate()¶

Generate points according to the type of the experiment.

Returns:

sampleSample: Points $(\inputReal_i)_{i = 1, ..., \sampleSize}$ of the design of experiments. The sampling method is defined by the type of the weighted experiment.

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5)
>>> sample = myExperiment.generate()
>>> print(sample)
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]
3 : [ -0.355007  1.43725  ]
4 : [  0.810668  0.793156 ]

generateWithWeights()¶

Generate points and their associated weight according to the type of the experiment.

Returns:

sampleSample: The points of the design of experiments. The sampling method is defined by the nature of the experiment.
weightsPoint of size $\sampleSize$: Weights $(w_i)_{i = 1, ..., \sampleSize}$ associated with the points. By default, all the weights are equal to $\frac{1}{\sampleSize}$ .

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5)
>>> sample, weights = myExperiment.generateWithWeights()
>>> print(sample)
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]
3 : [ -0.355007  1.43725  ]
4 : [  0.810668  0.793156 ]
>>> print(weights)
[0.2,0.2,0.2,0.2,0.2]

getAlwaysShuffle()¶

Cell randomization flag accessor.

Returns:

alwaysShufflebool: Flag to tell if the shuffle must be regenerated at each call to generate or not. Default is False: the shuffle is generated once and for all.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDistribution()¶

Accessor to the distribution.

Returns:

distributionDistribution: Distribution of the input random vector.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getRandomShift()¶

Randomization flag accessor.

Returns:

randomShiftbool: Flag to tell if the point selected in each cell of the shuffle is the center of the cell (randomshift is False) or if it is drawn wrt the restriction of the distribution to the cell. Default is True.

getShuffle()¶

Return the cell randomization.

Returns:

shuffleMatrix: For each point, the indices of the shuffled components.

getSize()¶

Accessor to the size of the generated sample.

Returns:

sizepositive int: Number $\sampleSize$ of points constituting the design of experiments.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasUniformWeights()¶

Ask whether the experiment has uniform weights.

Returns:

hasUniformWeightsbool: Whether the experiment has uniform weights.

isRandom()¶

Accessor to the randomness of quadrature.

Parameters:

isRandombool: Is true if the design of experiments is random. Otherwise, the design of experiment is assumed to be deterministic.

setAlwaysShuffle(alwaysShuffle)¶

Cell randomization flag accessor.

Parameters:

alwaysShufflebool: Flag to tell if the shuffle must be regenerated at each call to generate or not. Default is False: the shuffle is generated once and for all.

setDistribution(distribution)¶

Accessor to the distribution.

Parameters:

distributionDistribution: Distribution of the input random vector.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setRandomShift(randomShift)¶

Randomization flag accessor.

Parameters:

randomShiftbool: Flag to tell if the point selected in each cell of the shuffle is the center of the cell (randomshift is False) or if it is drawn wrt the restriction of the distribution to the cell. Default is True.

setSize(size)¶

Accessor to the size of the generated sample.

Parameters:

sizepositive int: Number $\sampleSize$ of points constituting the design of experiments.

Examples using the class¶

Create a polynomial chaos metamodel by integration on the cantilever beam

Kriging: propagate uncertainties

Example of multi output Kriging on the fire satellite model

Kriging: metamodel of the Branin-Hoo function

Sequentially adding new points to a Kriging

Kriging: configure the optimization solver

Advanced Kriging

Axial stressed beam : comparing different methods to estimate a probability

Probabilistic design of experiments

Create a random design of experiments

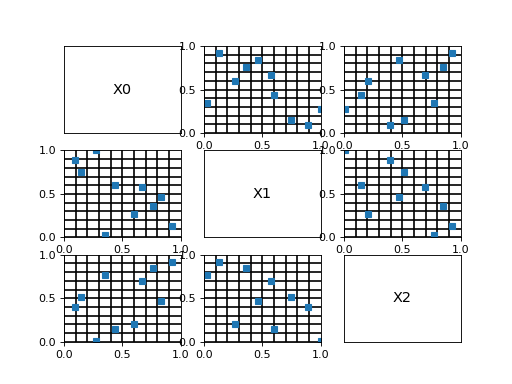
Create a design of experiments with discrete and continuous variables

Various design of experiments

Optimize an LHS design of experiments

EfficientGlobalOptimization examples

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

LHSExperiment¶

Examples using the class¶