CantileverBeam¶
- class CantileverBeam¶
Data class for the cantilever beam example.
- Attributes:
- dimint
The dimension of the problem, dim=4.
- E
Beta Young’s modulus distribution Beta(0.9, 3.5, 65.0e9, 75.0e9)
- F
LogNormal Load distribution LogNormalMuSigma()([300.0, 30.0, 0.0])
- L
Uniform Length distribution Uniform(2.5, 2.6)
- II
Beta Moment of inertia distribution Beta(2.5, 4.0, 1.3e-7, 1.7e-7)
- model
SymbolicFunction The physical model of the cantilever beam.
- R
CorrelationMatrix Correlation matrix used to define the copula.
- copula
NormalCopula Copula of the model.
- distribution
JointDistribution The joint distribution of the parameters.
- independentDistribution
JointDistribution The joint distribution of the parameters with independent copula.
Examples
>>> from openturns.usecases import cantilever_beam >>> # Load the cantilever beam model >>> cb = cantilever_beam.CantileverBeam()
- __init__()¶
Examples using the class¶
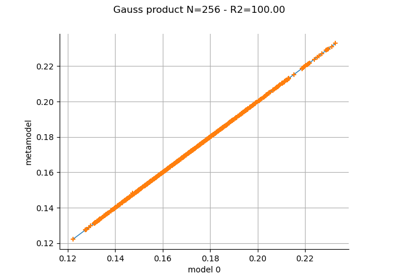
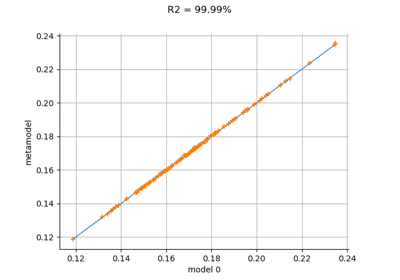
Create a polynomial chaos metamodel by integration on the cantilever beam
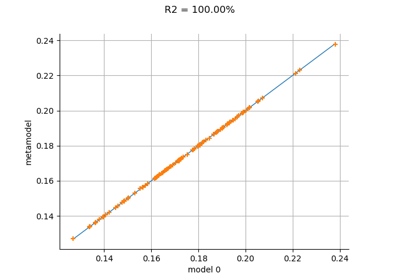
Gaussian Process Regression : cantilever beam model
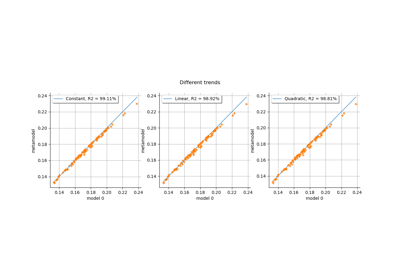
Kriging: choose a polynomial trend on the beam model

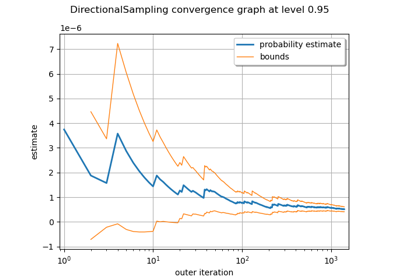
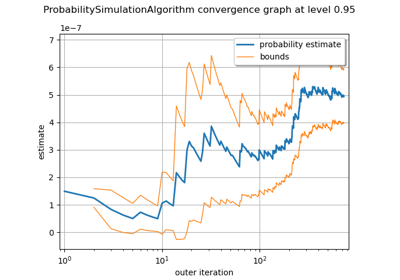
Use the Adaptive Directional Stratification Algorithm
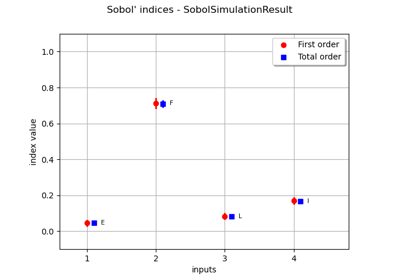
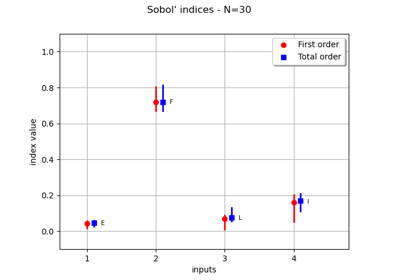
Estimate Sobol’ indices for the beam by simulation algorithm
 OpenTURNS
OpenTURNS