GaussianProcessConditionalCovariance¶
- class GaussianProcessConditionalCovariance(*args)¶
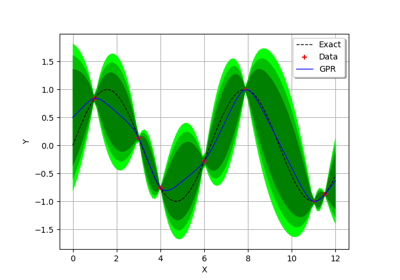
Conditional covariance post processing of a Gaussian Process Regression result.
Warning
This class is experimental and likely to be modified in future releases. To use it, import the
openturns.experimentalsubmodule.- Parameters:
- gprResult
GaussianProcessRegressionResult The result class of a Gaussian process regression.
- gprResult
Methods
Accessor to the object's name.
getConditionalCovariance(*args)Compute the conditional covariance of the Gaussian process on a point (or several points).
Compute the conditional covariance of the Gaussian process on a point (or several points).
Compute the conditional variance of the Gaussian process on a point (or several points).
getConditionalMean(*args)Compute the conditional mean of the Gaussian process on a point or a sample of points.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
Notes
The class provides services around conditional covariance of a Gaussian Process Regression
Examples
Create the model
and the samples:
>>> import openturns as ot >>> from openturns.experimental import GaussianProcessRegression >>> from openturns.experimental import GaussianProcessConditionalCovariance >>> trend = ot.SymbolicFunction(['x'], ['1']) >>> sampleX = [[1.0], [2.0], [3.0], [4.0], [5.0], [6.0]] >>> sampleY = trend(sampleX)
Create the algorithm:
>>> covarianceModel = ot.SquaredExponential([1.0]) >>> covarianceModel.setActiveParameter([])
>>> algo = GaussianProcessRegression(sampleX, sampleY, covarianceModel, trend) >>> algo.run() >>> result = algo.getResult() >>> condCov = GaussianProcessConditionalCovariance(result) >>> c = condCov([1.1])
- __init__(*args)¶
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getConditionalCovariance(*args)¶
Compute the conditional covariance of the Gaussian process on a point (or several points).
- Parameters:
- xsequence of float
The point
where the conditional covariance of the output has to be evaluated.
- sampleX2-d sequence of float
The sample
where the conditional covariance of the output has to be evaluated (M can be equal to 1).
- Returns:
- condCov
CovarianceMatrix The conditional covariance
at point
. Or the conditional covariance matrix at the sample
:
where
.
- condCov
- getConditionalMarginalCovariance(*args)¶
Compute the conditional covariance of the Gaussian process on a point (or several points).
- Parameters:
- xsequence of float
The point
where the conditional marginal covariance of the output has to be evaluated.
- sampleX2-d sequence of float
The sample
where the conditional marginal covariance of the output has to be evaluated (M can be equal to 1).
- Returns:
- condCov
CovarianceMatrix The conditional covariance
at point
.
- condCov
CovarianceMatrixCollection The collection of conditional covariance matrices
at each point of the sample
:
- condCov
Notes
In case input parameter is a of type
Sample, each element of the collection corresponds to the conditional covariance with respect to the input learning set (pointwise evaluation of the getConditionalCovariance).
- getConditionalMarginalVariance(*args)¶
Compute the conditional variance of the Gaussian process on a point (or several points).
- Parameters:
- xsequence of float
The point
where the conditional variance of the output has to be evaluated.
- sampleX2-d sequence of float
The sample
where the conditional variance of the output has to be evaluated (M can be equal to 1).
- marginalIndexint
Marginal of interest (for multiple outputs). Default value is 0
- marginalIndicessequence of int
Marginals of interest (for multiple outputs).
- Returns:
- varfloat
Variance of interest. float if one point (x) and one marginal of interest (x, marginalIndex)
- varPointsequence of float
The marginal variances
Notes
In case of fourth usage, the sequence of float is given as the concatenation of marginal variances for each point in sampleX.
- getConditionalMean(*args)¶
Compute the conditional mean of the Gaussian process on a point or a sample of points.
- Parameters:
- xsequence of float
The point
where the conditional mean of the output has to be evaluated.
- sampleX2-d sequence of float
The sample
where the conditional mean of the output has to be evaluated (M can be equal to 1).
- Returns:
- condMean
Point The conditional mean
at point
. Or the conditional mean matrix at the sample
:
- condMean
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
 OpenTURNS
OpenTURNS