VisualTest_DrawHenryLine

(Source code, png, hires.png, pdf)

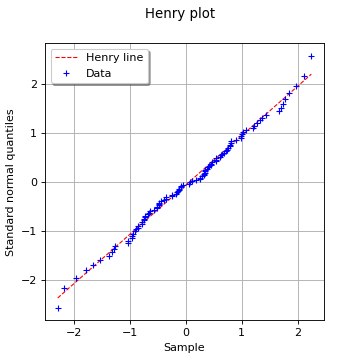
../../_images/VisualTest_DrawHenryLine.png
VisualTest_DrawHenryLine(\*args)

Draw an Henry plot.

Refer to Graphical goodness-of-fit tests.

Parameters
sample2-d sequence of float

Tested (univariate) sample.

normal_distributionNormal, optional

Tested (univariate) normal distribution.

If not given, this will build a Normal distribution from the given sample using the NormalFactory.

Returns
graphGraph

The graph object

See also

VisualTest_DrawQQplot, FittingTest_Kolmogorov

Notes

The Henry plot is a visual fitting test for the normal distribution. It opposes the sample quantiles to those of the standard normal distribution (the one with zero mean and unit variance) by plotting the following points could:

\left(x^{(i)}, \Phi^{-1}\left(\widehat{F}\left(x^{(i)}\right)\right) \right), \quad i = 1, \ldots, m

where \widehat{F} denotes the empirical CDF of the sample and \Phi^{-1} denotes the quantile function of the standard normal distribution.

If the given sample fits to the tested normal distribution (with mean \mu and standard deviation \sigma), then the points should be close to be aligned (up to the uncertainty associated with the estimation of the empirical probabilities) on the Henry line whose equation reads:

y = \frac{x - \mu}{\sigma}, \quad x \in \Rset

The Henry plot is a special case of the more general QQ-plot.

Examples

>>> import openturns as ot
>>> from openturns.viewer import View

Generate a random sample from a Normal distribution:

>>> ot.RandomGenerator.SetSeed(0)
>>> distribution = ot.Normal(2.0, 0.5)
>>> sample = distribution.getSample(30)

Draw an Henry plot against a given (wrong) Normal distribution:

>>> henry_graph = ot.VisualTest.DrawHenryLine(sample, distribution)
>>> henry_graph.setTitle('Henry plot against given %s' % ot.Normal(3.0, 1.0))
>>> View(henry_graph).show()

Draw an Henry plot against an inferred Normal distribution:

>>> henry_graph = ot.VisualTest.DrawHenryLine(sample)
>>> henry_graph.setTitle('Henry plot against inferred Normal distribution')
>>> View(henry_graph).show()