A simple stressed beam¶
We consider a simple beam stressed by a traction load F at both sides.

Beam geometry¶
The geometry is supposed to be deterministic; the diameter D is equal to:
By definition, the yield stress is the load divided by the surface. Since the surface is , the stress is:
Failure occurs when the beam plastifies, i.e. when the axial stress gets larger than the yield stress:
where is the strength.
Therefore, the limit state function is:
for any .
The value of the parameter is such that:
which leads to the equation:
We consider the following distribution functions.
Variable |
Distribution |
|---|---|
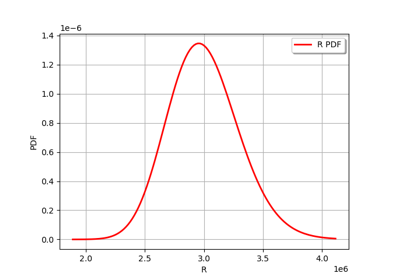
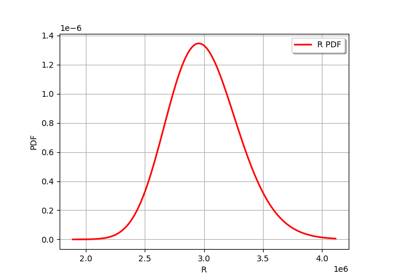
R |
LogNormal( |
F |
Normal( |
where
and
are the mean and the variance of
.
The failure probability is:
The exact is
Load the use case¶
We can load this classical model from the use cases module as follows :
>>> from openturns.usecases import stressed_beam as stressed_beam
>>> # Load the use case axial stressed beam
>>> sb = stressed_beam.AxialStressedBeam()
API documentation¶
See AxialStressedBeam.
 OpenTURNS
OpenTURNS