A flood model

Introduction

The following figure presents a dyke protecting industrial facilities. When the river level exceeds the dyke height, flooding occurs. The model is based on a crude simplification of the 1D hydrodynamical equations of Saint-Venant under the assumptions of uniform and constant flow rate and large rectangular sections.

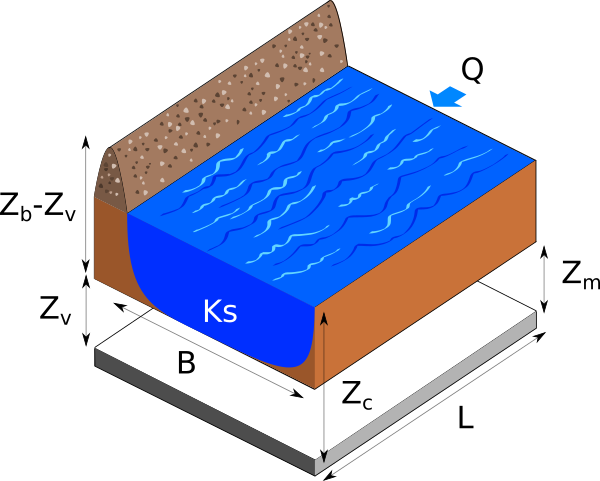
flooding section

Flooding section

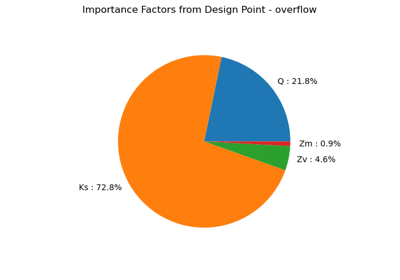
Four independent random variables are considered:

  • Q: flow rate [m^3 s^{-1}]

  • K_s: Strickler [m^{1/3} s^{-1}]

  • Z_v: downstream height [m]

  • Z_m: upstream height [m]

When the Strickler coefficient increases, the riverbed generates less friction.

The model depends on four parameters:

  • the height of the dyke: H_d = 3 [m],

  • the altitude of the river banks: Z_b = 55.5 [m],

  • the river length: L = 5000 [m],

  • the river width: B = 300 [m].

The altitude of the dyke is:

Z_d = Z_b + H_d

The slope \alpha of the river is assumed to be close to zero, which implies:

\alpha = \frac{Z_m - Z_v}{L},

if Z_m \geq Z_v.

The water depth is:

H = \left(\frac{Q}{K_s B \sqrt{\alpha}}\right)^{0.6},

for any K_s, Q>0.

The flood altitude is:

Z_c = H + Z_v.

The altitude of the surface of the water is greater than the altitude of the top of the dyke (i.e. there is a flood) if:

S = Z_c - Z_d

is greater than zero.

The following figure presents the model with more details.

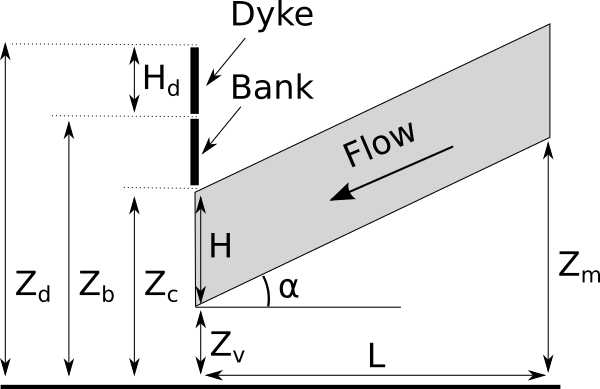
flooding section details

Flooding section detail

If we substitute the parameters into the equation, we get:

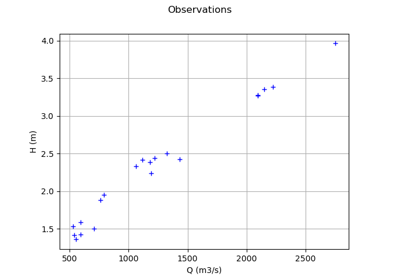
S = \left(\frac{Q}{300 Ks \sqrt{(Zm-Zv)/5000}}\right)^{3/5} +Zv-58.5.

We assume that the four inputs have the following distributions:

  • Q ~ Gumbel(mode=1013, scale=558), Q > 0

  • K_s ~ Normal(mu=30.0, sigma=7.5), K_s > 0

  • Z_v ~ Uniform(a=49, b=51)

  • Z_m ~ Uniform(a=54, b=56)

Moreover, we assume that the input random variables are independent.

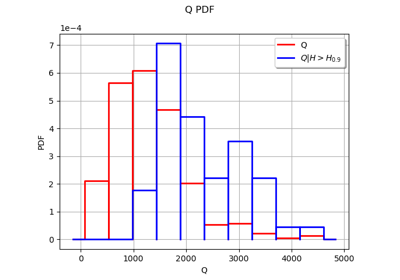
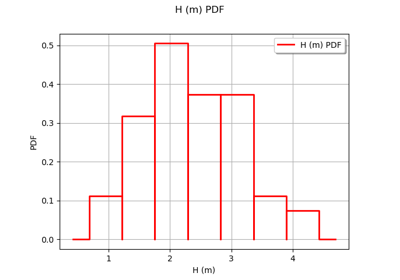
We want to estimate the flood probability:

P_f = P(S>0).

References

  • Iooss B, Lemaître P (2015) A review on global sensitivity analysis methods. In: Meloni C., Dellino G. (eds) Uncertainty management in Simulation-Optimization of Complex Systems: Algorithmsand Applications, Springer

  • Baudin M., Dutfoy A., Iooss B., Popelin AL. (2015) OpenTURNS: An Industrial Software for Uncertainty Quantification in Simulation. In: Ghanem R., Higdon D., Owhadi H. (eds) Handbook of Uncertainty Quantification. Springer

Load the use case

We can load this classical model from the use cases module as follows :

>>> from openturns.usecases import flood_model as flood_model
>>> # Load the use case flood model
>>> fm = flood_model.FloodModel()

API documentation

See FloodModel.