Note

Click here to download the full example code

Gibbs sampling of the posterior distribution¶

We sample the from the posterior distribution of the parameters of a mixture model.

$X \sim 0.7 \mathcal{N}(\mu_0, 1) + 0.3 \mathcal{N}(\mu_1, 1),$

where $\mu_0$ and $\mu_1$ are unknown parameters. They are a priori i.i.d. with prior distribution $\mathcal{N}(0, \sqrt{10})$ . This example is drawn from Example 9.2 from Monte-Carlo Statistical methods by Robert and Casella (2004).

import openturns as ot
from openturns.viewer import View
import numpy as np

ot.RandomGenerator.SetSeed(100)

Sample data with $\mu_0 = 0$ and $\mu_1 = 2.7$ .

N = 500
p = 0.3

mu0 = 0.0
mu1 = 2.7
nor0 = ot.Normal(mu0, 1.0)
nor1 = ot.Normal(mu1, 1.0)
true_distribution = ot.Mixture([nor0, nor1], [1 - p, p])
observations = np.array(true_distribution.getSample(500))

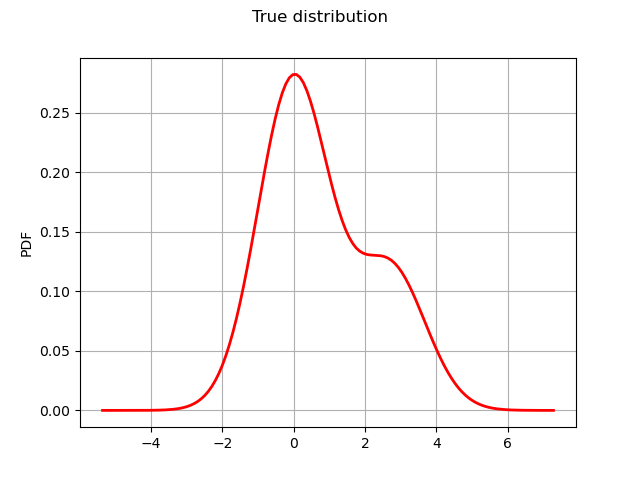
Plot the true distribution.

graph = true_distribution.drawPDF()
graph.setTitle("True distribution")
graph.setXTitle("")
graph.setLegends([""])
View(graph)

Out:

<openturns.viewer.View object at 0x7f7308fad0c0>

A natural step at this point is to introduce an auxiliary (unobserved) random variable $Z$ telling from which distribution $X$ was sampled.

For any nonnegative integer $i$ , $Z_i$ follows the Bernoulli distribution with $p=0.3$ , and $X_i | Z_i \sim \mathcal{N}(\mu_{Z_i}, 1.0)$ .

Let $n_0$ (resp. $n_1$ ) denote the number of indices $i$ such that $Z_i=0$ (resp. $Z_i=1$ ).

Conditionally to all $X_i$ and all $Z_i$ , $\mu_0$ and $\mu_1$ are independent: $\mu_0$ follows $\mathcal{N} \left(\sum_{Z_i=0} \frac{X_i}{0.1 + n_0}, \frac{1}{0.1 + n_0} \right)$ and $\mu_1$ follows $\mathcal{N} \left(\sum_{Z_i=1} \frac{X_i}{0.1 + n_1}, \frac{1}{0.1 + n_1} \right)$ .

For any $i$ , conditionally to $X_i$ , $\mu_0$ and $\mu_1$ , $Z_i$ is independent from all $Z_j$ ( $j \neq i$ ) and follows the Bernoulli distribution with parameter

$p = \frac{p \exp \left( -(X_i - \mu_1)^2 / 2 \right) }{p \exp \left( -(X_i - \mu_1)^2 / 2 \right) + (1-p) \exp \left( -(X_i - \mu_0)^2 / 2 \right) }$

We now sample from the joint distribution of $(\mu_0, \mu1, Z_0,...,Z_{N-1})$ conditionally to the $X_i$ using the Gibbs algorithm. We define functions that will translate a given state of the Gibbs algorithm into the correct parameters for the distributions of $\mu_0$ , $\mu_1$ , and the $Z_i$ .

def nor0post(pt):
    z = np.array(pt)[2:]
    x0 = observations[z == 0]
    mu0 = x0.sum() / (0.1 + len(x0))
    sigma0 = 1.0 / (0.1 + len(x0))
    return [mu0, sigma0]


def nor1post(pt):
    z = np.array(pt)[2:]
    x1 = observations[z == 1]
    mu1 = x1.sum() / (0.1 + len(x1))
    sigma1 = 1.0 / (0.1 + len(x1))
    return [mu1, sigma1]


def zpost(pt):
    mu0 = pt[0]
    mu1 = pt[1]
    term1 = p * np.exp(- (observations - mu1)**2 / 2)
    term0 = (1.0 - p) * np.exp(- (observations - mu0)**2 / 2)
    res = term1 / (term1 + term0)
    # output must be a 1d list or array in order to create a PythonFunction
    return res.reshape(-1)


nor0posterior = ot.PythonFunction(2 + N, 2, nor0post)
nor1posterior = ot.PythonFunction(2 + N, 2, nor1post)
zposterior = ot.PythonFunction(2 + N, N, zpost)

We can now construct the Gibbs algorithm

initialState = [0.0] * (N + 2)

sampler0 = ot.RandomVectorMetropolisHastings(
    ot.RandomVector(ot.Normal()), initialState, [0], nor0posterior)
sampler1 = ot.RandomVectorMetropolisHastings(
    ot.RandomVector(ot.Normal()), initialState, [1], nor1posterior)

big_bernoulli = ot.ComposedDistribution([ot.Bernoulli()] * N)

sampler2 = ot.RandomVectorMetropolisHastings(ot.RandomVector(
    big_bernoulli), initialState, range(2, N + 2), zposterior)

gibbs = ot.Gibbs([sampler0, sampler1, sampler2])

Run the Gibbs algorithm

s = gibbs.getSample(10000)

Extract the relevant marginals: the first ( $mu_0$ ) and the second ( $\mu_1$ ).

posterior_sample = s[:, 0:2]

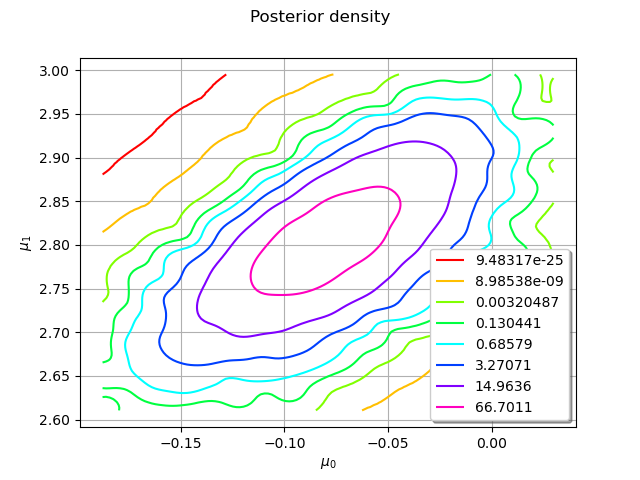
Let us plot the posterior density.

ks = ot.KernelSmoothing().build(posterior_sample)
graph = ks.drawPDF()
graph.setTitle("Posterior density")
graph.setLegendPosition("bottomright")
graph.setXTitle(r"$\mu_0$")
graph.setYTitle(r"$\mu_1$")
View(graph)

View.ShowAll()

Total running time of the script: ( 0 minutes 14.314 seconds)

Gallery generated by Sphinx-Gallery

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

Gibbs sampling of the posterior distribution¶