Create a normal process

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

Create a gaussian process from a covariance model

In this paragraph we build a gaussian process from its covariance model.

We first define a covariance model :

defaultDimension = 1
# Amplitude values
amplitude = [1.0]*defaultDimension
# Scale values
scale = [1.0]*defaultDimension
# Covariance model
myModel = ot.AbsoluteExponential(scale, amplitude)

We define a mesh,

tmin = 0.0
step = 0.1
n = 11
myTimeGrid = ot.RegularGrid(tmin, step, n)

and create the process :

process = ot.GaussianProcess(myModel, myTimeGrid)
print(process)

Out:

GaussianProcess(trend=[x0]->[0.0], covariance=AbsoluteExponential(scale=[1], amplitude=[1]))

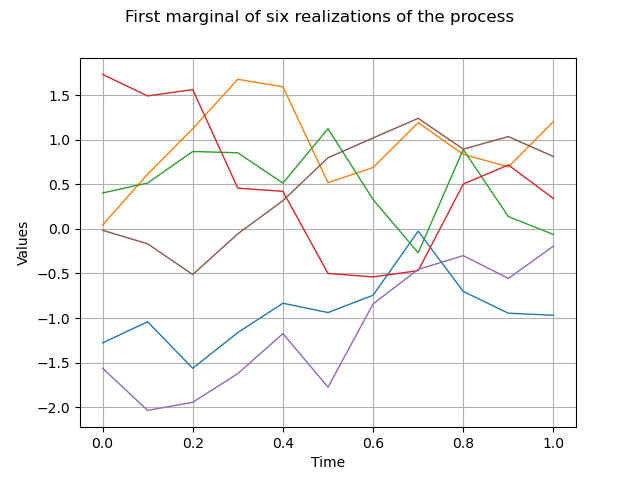
We draw the first marginal of a sample of size 6 :

sample = process.getSample(6)
graph = sample.drawMarginal(0)
graph.setTitle("First marginal of six realizations of the process")
view = viewer.View(graph)

Create a gaussian process from spectral density

In this paragraph we build a gaussian process from its spectral density.

We first define a spectral model :

amplitude = [1.0, 2.0]
scale = [4.0, 5.0]
spatialCorrelation = ot.CorrelationMatrix(2)
spatialCorrelation[0, 1] = 0.8
mySpectralModel = ot.CauchyModel(scale, amplitude, spatialCorrelation)

As usual we define a mesh,

myTimeGrid = ot.RegularGrid(0.0, 0.1, 20)

and create the process thereafter

process = ot.SpectralGaussianProcess(mySpectralModel, myTimeGrid)
print(process)

Out:

 SpectralGaussianProcess=SpectralGaussianProcess dimension=2 spectralModel=class=CauchyModel amplitude=[1,2] scale=[4,5] spatial correlation=
[[ 1   0.8 ]
 [ 0.8 1   ]] maximal frequency=5 n frequency=10

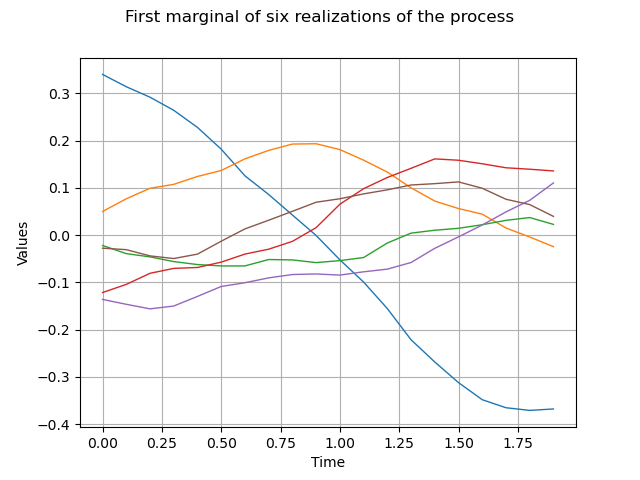
Eventually we draw the first marginal of a sample of size 6 :

sample = process.getSample(6)
graph = sample.drawMarginal(0)
graph.setTitle("First marginal of six realizations of the process")
view = viewer.View(graph)

Display figures

plt.show()