Use the Importance Sampling algorithm

In this example we estimate a failure probability with the importance sampling simulation algorithm provided by the ImportanceSamplingExperiment class.

The main steps of this method are:

• run a FORM analysis,

• create an importance distribution based on the results of the FORM results,

• run a sampling-based probability estimate algorithm.

We shall consider the analytical example of a cantilever beam.

Define the cantilever beam model

from openturns.usecases import cantilever_beam
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

The cantilever beam example can be accessed in the usecases module :

cb = cantilever_beam.CantileverBeam()

The joint probability distribution of the input parameters is stored in the object cb :

distribution = cb.distribution

We create the model.

model = cb.model

Define the event

We create the event whose probability we want to estimate.

vect = ot.RandomVector(distribution)
G = ot.CompositeRandomVector(model, vect)
event = ot.ThresholdEvent(G, ot.Greater(), 0.30)

Run a FORM analysis

Define a solver

optimAlgo = ot.Cobyla()
optimAlgo.setMaximumEvaluationNumber(1000)
optimAlgo.setMaximumAbsoluteError(1.0e-10)
optimAlgo.setMaximumRelativeError(1.0e-10)
optimAlgo.setMaximumResidualError(1.0e-10)
optimAlgo.setMaximumConstraintError(1.0e-10)

Run FORM

algo = ot.FORM(optimAlgo, event, distribution.getMean())
algo.run()
result = algo.getResult()

Configure an importance sampling algorithm

The getStandardSpaceDesignPoint method returns the design point in the U-space.

standardSpaceDesignPoint = result.getStandardSpaceDesignPoint()
standardSpaceDesignPoint

[-0.665643,4.31264,1.23029,-1.3689]

The key point is to define the importance distribution in the U-space. To define it, we use a multivariate standard Gaussian centered around the design point in the U-space.

dimension = distribution.getDimension()
dimension

Out:

4

myImportance = ot.Normal(dimension)
myImportance.setMean(standardSpaceDesignPoint)
myImportance

Normal(mu = [-0.665643,4.31264,1.23029,-1.3689], sigma = [1,1,1,1], R = [[ 1 0 0 0 ]
[ 0 1 0 0 ]
[ 0 0 1 0 ]
[ 0 0 0 1 ]])

Create the design of experiment corresponding to importance sampling. This generates a WeightedExperiment with weights fitting to the importance distribution.

experiment = ot.ImportanceSamplingExperiment(myImportance)
type(experiment)

Create the standard event corresponding to the event. This pushes the original problem to the U-space, with Gaussian independent marginals.

standardEvent = ot.StandardEvent(event)

Run the importance sampling simulation

We then create the simulation algorithm.

algo = ot.ProbabilitySimulationAlgorithm(standardEvent, experiment)
algo.setMaximumCoefficientOfVariation(0.1)
algo.setMaximumOuterSampling(40000)
algo.run()

We can retrieve results of this estimate :

result = algo.getResult()
probability = result.getProbabilityEstimate()
print("Probability = ", probability)

Out:

Probability =  3.9776311366448274e-07

In order to compute the confidence interval, we use the getConfidenceLength method, which returns the length of the interval. In order to compute the bounds of the interval, we divide this length by 2.

alpha = 0.05

pflen = result.getConfidenceLength(1-alpha)
print("%.2f%% confidence interval = [%.10f,%.10f]" % (
    (1-alpha)*100, probability-pflen/2, probability+pflen/2))

Out:

95.00% confidence interval = [0.0000003198,0.0000004757]

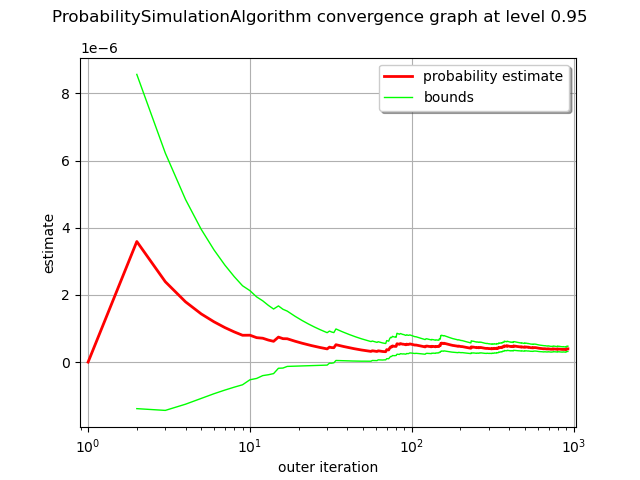
We can observe the convergence history of the estimate with the drawProbabilityConvergence method which displays the estimate and confidence interval evolution.

graph = algo.drawProbabilityConvergence()
graph.setLogScale(ot.GraphImplementation.LOGX)
view = viewer.View(graph)