Linear regression

This method deals with the parametric modelling of a probability distribution for a random vector \vect{X} = \left( X^1,\ldots,X^{n_X} \right). It aims to measure a type of dependence (here a linear relation) which may exist between a component X^i and other uncertain variables X^j.

The principle of the multiple linear regression model is to find the function that links the variable X^i to other variables X^{j_1},…,X^{j_K} by means of a linear model:

\begin{aligned} X^i = a_0 + \sum_{j \in \{ j_1,\ldots,j_K \} } a_j X^j + \varepsilon \end{aligned}

where \varepsilon describes a random variable with zero mean and standard deviation \sigma independent of the input variables X^i. For given values of X^{j_1},…,X^{j_K}, the average forecast of X^i is denoted by \widehat{X}^i and is defined as:

\begin{aligned} \widehat{X}^i = a_0 + \sum_{j \in \{ j_1,\ldots,j_K \} } a_j X^j \end{aligned}

The estimators for the regression coefficients \widehat{a}_0,\widehat{a}_1,\ldots,\widehat{a}_{K}, and the standard deviation \sigma are obtained from a sample of (X^i,X^{j_1},\ldots,X^{j_K}), that is a set of N values (x^i_1,x_1^{j_1},\ldots,x_1^{j_K}),…,(x^i_n,x_n^{j_1},\ldots,x_n^{j_K}). They are determined via the least-squares method:

\begin{aligned} \left\{ \widehat{a}_0,\widehat{a}_1,\ldots,\widehat{a}_{K} \right\} = \textrm{argmin} \sum_{k=1}^n \left[ x^i_k - a_0 - \sum_{j \in \{ j_1,\ldots,j_K \} } a_j x^j_k \right]^2 \end{aligned}

In other words, the principle is to minimize the total quadratic distance between the observations x^i_k and the linear forecast \widehat{x}^i_k.

Some estimated coefficient \widehat{a}_\ell may be close to zero, which may indicate that the variable X^{j_\ell} does not bring valuable information to forecast X^i. A classical statistical test to identify such situations is available: Fisher’s test. For each estimated coefficient \widehat{a}_\ell, an important characteristic is the so-called “p-value” of Fisher’s test. The coefficient is said to be “significant” if and only if \alpha_{\ell \textrm{lim}} is greater than a value \alpha chosen by the user (typically 5% or 10%). The higher the p-value, the more significant the coefficient.

Another important characteristic of the adjusted linear model is the coefficient of determination R^2. This quantity indicates the part of the variance of X^i that is explained by the linear model:

\begin{aligned} R^2 = \frac{ \displaystyle \sum_{k=1}^n \left( x^i_k - \overline{x}^i \right)^2 - \sum_{k=1}^n \left( x^i_k - \widehat{x}_k^i \right)^2 }{ \sum_{k=1}^n \left( x^i_k - \overline{x}^i \right)^2 } \end{aligned}

where \overline{x}^i denotes the empirical mean of the sample \left\{ x^i_1,\ldots,x^i_n \right\}.

Thus, 0 \leq R^2 \leq 1. A value close to 1 indicates a good fit of the linear model, whereas a value close to 0 indicates that the linear model does not provide a relevant forecast. A statistical test allows one to detect significant values of R^2. Again, a p-value is provided: the higher the p-value, the more significant the coefficient of determination.

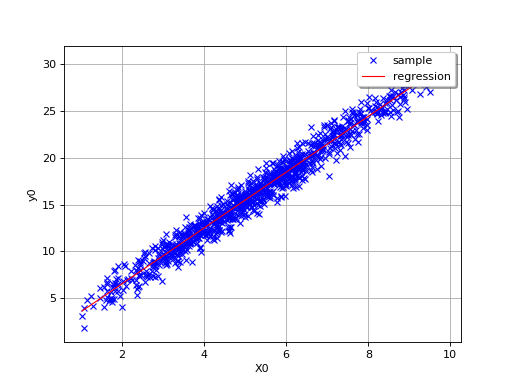
By definition, the multiple regression model is only relevant for linear relationships, as in the following simple example where X^2 = a_0 + a_1 X^1.

(Source code, png, hires.png, pdf)

../../_images/linear_regression-1.png

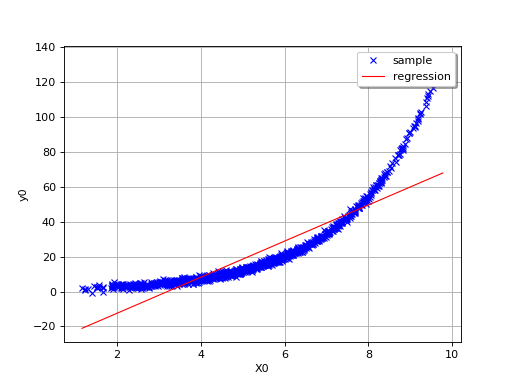
In this second example (still in dimension 1), the linear model is not relevant because of the exponential shape of the relation. But a linear approach would be useful on the transformed problem X^2 = a_0 + a_1 \exp X^1. In other words, what is important is that the relationships between X^i and the variables X^{j_1},…,X^{j_K} is linear with respect to the regression coefficients a_j.

(Source code, png, hires.png, pdf)

../../_images/linear_regression-2.png

The value of R^2 is a good indication of the goodness-of fit of the linear model. However, several other verifications have to be carried out before concluding that the linear model is satisfactory. For instance, one has to pay attentions to the “residuals” \{ u_1,\ldots,u_N \} of the regression:

\begin{aligned} u_j = x^i - \widehat{x}^i \end{aligned}

A residual is thus equal to the difference between the observed value of X^i and the average forecast provided by the linear model. A key-assumption for the robustness of the model is that the characteristics of the residuals do not depend on the value of X^i,X^{j_1},\dots,X^{j_K}: the mean value should be close to 0 and the standard deviation should be constant. Thus, plotting the residuals versus these variables can fruitful.

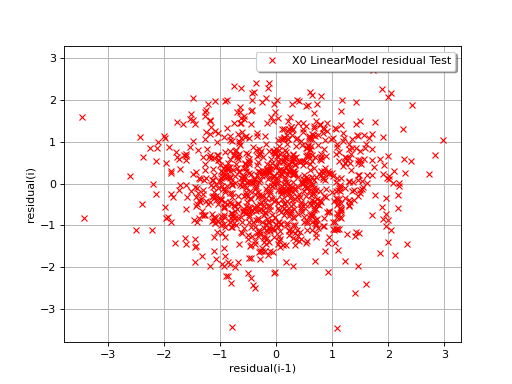
In the following example, the behavior of the residuals is satisfactory: no particular trend can be detected neither in the mean nor in he standard deviation.

(Source code, png, hires.png, pdf)

../../_images/linear_regression-3.png

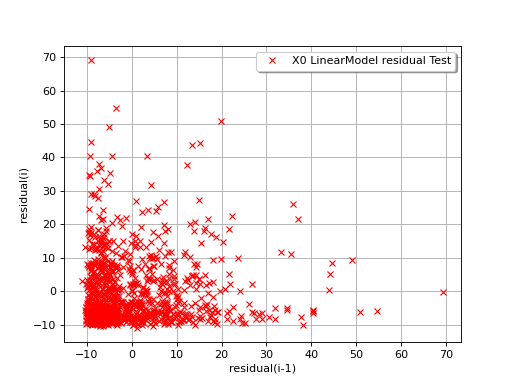
The next example illustrates a less favorable situation: the mean value of the residuals seems to be close to 0 but the standard deviation tends to increase with X. In such a situation, the linear model should be abandoned, or at least used very cautiously.

(Source code, png, hires.png, pdf)

../../_images/linear_regression-4.png

API:

  • See LinearModelAlgorithm to build a linear model

  • See LinearModelResult for the associated results

  • See VisualTest_DrawLinearModel() to draw a linear model

  • See VisualTest_DrawLinearModelResidual() to draw the residual

  • See LinearModelTest_LinearModelFisher() to assess the nullity of the coefficients

  • See LinearModelTest_LinearModelResidualMean() to assess the mean residual

  • See LinearModelTest_LinearModelHarrisonMcCabe() to assess the homoscedasticity of the residual

  • See LinearModelTest_LinearModelBreuschPagan() to assess the homoscedasticity of the residual

  • See LinearModelTest_LinearModelDurbinWatson() to assess the autocorrelation of the residual

Examples:

References: