Spearman correlation coefficient¶

This method deals with the parametric modelling of a probability distribution for a random vector $\vect{X} = \left( X^1,\ldots,X^{n_X} \right)$ . It aims to measure a type of dependence (here a monotonous correlation) which may exist between two components $X^i$ and $X^j$ .

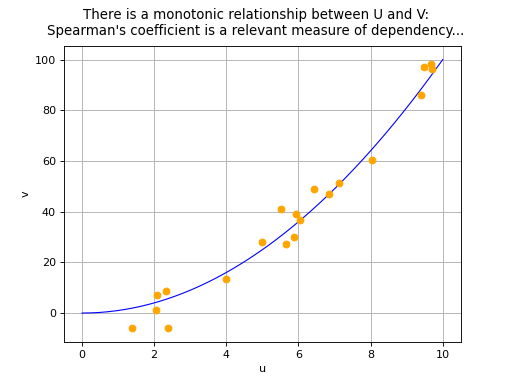
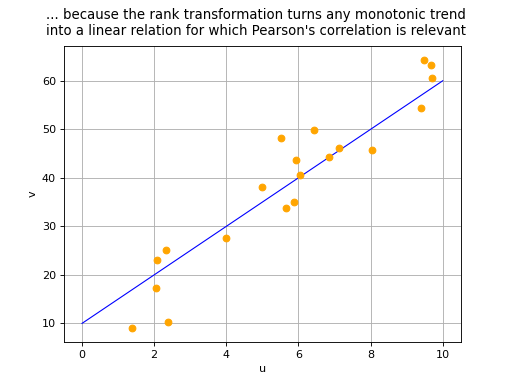
The Spearman’s correlation coefficient $\rho^S_{U,V}$ aims to measure the strength of a monotonic relationship between two random variables $U$ and $V$ . It is in fact equivalent to the Pearson’s correlation coefficient after having transformed $U$ and $V$ to linearize any monotonic relationship (remember that Pearson’s correlation coefficient may only be used to measure the strength of linear relationships, see Pearson’s correlation coefficient):

$\begin{aligned} \rho^S_{U,V} = \rho_{F_U(U),F_V(V)} \end{aligned}$

where $F_U$ and $F_V$ denote the cumulative distribution functions of $U$ and $V$ .

If we arrange a sample made up of $N$ pairs $\left\{ (u_1,v_1),(u_2,v_2),\ldots,(u_N,v_N) \right\}$ , the estimation of Spearman’s correlation coefficient first of all requires a ranking to produce two samples $(u_1,\ldots,u_N)$ and $(v_1,\ldots,v_N)$ . The ranking $u_{[i]}$ of the observation $u_i$ is defined as the position of $u_i$ in the sample reordered in ascending order: if $u_i$ is the smallest value in the sample $(u_1,\ldots,u_N)$ , its ranking would equal 1; if $u_i$ is the second smallest value in the sample, its ranking would equal 2, and so forth. The ranking transformation is a procedure that takes the sample $(u_1,\ldots,u_N)$ ) as input data and produces the sample $(u_{[1]},\ldots,u_{[N]})$ as an output result.

For example, let us consider the sample $(u_1,u_2,u_3,u_4) = (1.5,0.7,5.1,4.3)$ . We therefore have $(u_{[1]},u_{[2]}u_{[3]},u_{[4]}) = (2,1,4,3)$ . $u_1 = 1.5$ is in fact the second smallest value in the original, $u_2 = 0.7$ the smallest, etc.

The estimation of Spearman’s correlation coefficient is therefore equal to Pearson’s coefficient estimated with the aid of the $N$ pairs $(u_{[1]},v_{[1]})$ , $(u_{[2]},v_{[2]})$ , …, $(u_{[N]},v_{[N]})$ :

$\begin{aligned} \widehat{\rho}^S_{U,V} = \frac{ \displaystyle \sum_{i=1}^N \left( u_{[i]} - \overline{u}_{[]} \right) \left( v_{[i]} - \overline{v}_{[]} \right) }{ \sqrt{\displaystyle \sum_{i=1}^N \left( u_{[i]} - \overline{u}_{[]} \right)^2 \left( v_{[i]} - \overline{v}_{[]} \right)^2} } \end{aligned}$

where $\overline{u}_{[]}$ and $\overline{v}_{[]}$ represent the empirical means of the samples $(u_{[1]},\ldots,u_{[N]})$ and $(v_{[1]},\ldots,v_{[N]})$ .

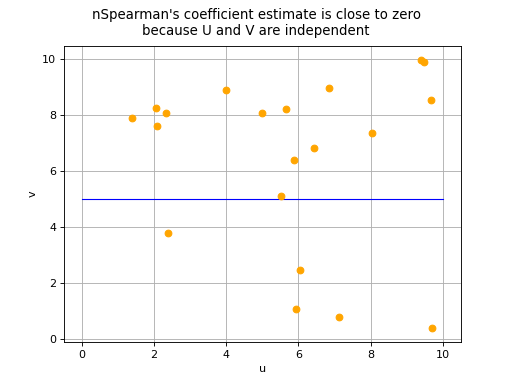
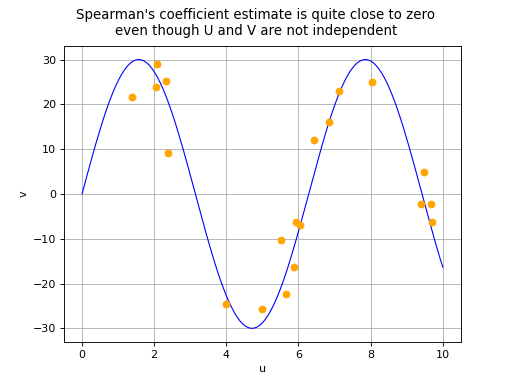
The Spearman’s correlation coefficient takes values between -1 and 1. The closer its absolute value is to 1, the stronger the indication is that a monotonic relationship exists between variables $U$ and $V$ . The sign of Spearman’s coefficient indicates if the two variables increase or decrease in the same direction (positive coefficient) or in opposite directions (negative coefficient). We note that a correlation coefficient equal to 0 does not necessarily imply the independence of variables $U$ and $V$ . There are two possible situations in the event of a zero Spearman’s correlation coefficient: