SORMResult¶

class SORMResult(*args)¶

Result of a SORM analysis.

Available constructors:: SORMResult(designPoint, limitStateVariable, isInFailureSpace)

Parameters:

designPointsequence of float: Design point in the standard space resulting from the optimization algorithm.
limitStateVariableRandomVector: Event of which the probability is calculated.
isInFailureSpacebool: Indicates whether the origin of the standard space is in the failure space.

See also

Analytical, AnalyticalResult, FORM, FORMResult, StrongMaximumTest

Notes

Structure created by the method run() of the SORM class and obtained thanks to its method getResult().

Methods

`drawHasoferReliabilityIndexSensitivity`(*args)	Draw the sensitivity of the Hasofer Reliability Index.
`drawImportanceFactors`(*args)	Draw the importance factors.
`getClassName`()	Accessor to the object's name.
`getEventProbabilityBreitung`()	Accessor to the failure probability $P_{Breitung}$ .
`getEventProbabilityHohenbichler`()	Accessor to the failure probability $P_{Hohenbichler}$ .
`getEventProbabilityTvedt`()	Accessor to the failure probability $P_{Tvedt}$ .
`getGeneralisedReliabilityIndexBreitung`()	Accessor to the Generalised Reliability Index Breitung.
`getGeneralisedReliabilityIndexHohenbichler`()	Accessor to the Generalised Reliability Index Hohenbichler.
`getGeneralisedReliabilityIndexTvedt`()	Accessor to the Generalised Reliability Index Tvedt.
`getHasoferReliabilityIndex`()	Accessor to the Hasofer Reliability Index.
`getHasoferReliabilityIndexSensitivity`()	Accessor to the sensitivities of the Hasofer Reliability Index.
`getId`()	Accessor to the object's id.
`getImportanceFactors`(*args)	Accessor to the importance factors.
`getIsStandardPointOriginInFailureSpace`()	Accessor to know if the standard point origin is in the failure space.
`getLimitStateVariable`()	Accessor to the event of which the probability is calculated.
`getMeanPointInStandardEventDomain`()	Accessor to the mean point in the standard event domain.
`getName`()	Accessor to the object's name.
`getOptimizationResult`()	Accessor to the result of the optimization problem.
`getPhysicalSpaceDesignPoint`()	Accessor to the design point in the physical space.
`getShadowedId`()	Accessor to the object's shadowed id.
`getSortedCurvatures`()	Accessor to the sorted curvatures.
`getStandardSpaceDesignPoint`()	Accessor to the design point in the standard space.
`getVisibility`()	Accessor to the object's visibility state.
`hasName`()	Test if the object is named.
`hasVisibleName`()	Test if the object has a distinguishable name.
`setIsStandardPointOriginInFailureSpace`(...)	Accessor to specify if the standard point origin is in the failure space.
`setMeanPointInStandardEventDomain`(...)	Accessor to the mean point in the standard event domain.
`setName`(name)	Accessor to the object's name.
`setOptimizationResult`(optimizationResult)	Accessor to the result of the optimization problem.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setStandardSpaceDesignPoint`(...)	Accessor to the design point in the standard space.
`setVisibility`(visible)	Accessor to the object's visibility state.

__init__(*args)¶

drawHasoferReliabilityIndexSensitivity(*args)¶

Draw the sensitivity of the Hasofer Reliability Index.

Parameters:

widthfloat, optional: Value to calculate the shift position of the BarPlot. By default it is 1.0.

Returns:

graphCollectionsequence of two Graph containing a barplot: The first graph drawing the sensitivity of the Hasofer Reliability Index to the parameters of the marginals of the probabilistic input vector. The second graph drawing the sensitivity of the Hasofer Reliability Index to the parameters of the dependence structure of the probabilistic input vector.

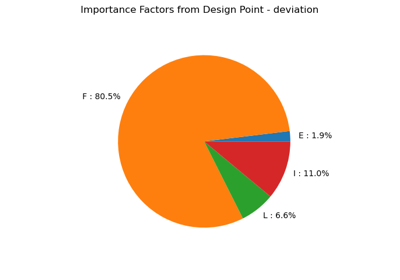
drawImportanceFactors(*args)¶

Draw the importance factors.

Parameters:

typeint, optional: See getImportanceFactors()

Returns:

graphGraph: Pie of the importance factors of the probabilistic variables.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getEventProbabilityBreitung()¶

Accessor to the failure probability $P_{Breitung}$ .

Returns:

probabilitypositive float: The SORM failure probability $P_{Breitung}$ according to the Breitung approximation.

getEventProbabilityHohenbichler()¶

Accessor to the failure probability $P_{Hohenbichler}$ .

Returns:

probabilitypositive float: The SORM failure probability $P_{Hohenbichler}$ according to the Hohenbichler approximation.

getEventProbabilityTvedt()¶

Accessor to the failure probability $P_{Tvedt}$ .

Returns:

probabilitypositive float: The SORM failure probability $P_{Tvedt}$ according to the Tvedt approximation.

getGeneralisedReliabilityIndexBreitung()¶

Accessor to the Generalised Reliability Index Breitung.

Returns:

indexfloat: Generalised reliability index evaluated from the Breitung SORM failure probability.

$\beta_{Breitung} = \left \{ \begin{array}{ll} \displaystyle -\Phi(P_{Breitung}) & \text{if the standard space origin is not in the failure space} \\ \displaystyle \Phi(P_{Breitung}) & \text{otherwise} \end{array} \right.$

getGeneralisedReliabilityIndexHohenbichler()¶

Accessor to the Generalised Reliability Index Hohenbichler.

Returns:

indexfloat: Generalised reliability index evaluated from the Hohenbichler SORM failure probability.

$\beta_{Hohenbichler} = \left \{ \begin{array}{ll} \displaystyle -\Phi(P_{Hohenbichler}) & \text{if the standard space origin is not in the failure space} \\ \displaystyle \Phi(P_{Hohenbichler}) & \text{otherwise} \end{array} \right.$

getGeneralisedReliabilityIndexTvedt()¶

Accessor to the Generalised Reliability Index Tvedt.

Returns:

indexfloat: Generalised reliability index evaluated from the Tvedt SORM failure probability.

$\beta_{Tvedt} = \left \{ \begin{array}{ll} \displaystyle -\Phi(P_{Tvedt}) & \text{if the standard space origin is not in the failure space} \\ \displaystyle \Phi(P_{Tvedt}) & \text{otherwise} \end{array} \right.$

getHasoferReliabilityIndex()¶

Accessor to the Hasofer Reliability Index.

Returns:

indexfloat: Hasofer Reliability Index which is the distance of the design point from the origin of the standard space $\beta_{HL}=||\vect{u}^*||$ .

getHasoferReliabilityIndexSensitivity()¶

Accessor to the sensitivities of the Hasofer Reliability Index.

Returns:

sensitivityPointWithDescription: Sequence containing the sensitivities of the Hasofer Reliability Index to the parameters of the probabilistic input vector (marginals and dependence structure) with a description for each component.

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getImportanceFactors(*args)¶

Accessor to the importance factors.

Parameters:

typeint, optional

When ot.AnalyticalResult.ELLIPTICAL, the importance factors are evaluated as the square of the co-factors of the design point in the elliptical space of the iso-probabilistic transformation (Y-space).
When ot.AnalyticalResult.CLASSICAL they are evaluated as the square of the co-factors of the design point in the U-space.
When ot.AnalyticalResult.PHYSICAL, the importance factors are evaluated as the square of the physical sensitivities.

By default type = ot.AnalyticalResult.ELLIPTICAL.

Returns:

factorsPointWithDescription: Sequence containing the importance factors with a description for each component.

Notes

If the importance factors are evaluated as the square of the co-factors of the design point in the U-space :

$\alpha_i^2 = \frac{(u_i^*)^2} {\beta_{HL}^2}$
If the importance factors are evaluated as the square of the co-factors of the design point in the Y-space :

$\alpha_i^2 = \frac{(y_i^*)^2} {\|\vect{y}^*\|^2}$

where

$Y^* = \left( \begin{array}{c} E^{-1}\circ F_1(X_1^*) \\ E^{-1}\circ F_2(X_2^*) \\ \vdots \\ E^{-1}\circ F_n(X_n^*) \end{array} \right)$

with $\vect{X}^*$ is the design point in the physical space and $E$ the univariate standard CDF of the elliptical space. In the case where the input distribution of $\vect{X}$ has an elliptical copula $C_E$ , then $E$ has the same type as $C_E$ . In the case where the input distribution of $\vect{X}$ has a copula $C$ which is not elliptical, then $E=\Phi$ where $\Phi$ is the CDF of the standard normal.
If the importance factors are evaluated as the square of the physical sensitivities :

$\alpha_i^2 = \displaystyle \frac{s_i^2}{{\|s\|}^2}$

where

$s_i = \displaystyle \frac{\partial \beta}{\partial x_i} (x^*) = \sum_{j=1}^n \frac{\partial \beta}{\partial u_i} \frac{\partial u_j}{\partial x_i} (x^*)$

getIsStandardPointOriginInFailureSpace()¶

Accessor to know if the standard point origin is in the failure space.

Returns:

isInFailureSpacebool: Indicates whether the origin of the standard space is in the failure space.

getLimitStateVariable()¶

Accessor to the event of which the probability is calculated.

Returns:

limitStateVariableRandomVector: Event of which the probability is calculated.

getMeanPointInStandardEventDomain()¶

Accessor to the mean point in the standard event domain.

Returns:

meanPointPoint: Mean point of the standard space distribution restricted to the event domain: $\displaystyle \frac{1}{E_1(-\beta)}\int_{\beta}^{\infty} u_1 p_1(u_1)\di{u_1}$ where $E_1$ is the spheric univariate distribution of the standard space and $\beta$ the reliability index.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOptimizationResult()¶

Accessor to the result of the optimization problem.

Returns:

resultOptimizationResult: Contains the design point in the standard space and information concerning the convergence of the optimization algorithm.

getPhysicalSpaceDesignPoint()¶

Accessor to the design point in the physical space.

Returns:

designPointPoint: Design point in the physical space resulting from the optimization algorithm.

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getSortedCurvatures()¶

Accessor to the sorted curvatures.

Returns:

curvaturesPoint: Curvatures of the standard limite state function at the standard design point $(\kappa_i)_{1 \leq i \leq n-1}$ with $n$ the dimension of the random vector $\vect{X}$ .

getStandardSpaceDesignPoint()¶

Accessor to the design point in the standard space.

Returns:

designPointPoint: Design point in the standard space resulting from the optimization algorithm.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

setIsStandardPointOriginInFailureSpace(isStandardPointOriginInFailureSpace)¶

Accessor to specify if the standard point origin is in the failure space.

Parameters:

isInFailureSpacebool: Indicates whether the origin of the standard space is in the failure space.

setMeanPointInStandardEventDomain(meanPointInStandardEventDomain)¶

Accessor to the mean point in the standard event domain.

Parameters:

meanPointsequence of float: Mean point of the standard space distribution restricted to the event domain: $\displaystyle \frac{1}{E_1(-\beta)}\int_{\beta}^{\infty} u_1 p_1(u_1)\di{u_1}$ where $E_1$ is the spheric univariate distribution of the standard space and $\beta$ the reliability index.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setOptimizationResult(optimizationResult)¶

Accessor to the result of the optimization problem.

Parameters:

resultOptimizationResult: Contains the design point in the standard space and information concerning the convergence of the optimization algorithm.

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters:

idint: Internal unique identifier.

setStandardSpaceDesignPoint(standardSpaceDesignPoint)¶

Accessor to the design point in the standard space.

Parameters:

designPointsequence of float: Design point in the standard space resulting from the optimization algorithm.

setVisibility(visible)¶

Accessor to the object’s visibility state.

Parameters:

visiblebool: Visibility flag.

Examples using the class¶

Use the FORM - SORM algorithms

An illustrated example of a FORM probability estimate

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

SORMResult¶

Examples using the class¶