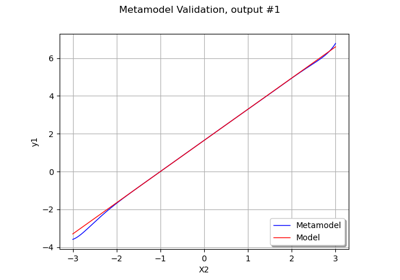
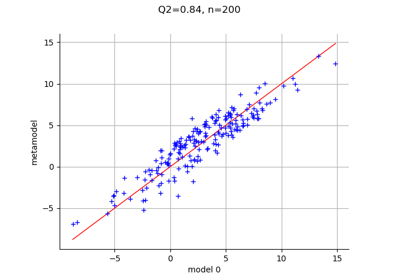
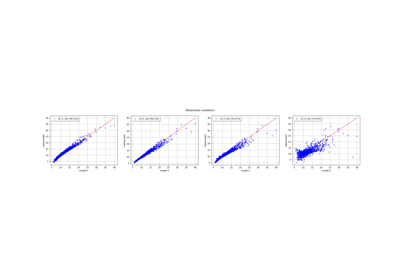
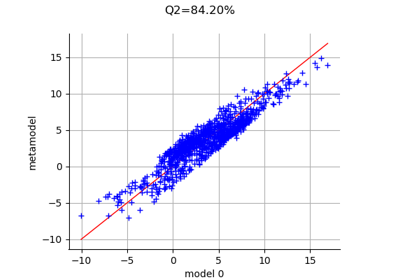
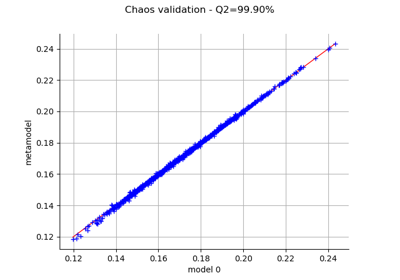
FunctionalChaosResult¶
- class FunctionalChaosResult(*args)¶
Functional chaos result.
Returned by functional chaos algorithms, see
FunctionalChaosAlgorithm.- Parameters:
- sampleX2-d sequence of float
Input sample of
.
- sampleY2-d sequence of float
Output sample of
.
- distribution
Distribution Distribution of the random vector
- transformation
Function The function that maps the physical input
to the standardized input
.
- inverseTransformation
Function The function that maps standardized input
to the the physical input
.
- orthogonalBasis
OrthogonalBasis The multivariate orthogonal basis.
- indicessequence of int
The indices of the selected basis function within the orthogonal basis.
- alpha_k2-d sequence of float
The coefficients of the functional chaos expansion.
- Psi_ksequence of
Function The functions of the multivariate basis selected by the algorithm.
- residualssequence of float,
For each output component, the residual is the square root of the sum of squared differences between the model and the meta model, divided by the sample size.
- relativeErrorssequence of float,
The relative error is the empirical error divided by the sample variance of the output.
Notes
Let
be the sample size. Let
be the dimension of the output of the physical model. For any
and any
, let
be the output of the physical model and let
be the output of the metamodel. For any
, let
be the sample output and let
be the output predicted by the metamodel. The marginal residual is:
for
, where
is the marginal sum of squares:
The marginal relative error is:
for
, where
is the unbiased sample variance of the
-th output.
This structure is created by the method run() of
FunctionalChaosAlgorithm, and obtained thanks to the getResult() method.Methods
Accessor to the object's name.
Get the coefficients.
Get the composed metamodel.
Get the input distribution.
getId()Accessor to the object's id.
Get the indices of the final basis.
Accessor to the input sample.
Get the inverse isoprobabilistic transformation.
Accessor to the metamodel.
getName()Accessor to the object's name.
Get the orthogonal basis.
Accessor to the output sample.
Get the reduced basis.
Accessor to the relative errors.
Accessor to the residuals.
Accessor to the object's shadowed id.
Get the isoprobabilistic transformation.
Accessor to the object's visibility state.
hasName()Test if the object is named.
Test if the object has a distinguishable name.
setInputSample(sampleX)Accessor to the input sample.
setMetaModel(metaModel)Accessor to the metamodel.
setName(name)Accessor to the object's name.
setOutputSample(sampleY)Accessor to the output sample.
setRelativeErrors(relativeErrors)Accessor to the relative errors.
setResiduals(residuals)Accessor to the residuals.
setShadowedId(id)Accessor to the object's shadowed id.
setVisibility(visible)Accessor to the object's visibility state.
- __init__(*args)¶
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getCoefficients()¶
Get the coefficients.
- Returns:
- coefficients2-d sequence of float
Coefficients
.
- getDistribution()¶
Get the input distribution.
- Returns:
- distribution
Distribution Distribution of the input random vector
.
- distribution
- getId()¶
Accessor to the object’s id.
- Returns:
- idint
Internal unique identifier.
- getIndices()¶
Get the indices of the final basis.
- Returns:
- indices
Indices Indices of the elements of the multivariate basis used in the decomposition.
- indices
- getInverseTransformation()¶
Get the inverse isoprobabilistic transformation.
- Returns:
- invTransf
Function such that
.
- invTransf
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getOrthogonalBasis()¶
Get the orthogonal basis.
- Returns:
- basis
OrthogonalBasis Factory of the orthogonal basis.
- basis
- getReducedBasis()¶
Get the reduced basis.
- Returns:
- basislist of
Function Collection of the K functions
used in the decomposition.
- basislist of
- getRelativeErrors()¶
Accessor to the relative errors.
- Returns:
- relativeErrors
Point The relative errors defined as follows for each output of the model:
with
the vector of the
model’s values
and
the metamodel’s values.
- relativeErrors
- getResiduals()¶
Accessor to the residuals.
- Returns:
- residuals
Point The residual values defined as follows for each output of the model:
with
the
model’s values and
the metamodel’s values.
- residuals
- getShadowedId()¶
Accessor to the object’s shadowed id.
- Returns:
- idint
Internal unique identifier.
- getTransformation()¶
Get the isoprobabilistic transformation.
- Returns:
- transformation
Function Transformation
such that
.
- transformation
- getVisibility()¶
Accessor to the object’s visibility state.
- Returns:
- visiblebool
Visibility flag.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- hasVisibleName()¶
Test if the object has a distinguishable name.
- Returns:
- hasVisibleNamebool
True if the name is not empty and not the default one.
- setInputSample(sampleX)¶
Accessor to the input sample.
- Parameters:
- inputSample
Sample The input sample.
- inputSample
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setOutputSample(sampleY)¶
Accessor to the output sample.
- Parameters:
- outputSample
Sample The output sample.
- outputSample
- setRelativeErrors(relativeErrors)¶
Accessor to the relative errors.
- Parameters:
- relativeErrorssequence of float
The relative errors defined as follows for each output of the model:
with
the vector of the
model’s values
and
the metamodel’s values.
- setResiduals(residuals)¶
Accessor to the residuals.
- Parameters:
- residualssequence of float
The residual values defined as follows for each output of the model:
with
the
model’s values and
the metamodel’s values.
- setShadowedId(id)¶
Accessor to the object’s shadowed id.
- Parameters:
- idint
Internal unique identifier.
- setVisibility(visible)¶
Accessor to the object’s visibility state.
- Parameters:
- visiblebool
Visibility flag.
Examples using the class¶
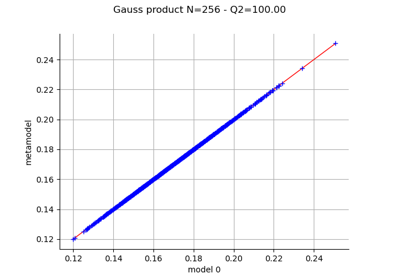
Create a polynomial chaos metamodel by integration on the cantilever beam
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
Example of sensitivity analyses on the wing weight model
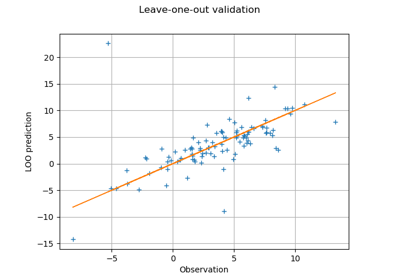
Compute leave-one-out error of a polynomial chaos expansion
 OpenTURNS
OpenTURNS