Convergence of Monte-Carlo to estimate the probability in a reliability problem¶

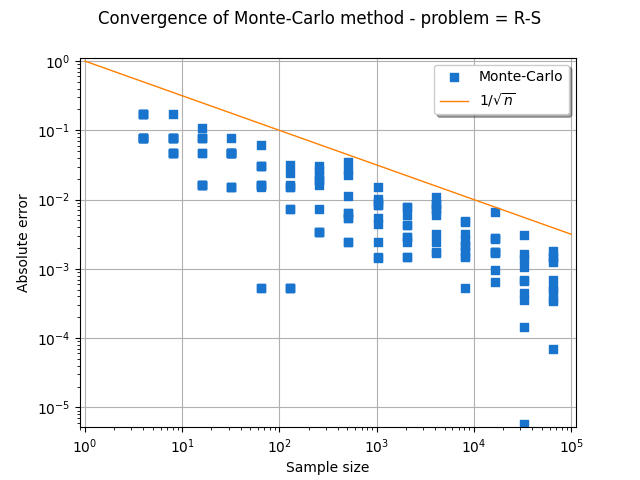
The goal of this document is to present the convergence of the Monte-Carlo algorithm to the exact probability when the sample size increases. This convergence is expressed in terms of absolute error. We show that the rate of convergence is $O(\sqrt{n})$ , where $n$ is the sample size.

import openturns as ot
import openturns.viewer as otv
import numpy as np
import otbenchmark as otb
import time

problem = otb.RminusSReliability()
print(problem)


def ComputeProbabilityFromMonteCarlo(
    problem, coefficientOfVariation=0.1, maximumOuterSampling=1000, blockSize=2
):
    event = problem.getEvent()
    g = event.getFunction()
    # Create the Monte-Carlo algorithm
    algoProb = ot.ProbabilitySimulationAlgorithm(event)
    algoProb.setMaximumOuterSampling(maximumOuterSampling)
    algoProb.setBlockSize(blockSize)
    algoProb.setMaximumCoefficientOfVariation(coefficientOfVariation)
    initialNumberOfFunctionEvaluations = g.getEvaluationCallsNumber()
    algoProb.run()
    # Get the results
    resultAlgo = algoProb.getResult()
    numberOfFunctionEvaluations = (
        g.getEvaluationCallsNumber() - initialNumberOfFunctionEvaluations
    )
    pf = resultAlgo.getProbabilityEstimate()
    level = 0.95
    c95 = resultAlgo.getConfidenceLength(level)
    pmin = pf - 0.5 * c95
    pmax = pf + 0.5 * c95
    print(
        "Number of function calls = %d" % (numberOfFunctionEvaluations),
        ", Pf = %.4f" % (pf),
        ", %.1f %% confidence interval :[%.4f,%.4f] " % (level * 100, pmin, pmax),
    )
    absoluteError = abs(pf - problem.getProbability())
    result = {
        "numberOfFunctionEvaluations": numberOfFunctionEvaluations,
        "pf": pf,
        "pmin": pmin,
        "pmax": pmax,
        "absoluteError": absoluteError,
    }
    return result

name = R-S
event = class=ThresholdEventImplementation antecedent=class=CompositeRandomVector function=class=Function name=Unnamed implementation=class=FunctionImplementation name=Unnamed description=[R,S,y0] evaluationImplementation=class=SymbolicEvaluation name=Unnamed inputVariablesNames=[R,S] outputVariablesNames=[y0] formulas=[R - S] gradientImplementation=class=SymbolicGradient name=Unnamed evaluation=class=SymbolicEvaluation name=Unnamed inputVariablesNames=[R,S] outputVariablesNames=[y0] formulas=[R - S] hessianImplementation=class=SymbolicHessian name=Unnamed evaluation=class=SymbolicEvaluation name=Unnamed inputVariablesNames=[R,S] outputVariablesNames=[y0] formulas=[R - S] antecedent=class=UsualRandomVector distribution=class=JointDistribution name=JointDistribution dimension=2 copula=class=IndependentCopula name=IndependentCopula dimension=2 marginal[0]=class=Normal name=Normal dimension=1 mean=class=Point name=Unnamed dimension=1 values=[4] sigma=class=Point name=Unnamed dimension=1 values=[1] correlationMatrix=class=CorrelationMatrix dimension=1 implementation=class=MatrixImplementation name=Unnamed rows=1 columns=1 values=[1] marginal[1]=class=Normal name=Normal dimension=1 mean=class=Point name=Unnamed dimension=1 values=[2] sigma=class=Point name=Unnamed dimension=1 values=[1] correlationMatrix=class=CorrelationMatrix dimension=1 implementation=class=MatrixImplementation name=Unnamed rows=1 columns=1 values=[1] operator=class=Less name=Unnamed threshold=0
probability = 0.07864960352514257

result = ComputeProbabilityFromMonteCarlo(problem)

Number of function calls = 2000 , Pf = 0.0690 , 95.0 % confidence interval :[0.0554,0.0826]

numberOfPoints = 15  # Number of atomic experiments
numberOfRepetitions = 10  # Number of repetitions of each experiment
sampleSizeAbsoluteErrorTable = ot.Sample(numberOfPoints * numberOfRepetitions, 2)
sampleSizeAbsoluteErrorTable.setDescription(["Sample size", "Absolute error"])

cov = 0.0
startTime = time.time()

maximumOuterSampling = 1
index = 0
for i in range(numberOfPoints):
    maximumOuterSampling *= 2
    for j in range(numberOfRepetitions):
        result = ComputeProbabilityFromMonteCarlo(
            problem,
            coefficientOfVariation=cov,
            maximumOuterSampling=maximumOuterSampling,
        )
        sampleSizeAbsoluteErrorTable[index, 0] = result["numberOfFunctionEvaluations"]
        sampleSizeAbsoluteErrorTable[index, 1] = result["absoluteError"]
        index += 1

Number of function calls = 4 , Pf = 0.2500 , 95.0 % confidence interval :[-0.2978,0.7978]
Number of function calls = 4 , Pf = 0.2500 , 95.0 % confidence interval :[-0.2978,0.7978]
Number of function calls = 4 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 4 , Pf = 0.2500 , 95.0 % confidence interval :[-0.2978,0.7978]
Number of function calls = 4 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 4 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 4 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 4 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 4 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 4 , Pf = 0.2500 , 95.0 % confidence interval :[-0.2978,0.7978]
Number of function calls = 8 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 8 , Pf = 0.1250 , 95.0 % confidence interval :[-0.1623,0.4123]
Number of function calls = 8 , Pf = 0.2500 , 95.0 % confidence interval :[-0.1374,0.6374]
Number of function calls = 8 , Pf = 0.1250 , 95.0 % confidence interval :[-0.1623,0.4123]
Number of function calls = 8 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 8 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 8 , Pf = 0.1250 , 95.0 % confidence interval :[-0.1623,0.4123]
Number of function calls = 8 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 8 , Pf = 0.1250 , 95.0 % confidence interval :[-0.1623,0.4123]
Number of function calls = 8 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 16 , Pf = 0.1250 , 95.0 % confidence interval :[-0.0781,0.3281]
Number of function calls = 16 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 16 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0844,0.2094]
Number of function calls = 16 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0844,0.2094]
Number of function calls = 16 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0844,0.2094]
Number of function calls = 16 , Pf = 0.1250 , 95.0 % confidence interval :[-0.0781,0.3281]
Number of function calls = 16 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 16 , Pf = 0.1875 , 95.0 % confidence interval :[-0.0556,0.4306]
Number of function calls = 16 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 16 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0844,0.2094]
Number of function calls = 32 , Pf = 0.0312 , 95.0 % confidence interval :[-0.0430,0.1055]
Number of function calls = 32 , Pf = 0.1250 , 95.0 % confidence interval :[-0.0186,0.2686]
Number of function calls = 32 , Pf = 0.0312 , 95.0 % confidence interval :[-0.0430,0.1055]
Number of function calls = 32 , Pf = 0.0312 , 95.0 % confidence interval :[-0.0430,0.1055]
Number of function calls = 32 , Pf = 0.0938 , 95.0 % confidence interval :[-0.0321,0.2196]
Number of function calls = 32 , Pf = 0.0312 , 95.0 % confidence interval :[-0.0430,0.1055]
Number of function calls = 32 , Pf = 0.0938 , 95.0 % confidence interval :[-0.0321,0.2196]
Number of function calls = 32 , Pf = 0.0312 , 95.0 % confidence interval :[-0.0430,0.1055]
Number of function calls = 32 , Pf = 0.0938 , 95.0 % confidence interval :[-0.0321,0.2196]
Number of function calls = 32 , Pf = 0.0000 , 95.0 % confidence interval :[0.0000,0.0000]
Number of function calls = 64 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0109,0.1359]
Number of function calls = 64 , Pf = 0.0938 , 95.0 % confidence interval :[0.0048,0.1827]
Number of function calls = 64 , Pf = 0.1094 , 95.0 % confidence interval :[0.0189,0.1999]
Number of function calls = 64 , Pf = 0.0781 , 95.0 % confidence interval :[0.0024,0.1538]
Number of function calls = 64 , Pf = 0.0781 , 95.0 % confidence interval :[0.0024,0.1538]
Number of function calls = 64 , Pf = 0.1406 , 95.0 % confidence interval :[0.0380,0.2433]
Number of function calls = 64 , Pf = 0.1094 , 95.0 % confidence interval :[0.0189,0.1999]
Number of function calls = 64 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0109,0.1359]
Number of function calls = 64 , Pf = 0.1094 , 95.0 % confidence interval :[0.0138,0.2049]
Number of function calls = 64 , Pf = 0.0625 , 95.0 % confidence interval :[-0.0109,0.1359]
Number of function calls = 128 , Pf = 0.0859 , 95.0 % confidence interval :[0.0255,0.1463]
Number of function calls = 128 , Pf = 0.0781 , 95.0 % confidence interval :[0.0204,0.1359]
Number of function calls = 128 , Pf = 0.0938 , 95.0 % confidence interval :[0.0308,0.1567]
Number of function calls = 128 , Pf = 0.0938 , 95.0 % confidence interval :[0.0327,0.1548]
Number of function calls = 128 , Pf = 0.0781 , 95.0 % confidence interval :[0.0204,0.1359]
Number of function calls = 128 , Pf = 0.0547 , 95.0 % confidence interval :[0.0060,0.1034]
Number of function calls = 128 , Pf = 0.0859 , 95.0 % confidence interval :[0.0255,0.1463]
Number of function calls = 128 , Pf = 0.0469 , 95.0 % confidence interval :[0.0017,0.0921]
Number of function calls = 128 , Pf = 0.0781 , 95.0 % confidence interval :[0.0204,0.1359]
Number of function calls = 128 , Pf = 0.0625 , 95.0 % confidence interval :[0.0106,0.1144]
Number of function calls = 256 , Pf = 0.0859 , 95.0 % confidence interval :[0.0439,0.1279]
Number of function calls = 256 , Pf = 0.1055 , 95.0 % confidence interval :[0.0585,0.1524]
Number of function calls = 256 , Pf = 0.1094 , 95.0 % confidence interval :[0.0635,0.1553]
Number of function calls = 256 , Pf = 0.0977 , 95.0 % confidence interval :[0.0530,0.1423]
Number of function calls = 256 , Pf = 0.0820 , 95.0 % confidence interval :[0.0410,0.1231]
Number of function calls = 256 , Pf = 0.0625 , 95.0 % confidence interval :[0.0258,0.0992]
Number of function calls = 256 , Pf = 0.0977 , 95.0 % confidence interval :[0.0530,0.1423]
Number of function calls = 256 , Pf = 0.0820 , 95.0 % confidence interval :[0.0424,0.1216]
Number of function calls = 256 , Pf = 0.1016 , 95.0 % confidence interval :[0.0567,0.1464]
Number of function calls = 256 , Pf = 0.0820 , 95.0 % confidence interval :[0.0410,0.1231]
Number of function calls = 512 , Pf = 0.0898 , 95.0 % confidence interval :[0.0602,0.1195]
Number of function calls = 512 , Pf = 0.0762 , 95.0 % confidence interval :[0.0476,0.1047]
Number of function calls = 512 , Pf = 0.0840 , 95.0 % confidence interval :[0.0544,0.1136]
Number of function calls = 512 , Pf = 0.0723 , 95.0 % confidence interval :[0.0450,0.0996]
Number of function calls = 512 , Pf = 0.1055 , 95.0 % confidence interval :[0.0727,0.1382]
Number of function calls = 512 , Pf = 0.1016 , 95.0 % confidence interval :[0.0694,0.1338]
Number of function calls = 512 , Pf = 0.0723 , 95.0 % confidence interval :[0.0444,0.1001]
Number of function calls = 512 , Pf = 0.0762 , 95.0 % confidence interval :[0.0484,0.1039]
Number of function calls = 512 , Pf = 0.0840 , 95.0 % confidence interval :[0.0549,0.1131]
Number of function calls = 512 , Pf = 0.1133 , 95.0 % confidence interval :[0.0794,0.1472]
Number of function calls = 1024 , Pf = 0.0811 , 95.0 % confidence interval :[0.0606,0.1015]
Number of function calls = 1024 , Pf = 0.0693 , 95.0 % confidence interval :[0.0502,0.0884]
Number of function calls = 1024 , Pf = 0.0771 , 95.0 % confidence interval :[0.0574,0.0969]
Number of function calls = 1024 , Pf = 0.0684 , 95.0 % confidence interval :[0.0494,0.0873]
Number of function calls = 1024 , Pf = 0.0703 , 95.0 % confidence interval :[0.0512,0.0894]
Number of function calls = 1024 , Pf = 0.0869 , 95.0 % confidence interval :[0.0659,0.1079]
Number of function calls = 1024 , Pf = 0.0801 , 95.0 % confidence interval :[0.0596,0.1006]
Number of function calls = 1024 , Pf = 0.0635 , 95.0 % confidence interval :[0.0453,0.0817]
Number of function calls = 1024 , Pf = 0.0840 , 95.0 % confidence interval :[0.0635,0.1045]
Number of function calls = 1024 , Pf = 0.0742 , 95.0 % confidence interval :[0.0549,0.0936]
Number of function calls = 2048 , Pf = 0.0728 , 95.0 % confidence interval :[0.0591,0.0864]
Number of function calls = 2048 , Pf = 0.0830 , 95.0 % confidence interval :[0.0683,0.0977]
Number of function calls = 2048 , Pf = 0.0815 , 95.0 % confidence interval :[0.0671,0.0960]
Number of function calls = 2048 , Pf = 0.0830 , 95.0 % confidence interval :[0.0684,0.0976]
Number of function calls = 2048 , Pf = 0.0815 , 95.0 % confidence interval :[0.0669,0.0962]
Number of function calls = 2048 , Pf = 0.0771 , 95.0 % confidence interval :[0.0630,0.0913]
Number of function calls = 2048 , Pf = 0.0708 , 95.0 % confidence interval :[0.0572,0.0844]
Number of function calls = 2048 , Pf = 0.0864 , 95.0 % confidence interval :[0.0716,0.1013]
Number of function calls = 2048 , Pf = 0.0762 , 95.0 % confidence interval :[0.0621,0.0902]
Number of function calls = 2048 , Pf = 0.0771 , 95.0 % confidence interval :[0.0631,0.0912]
Number of function calls = 4096 , Pf = 0.0701 , 95.0 % confidence interval :[0.0605,0.0796]
Number of function calls = 4096 , Pf = 0.0769 , 95.0 % confidence interval :[0.0669,0.0869]
Number of function calls = 4096 , Pf = 0.0803 , 95.0 % confidence interval :[0.0701,0.0905]
Number of function calls = 4096 , Pf = 0.0701 , 95.0 % confidence interval :[0.0605,0.0797]
Number of function calls = 4096 , Pf = 0.0676 , 95.0 % confidence interval :[0.0582,0.0770]
Number of function calls = 4096 , Pf = 0.0754 , 95.0 % confidence interval :[0.0655,0.0853]
Number of function calls = 4096 , Pf = 0.0728 , 95.0 % confidence interval :[0.0630,0.0825]
Number of function calls = 4096 , Pf = 0.0857 , 95.0 % confidence interval :[0.0753,0.0961]
Number of function calls = 4096 , Pf = 0.0762 , 95.0 % confidence interval :[0.0662,0.0861]
Number of function calls = 4096 , Pf = 0.0710 , 95.0 % confidence interval :[0.0614,0.0807]
Number of function calls = 8192 , Pf = 0.0771 , 95.0 % confidence interval :[0.0701,0.0842]
Number of function calls = 8192 , Pf = 0.0765 , 95.0 % confidence interval :[0.0695,0.0836]
Number of function calls = 8192 , Pf = 0.0802 , 95.0 % confidence interval :[0.0730,0.0874]
Number of function calls = 8192 , Pf = 0.0769 , 95.0 % confidence interval :[0.0699,0.0839]
Number of function calls = 8192 , Pf = 0.0781 , 95.0 % confidence interval :[0.0710,0.0852]
Number of function calls = 8192 , Pf = 0.0818 , 95.0 % confidence interval :[0.0745,0.0891]
Number of function calls = 8192 , Pf = 0.0737 , 95.0 % confidence interval :[0.0668,0.0807]
Number of function calls = 8192 , Pf = 0.0740 , 95.0 % confidence interval :[0.0670,0.0809]
Number of function calls = 8192 , Pf = 0.0813 , 95.0 % confidence interval :[0.0740,0.0886]
Number of function calls = 8192 , Pf = 0.0765 , 95.0 % confidence interval :[0.0695,0.0836]
Number of function calls = 16384 , Pf = 0.0815 , 95.0 % confidence interval :[0.0763,0.0866]
Number of function calls = 16384 , Pf = 0.0780 , 95.0 % confidence interval :[0.0730,0.0830]
Number of function calls = 16384 , Pf = 0.0769 , 95.0 % confidence interval :[0.0719,0.0819]
Number of function calls = 16384 , Pf = 0.0804 , 95.0 % confidence interval :[0.0753,0.0855]
Number of function calls = 16384 , Pf = 0.0760 , 95.0 % confidence interval :[0.0710,0.0810]
Number of function calls = 16384 , Pf = 0.0759 , 95.0 % confidence interval :[0.0709,0.0808]
Number of function calls = 16384 , Pf = 0.0770 , 95.0 % confidence interval :[0.0720,0.0820]
Number of function calls = 16384 , Pf = 0.0777 , 95.0 % confidence interval :[0.0727,0.0827]
Number of function calls = 16384 , Pf = 0.0769 , 95.0 % confidence interval :[0.0719,0.0819]
Number of function calls = 16384 , Pf = 0.0853 , 95.0 % confidence interval :[0.0801,0.0906]
Number of function calls = 32768 , Pf = 0.0793 , 95.0 % confidence interval :[0.0757,0.0829]
Number of function calls = 32768 , Pf = 0.0786 , 95.0 % confidence interval :[0.0751,0.0822]
Number of function calls = 32768 , Pf = 0.0790 , 95.0 % confidence interval :[0.0754,0.0826]
Number of function calls = 32768 , Pf = 0.0788 , 95.0 % confidence interval :[0.0752,0.0824]
Number of function calls = 32768 , Pf = 0.0773 , 95.0 % confidence interval :[0.0737,0.0808]
Number of function calls = 32768 , Pf = 0.0791 , 95.0 % confidence interval :[0.0755,0.0827]
Number of function calls = 32768 , Pf = 0.0797 , 95.0 % confidence interval :[0.0761,0.0833]
Number of function calls = 32768 , Pf = 0.0803 , 95.0 % confidence interval :[0.0767,0.0839]
Number of function calls = 32768 , Pf = 0.0756 , 95.0 % confidence interval :[0.0721,0.0791]
Number of function calls = 32768 , Pf = 0.0793 , 95.0 % confidence interval :[0.0758,0.0829]
Number of function calls = 65536 , Pf = 0.0781 , 95.0 % confidence interval :[0.0756,0.0807]
Number of function calls = 65536 , Pf = 0.0791 , 95.0 % confidence interval :[0.0766,0.0817]
Number of function calls = 65536 , Pf = 0.0768 , 95.0 % confidence interval :[0.0743,0.0793]
Number of function calls = 65536 , Pf = 0.0801 , 95.0 % confidence interval :[0.0776,0.0827]
Number of function calls = 65536 , Pf = 0.0783 , 95.0 % confidence interval :[0.0758,0.0808]
Number of function calls = 65536 , Pf = 0.0774 , 95.0 % confidence interval :[0.0749,0.0799]
Number of function calls = 65536 , Pf = 0.0801 , 95.0 % confidence interval :[0.0775,0.0826]
Number of function calls = 65536 , Pf = 0.0793 , 95.0 % confidence interval :[0.0768,0.0819]
Number of function calls = 65536 , Pf = 0.0787 , 95.0 % confidence interval :[0.0762,0.0812]
Number of function calls = 65536 , Pf = 0.0783 , 95.0 % confidence interval :[0.0758,0.0808]

elapsedTime = time.time() - startTime
print("Elapsed = %.2f (s)" % (elapsedTime))

Elapsed = 3.58 (s)

sampleSizeArray = [int(n) for n in np.logspace(0.0, 5.0)]
expectedConvergence = [1.0 / np.sqrt(n) for n in sampleSizeArray]

title = "Convergence of Monte-Carlo method - problem = %s" % (problem.getName())
graph = ot.Graph(title, "Sample size", "Absolute error", True, "topright")
curve = ot.Cloud(sampleSizeAbsoluteErrorTable, "blue", "fsquare", "")
curve.setLegend("Monte-Carlo")
graph.add(curve)
curve = ot.Curve(sampleSizeArray, expectedConvergence)
curve.setLegend(r"$1/\sqrt{n}$")
graph.add(curve)
graph.setLogScale(ot.GraphImplementation.LOGXY)
graph.setColors(["dodgerblue3", "darkorange1"])
_ = otv.View(graph)

Convergence of Monte-Carlo method - problem = R-S

otv.View.ShowAll()

Total running time of the script: (0 minutes 4.178 seconds)

otbenchmark

Module otbenchmark

Table of Contents

Previous topic

Next topic

This Page

Convergence of Monte-Carlo to estimate the probability in a reliability problem¶