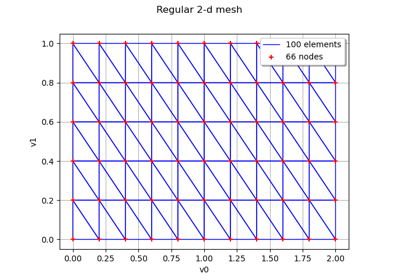
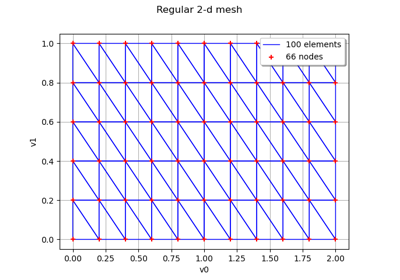
IntervalMesher¶
(Source code, png)
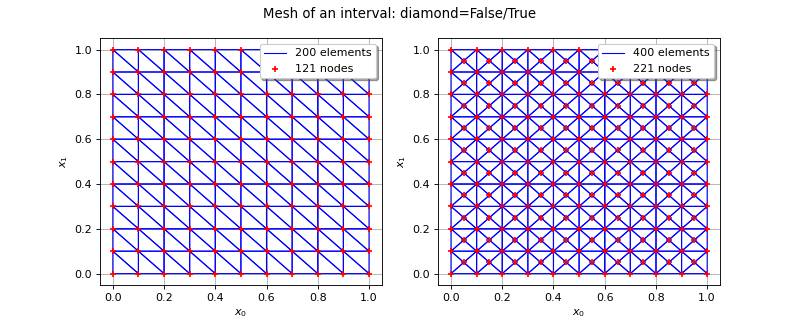
- class IntervalMesher(*args)¶
Creation of mesh of box type.
- Parameters:
- discretizationsequence of int.
Number of intervals in each direction of the box.
Examples
Create a mesh:
>>> import openturns as ot >>> mesher = ot.IntervalMesher([5, 10]) >>> lowerbound = [0.0, 0.0] >>> upperBound = [2.0, 4.0] >>> interval = ot.Interval(lowerbound, upperBound) >>> mesh = mesher.build(interval)
Methods
build(*args)Build the mesh of box type.
Accessor to the object's name.
Accessor to the discretization.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setDiscretization(discretization)Accessor to the discretization.
setName(name)Accessor to the object's name.
- __init__(*args)¶
- build(*args)¶
Build the mesh of box type.
- Parameters:
- interval
Interval The interval to mesh, of dimension equal to the dimension of discretization.
- diamondbool
A flag telling if one want the usual mesh (rectangular cells cut along a diagonal in dimension 2) or a diamond like mesh (rectangular cells cut into 4 triangles with the center of the cell as shared vertex). Default is IntervalMesher-UseDiamond, see
ResourceMap.
- interval
- Returns:
- mesh
Mesh The mesh built.
- mesh
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getDiscretization()¶
Accessor to the discretization.
- Returns:
- discretization
Indices Number of intervals in each direction of the box.
- discretization
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setDiscretization(discretization)¶
Accessor to the discretization.
- Parameters:
- discretizationsequence of int
Number of intervals in each direction of the box.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
 OpenTURNS
OpenTURNS