GaussLegendre¶

(Source code, png)

class GaussLegendre(*args)¶

Tensorized integration algorithm of Gauss-Legendre.

Available constructors:

GaussLegendre(dimension=1)

GaussLegendre(discretization)

Parameters:

dimensionint, $dimension>0$

The input dimension of the functions to integrate.

discretizationsequence of int

The number of nodes in each dimension. The sequence must be non-empty and must contain only positive values.

The default discretization is stored as the GaussLegendre- DefaultMarginalIntegrationPointsNumber ResourceMap key, which is used for each dimension.

Methods

`getClassName`()	Accessor to the object's name.
`getDiscretization`()	Accessor to the discretization of the tensorized rule.
`getName`()	Accessor to the object's name.
`getNodes`()	Accessor to the integration nodes in $[0,1]^d$ .
`getWeights`()	Accessor to the integration weights for nodes in $[0,1]^d$ .
`hasName`()	Test if the object is named.
`integrate`(*args)	Evaluation of the integral of $f$ on an interval.
`integrateWithNodes`(function, interval)	Evaluation of the integral of $f$ on an interval with nodes.
`setName`(name)	Accessor to the object's name.

See also

GaussProductExperiment, TensorProductExperiment

Notes

We consider a function $f: \Rset^\inputDim \mapsto \Rset^\outputDim$ and a domain $\set{D} = [\vect{a}, \vect{b}]$ where $\vect{a}, \vect{b} \in \Rset^\inputDim$ . The Gauss-Legendre algorithm approximates the definite integral:

(1)¶ $\int_{\vect{a}}^\vect{b} f(\vect{t})\di{\vect{t}}$

For $i \in \{1, ..., \inputDim\}$ , let $N_i \in \Nset$ be the number of marginal nodes of the univariate Gauss-Legendre quadrature. The algorithm uses a fixed tensorized Gauss-Legendre approximation based on the tensor-product Gauss quadrature using $N_1, ..., N_\inputDim \in \Nset$ marginal nodes. In other words, this algorithm uses an anisotropic quadrature rule, i.e. the number of nodes in each marginal dimension are not necessarily equal.

In order to get a more straightforward access to the nodes and weights, please use the GaussProductExperiment class. In order to create a more general tensor product quadrature, please use the TensorProductExperiment class.

Quadrature rule

We detail here the quadrature rule. As integral (1) is computed for each marginal of the integrand function, we consider now that $f: \Rset^\inputDim \mapsto \Rset$ . The approximated integral is:

(2)¶ $\int_{\vect{a}}^{\vect{b}} f(\vect{t}) \di{\vect{t}} = \sum_{n_1=1}^{N_1} \dots \sum_{n_d=1}^{N_d}\left( \prod_{i=1}^d w^{N_i}_{n_i}\right) f(\xi^{N_1}_{n_1},\dots,\xi^{N_d}_{n_d})$

where $\xi^{N_i}_{n_i}$ is the $n_i$ -th node computed from the $N_i$ -points Gauss- Legendre 1D integration rule and $w^{N_i}_{n_i} > 0$ the associated weight.

The total number of nodes is the product of marginal number of nodes:

$\prod_{i = 1}^\inputDim N_i.$

To use that approximation, the integration variables are scaled to the domain $[0,1]^d$ with the mapping function $\varphi$ defined by:

(3)¶ $\varphi : & [0,1]^d \rightarrow [\vect{a}, \vect{b}]\\ & \vect{x} \rightarrow \vect{t} = \vect{a} + (\vect{b}-\vect{a}) \vect{x}$

where each component is $t_i = a_i + (b_i-a_i)x_i$ for $1 \leq i \leq d$ .

Let $|\vect{b}-\vect{a}| = \prod_{i=1}^d (b_i-a_i)$ be the volume of the domain $[\vect{a}, \vect{b}]$ . Then, we have:

(4)¶ $\int_{\vect{a}}^{\vect{b}} f(\vect{t})\di{\vect{t}} & = \int_{[0,1]^d} |\vect{b}-\vect{a}| f\left( \vect{a} + (\vect{b}-\vect{a})\vect{x}\right)\di{\vect{x}} \\ & = \int_{[0,1]^d} \tilde{f}(\vect{x})\di{\vect{x}}$

where we introduced the scaled function $\tilde{f}$ on $[0,1]^d$ defined by:

(5)¶ $\tilde{f}(\vect{x}) = |\vect{b}-\vect{a}| f \circ \varphi ( \vect{x} )$

Then, the Gauss-Legendre quadrature rule is applied to the function $\tilde{f}$ defined on $[0,1]^d$ . We denote by $\tilde{\xi}^{N_i}_{n_i}$ the $n_i$ -th node of the $N_i$ -points Gauss-Legendre 1D integration rule and $\tilde{w}^{N_i}_{n_i}$ the associated weight. Then we have:

(6)¶ $\int_{[0,1]^d} \tilde{f}(\vect{x})\di{\vect{x}} = \sum_{n_1=1}^{N_1}\dots \sum_{n_d=1}^{N_d} \left(\prod_{i=1}^d \tilde{w}^{N_i}_{n_i}\right)\tilde{f}(\tilde{\xi}^{N_1}_{n_1},\dots,\tilde{\xi}^{N_d} _{n_d})$

Using (5) and (6), we get:

(7)¶ $\int_{\vect{a}}^{\vect{b}} f(\vect{t})\di{\vect{t}} & = \sum_{n_1=1}^{N_1}\dots \sum_{n_d=1}^{N_d} \left(\prod_{i=1}^d \tilde{w}^{N_i}_{n_i}\right) |\vect{b}-\vect{a}| f\left( a_1 + (b_1-a_1)\tilde{\xi} ^{N_1}_{n_1},\dots,a_d + (b_d-a_d)\tilde{\xi}^{N_d}_{n_d}\right)\\ & = \sum_{n_1=1}^{N_1}\dots \sum_{n_d=1}^{N_d}\left(\prod_{i=1}^d \tilde{w}^{N_i}_{n_i}(b_i-a_i)\right) f\left( a_1 + (b_1-a_1)\tilde{\xi}^{N_1}_{n_1},\dots,a_d + (b_d-a_d)\tilde{\xi}^{N_d}_{n_d}\right)$

Then, the nodes used to compute approximation (2) are defined as follows:

(8)¶ $\xi^{N_i}_{n_i} = a_i + (b_i-a_i)\tilde{\xi}^{N_i}_{n_i}$

and the weights are:

(9)¶ $w^{N_i}_{n_i} = (b_i-a_i)\tilde{w}^{N_i}_{n_i}$

Polynomial exactness

The Gauss-Legendre quadrature rule is exact for polynomials up to some degree. More precisely, for any $m_i \in \Nset$ , let $\mathcal{P}_{m_i}^{(1)}$ be the set of mono-variable polynomials of degree lower or equal to $m_i$ . Consider the tensor product of 1D polynomials:

$\bigotimes_{i = 1}^\inputDim \mathcal{P}_{m_i}^{(1)} = \left\{ (x_1, ..., x_\inputDim)\in\Rset^\inputDim \rightarrow \prod_{i = 1}^\inputDim p_i(x_i) \in \Rset, \quad p_i \in \mathcal{P}_{m_i}^{(1)} \right\}.$

Therefore the Gauss-Legendre tensorized quadrature is exact for all polynomials of the vector space:

$\bigotimes_{i = 1}^\inputDim \mathcal{P}_{2 n_i - 1}^{(1)}.$

Examples

Create a Gauss-Legendre algorithm in dimension 2.

>>> import openturns as ot
>>> algo = ot.GaussLegendre(2)

Create a Gauss-Legendre algorithm in dimension 3 with 2 nodes for $x_1$ , 4 nodes for $x_2$ and 5 nodes for $x_3$ .

>>> algo = ot.GaussLegendre([2, 4, 5])

We show how to use this method to evaluate the following integral:

$\int_{[0,1]^3} x_1^5 x_2^3 x_3^7 d\vect{x}$

First, we use the default number of nodes as defined in the ResourceMap.

>>> dimension = 3
>>> bounds = ot.Interval([0.0] * dimension, [1.0] * dimension)
>>> polynomial = ot.SymbolicFunction(['x1', 'x2', 'x3'], ['x1^5 * x2^3 * x3^7'])
>>> algo = ot.GaussLegendre(dimension)
>>> computedIntegral = algo.integrate(polynomial, bounds)
>>> print(computedIntegral)
[0.00520833]

In the previous example, we used the default number of nodes in each dimension, as defined by the ResourceMap. In the next example, we set the number of marginal nodes: we use 3 nodes for $x_1$ , 2 nodes for $x_2$ , 4 nodes for $x_3$ . In this case, the vector space for which the Gauss-Legendre quadrature rule is exact is $\mathcal{P}_5 \otimes \mathcal{P}_3 \otimes \mathcal{P}_7$ . In other words, we test the quadrature rule against the polynomial with maximum possible marginal degrees.

>>> dimension = 3
>>> bounds = ot.Interval([0.0] * dimension, [1.0] * dimension)
>>> polynomial = ot.SymbolicFunction(['x1', 'x2', 'x3'], ['x1^5 * x2^3 * x3^7'])
>>> algo = ot.GaussLegendre([3, 2, 4])
>>> computedIntegral = algo.integrate(polynomial, bounds)
>>> print(computedIntegral)
[0.00520833]

__init__(*args)¶

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDiscretization()¶

Accessor to the discretization of the tensorized rule.

Returns:

discretizationIndices: The number of integration point in each dimension.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getNodes()¶

Accessor to the integration nodes in $[0,1]^d$ .

Returns:

nodesSample: The tensorized Gauss-Legendre integration nodes on $[0,1]^\inputDim$ where $d>0$ is the dimension of the integration algorithm.

Notes

The nodes are those associated to the scaled function: $(\tilde{\xi}^{N_i}_{n_i})$ .

getWeights()¶

Accessor to the integration weights for nodes in $[0,1]^d$ .

Returns:

weightsPoint: The tensorized Gauss-Legendre integration weights on $[0,1]^\inputDim$ where $d>0$ is the dimension of the integration algorithm.

Notes

The weights are those associated to the scaled function: $(\tilde{w}^{N_i}_{n_i})$ .

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

integrate(*args)¶

Evaluation of the integral of $f$ on an interval.

Available usages:: integrate(f, interval)

Parameters:

fFunction, $f: \Rset^\inputDim \mapsto \Rset^\outputDim$: The integrand function.
intervalInterval, $interval \in \Rset^\inputDim$: The integration domain.

Returns:

valuePoint: Approximation of the integral.

Examples

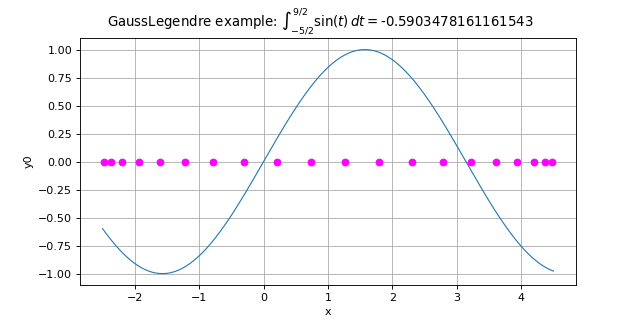
>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x'], ['sin(x)'])
>>> a = -2.5
>>> b = 4.5
>>> algoGL = ot.GaussLegendre([10])
>>> value = algoGL.integrate(f, ot.Interval(a, b))[0]
>>> print(value)
-0.590...

integrateWithNodes(function, interval)¶

Evaluation of the integral of $f$ on an interval with nodes.

Parameters:

fFunction, $f: \Rset^\inputDim \mapsto \Rset^\outputDim$: The integrand function.
intervalInterval, $interval \in \Rset^\inputDim$: The integration domain.

Returns:

valuePoint: Approximation of the integral.
nodesSample.: The integration nodes defined in (8).

Notes

The nodes are those associated to the function: $(\xi^{N_i}_{n_i})$ .

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x'], ['sin(x)'])
>>> a = -2.5
>>> b = 4.5
>>> algoGL = ot.GaussLegendre([10])
>>> value, nodes = algoGL.integrateWithNodes(f, ot.Interval(a, b))
>>> print(value[0])
-0.590...
>>> print(nodes)
0 : [ -2.40867  ]
1 : [ -2.02772  ]
2 : [ -1.37793  ]
3 : [ -0.516884 ]
4 : [  0.47894  ]
5 : [  1.52106  ]
6 : [  2.51688  ]
7 : [  3.37793  ]
8 : [  4.02772  ]
9 : [  4.40867  ]

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

GaussLegendre¶