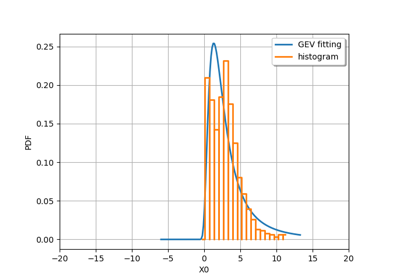
GeneralizedParetoFactory¶

(Source code, png)

class GeneralizedParetoFactory(*args)¶

Generalized Pareto factory.

Methods

`build`(*args)	Build the distribution.
`buildAsGeneralizedPareto`(*args)	Build the distribution as a GeneralizedPareto type.
`buildCovariates`(*args)	Estimate a GPD from covariates.
`buildEstimator`(*args)	Build the distribution and the parameter distribution.
`buildMethodOfExponentialRegression`(sample)	Build the distribution based on the exponential regression estimator.
`buildMethodOfLikelihoodMaximization`(sample, u)	Estimate the distribution with the maximum likelihood method.
`buildMethodOfLikelihoodMaximizationEstimator`(...)	Estimate the distribution and the parameter distribution with the maximum likelihood method.
`buildMethodOfMoments`(sample)	Build the distribution based on the method of moments estimator.
`buildMethodOfProbabilityWeightedMoments`(sample)	Build the distribution based on the probability weighted moments estimator.
`buildMethodOfXiProfileLikelihood`(sample, u)	Estimate the distribution with the profile likelihood.
`buildMethodOfXiProfileLikelihoodEstimator`(...)	Estimate the distribution and the parameter distribution with the profile likelihood.
`buildReturnLevelEstimator`(result, sample, m)	Estimate a return level and its distribution from the GPD parameters.
`buildReturnLevelProfileLikelihood`(sample, u, m)	Estimate a return level and its distribution with the profile likelihood.
`buildReturnLevelProfileLikelihoodEstimator`(...)	Estimate $(z_m, \xi)$ and its distribution with the profile likelihood.
`buildTimeVarying`(*args)	Estimate a non stationary GPD from a time-dependent parametric model.
`drawMeanResidualLife`(sample)	Draw the mean residual life plot.
`drawParameterThresholdStability`(sample, ...)	Draw the parameter threshold stability plot.
`getBootstrapSize`()	Accessor to the bootstrap size.
`getClassName`()	Accessor to the object's name.
`getKnownParameterIndices`()	Accessor to the known parameters indices.
`getKnownParameterValues`()	Accessor to the known parameters values.
`getName`()	Accessor to the object's name.
`getOptimizationAlgorithm`()	Accessor to the solver.
`hasName`()	Test if the object is named.
`setBootstrapSize`(bootstrapSize)	Accessor to the bootstrap size.
`setKnownParameter`(values, positions)	Accessor to the known parameters.
`setName`(name)	Accessor to the object's name.
`setOptimizationAlgorithm`(solver)	Accessor to the solver.

See also

DistributionFactory, GeneralizedPareto

Notes

The following ResourceMap entries can be used to tweak the parameters of the optimization solver involved in the different estimators:

GeneralizedParetoFactory-DefaultOptimizationAlgorithm
GeneralizedParetoFactory-MaximumEvaluationNumber
GeneralizedParetoFactory-MaximumAbsoluteError
GeneralizedParetoFactory-MaximumRelativeError
GeneralizedParetoFactory-MaximumObjectiveError
GeneralizedParetoFactory-MaximumConstraintError
GeneralizedParetoFactory-InitializationMethod
GeneralizedParetoFactory-NormalizationMethod

__init__(*args)¶

build(*args)¶

Build the distribution.

Available usages:

build()

build(sample)

build(param)

Parameters:

sample2-d sequence of float, of dimension 1: The sample from which $\vect{\theta} = (\sigma, \xi, u)$ are estimated.
paramsequence of float: The parameters of the GeneralizedPareto.

Returns:

distDistribution: The estimated GPD.

Notes

In the first usage, the default GeneralizedPareto distribution is built.

In the second usage, the chosen algorithm depends on the size of the sample compared to the ResourceMap key GeneralizedParetoFactory-SmallSize (see [matthys2003] for the theory):

If the sample size is less or equal to GeneralizedParetoFactory-SmallSize from ResourceMap, then the method of probability weighted moments is used. If it fails, the method of exponential regression is used.
Otherwise, the first method tried is the method of exponential regression, then the method of probability weighted moments if the first one fails.

In the third usage, a GeneralizedPareto distribution corresponding to the given parameters is built.

buildAsGeneralizedPareto(*args)¶

Build the distribution as a GeneralizedPareto type.

Available usages:

build()

build(sample)

build(param)

Parameters:

sample2-d sequence of float, of dimension 1: The sample from which $\vect{\theta} = (\sigma, \xi, u)$ are estimated.
paramsequence of float,: A vector of parameters of the GeneralizedPareto.

Returns:

distGeneralizedPareto

The estimated GPD as a GeneralizedPareto.

In the first usage, the default GeneralizedPareto distribution is built.

Notes

The strategy described in build() is followed.

buildCovariates(*args)¶

Estimate a GPD from covariates.

Parameters:

sample2-d sequence of float

Sample drawn from a GPD.

ufloat

The threshold.

covariates2-d sequence of float

Covariates sample. A constant column is automatically added if none is not provided.

sigmaIndicessequence of int, optional

Indices of covariates considered for parameter $\sigma$ .

By default, an empty sequence.

The index of the constant covariate is added if empty or if the covariates do not initially contain a constant column.

xiIndicessequence of int, optional

Indices of covariates considered for parameter $\xi$ .

By default, an empty sequence.

The index of the constant covariate is added if empty or if the covariates do not initially contain a constant column.

sigmaLinkFunction, optional

The $h_{\sigma}$ function.

By default, the identity function.

xiLinkFunction, optional

The $h_{\xi}$ function.

By default, the identity function.

initializationMethodstr, optional

The initialization method for the optimization problem: Generic or Static.

By default, the method Generic (see ResourceMap, key GeneralizedParetoFactory-InitializationMethod).

normalizationMethodstr, optional

The data normalization method: CenterReduce, MinMax or None.

By default, the method MinMax (see ResourceMap, key GeneralizedParetoFactory-NormalizationMethod).

Returns:

resultCovariatesResult: The result class.

Notes

Let $Z_{\vect{y}}$ whose excesses above the threshold $u$ follow a GPD whose parameters $(\sigma, \xi)$ depend on $d$ covariates denoted by $\vect{y} = \Tr{(y_1, \dots, y_d)}$ :

$Z_{\vect{y}} \sim \mbox{GPD}(\sigma(\vect{y}), \xi(\vect{y}), u)$

We assume that the threshold $u$ is known.

We denote by $(z_{\vect{y}_1}, \dots, z_{\vect{y}_n})$ the values of $Z_{\vect{y}}$ associated to the values of the covariates $(\vect{y}_1, \dots, \vect{y}_n)$ .

For numerical reasons, it is recommended to normalize the covariates. Each covariate $y_k$ has its own normalization:

$\tilde{y}_k = \tau_k(y_k) = \dfrac{y_k-c_k}{d_k}$

and with three ways of defining $(c_k,d_k)$ of the covariate $y_k$ :

the CenterReduce method where $c_k = \dfrac{1}{n} \sum_{i=1}^n y_{k,i}$ is the covariate mean and $d_k = \sqrt{\dfrac{1}{n} \sum_{i=1}^n (y_{k,i}-c_k)^2}$ is the standard deviation of the covariates;
the MinMax method where $c_k = \min_i y_{k,i}$ is the min value of the covariate $y_k$ and $d_k = \max_i y_{k,i}- \min_i y_{k,i}$ its range. This is the default method. This is the default method;
the None method where $c_k = 0$ and $d_k = 1$ : in that case, data are not normalized.

Let $\vect{\theta} = (\sigma, \xi)$ be the vector of parameters. Then, $\vect{\theta}$ depends on all the $d$ covariates even if each component of $\vect{\theta}$ only depends on a subset of the covariates. We denote by $(y_1^q, \dots, y_{d_q}^q)$ the $d_q$ covariates involved in the modelling of the component $\theta_q$ .

Each component $\theta_q$ can be written as a function of the normalized covariates:

$\theta_q(y_1^q, \dots, y_{d_q}^q) & = h_q\left(\sum_{i=1}^{d_q} \tilde{\beta}_i^q\tilde{y}_i^q \right)$

This relation can be written as a function of the real covariates:

$\theta_q(y_1^q, \dots, y_{d_q}^q) & = h_q\left(\sum_{i=1}^{d_q} \beta_i^qy_i^q + \beta_{d_q+1}^q \right)$

where:

$h_q: \Rset \mapsto \Rset$ is usually referred to as the inverse-link function of the component $\theta_q$ ,
each $\beta_i^{q} \in \Rset$ .

To allow some parameters to remain constant, i.e. independent of the covariates (this will generally be the case for the parameter $\xi$ ), the library systematically adds the constant covariate to the speciﬁed covariates.

The complete vector of parameters is defined by:

$\Tr{\vect{b}} & = \Tr{( \Tr{\vect{b}_1}, \dots, \Tr{\vect{b}_p} )} \in \Rset^{d_t}\\ \Tr{\vect{b}_q} & = (\beta_1^q, \dots, \beta_{d_q}^q)\in \Rset^{d_q}$

where $d_t = \sum_{q=1}^p d_q$ .

The estimator of $\vect{\beta}$ maximizes the likelihood of the model which is defined by:

$L(\vect{\beta}) = \prod_{i=1}^{n} g(z_{\vect{y}_i};\vect{\theta}(\vect{y}_i)))$

where $g(z_{\vect{y}_i};\vect{\theta}(\vect{y}_i))$ denotes the GPD density function with parameters $\vect{\theta}(\vect{y}_i)$ and evaluated at $z_{\vect{y}_i}$ .

Then, if none of the $\xi(\vect{y}_i)$ is zero, the log-likelihood is defined by:

$\ell (\vect{\beta}) = -\sum_{i=1}^{n} \left\{ \log(\sigma(\vect{y}_i)) + (1 + 1 / \xi(\vect{y}_i) ) \log\left[ 1+\xi(\vect{y}_i) \left( \frac{z_{\vect{y}_i} - \mu(\vect{y}_i)}{\sigma(\vect{y}_i)}\right) \right] + \left[ 1 + \xi(\vect{y}_i) \left( \frac{z_{\vect{y}_i}- \mu(\vect{y}_i)}{\sigma(\vect{y}_i)} \right) \right]^{-1 / \xi(\vect{y}_i)} \right\}$

defined on $(\mu, \sigma, \xi)$ such that $1+\xi \left( \frac{z_{\vect{y}_i} - \mu(\vect{y}_i)}{\sigma(\vect{y}_i)}\right) > 0$ for all $\vect{y}_i$ .

And if any of the $\xi(\vect{y}_i)$ is equal to 0, the log-likelihood is defined as:

$\ell (\vect{\beta}) = -\sum_{i=1}^{n} \left\{ \log(\sigma(\vect{y}_i)) + \frac{z_{\vect{y}_i} - \mu(\vect{y}_i)}{\sigma(\vect{y}_i)} + \exp \left\{ - \frac{z_{\vect{y}_i} - \mu(\vect{y}_i)}{\sigma(\vect{y}_i)} \right\} \right\}$

The initialization of the optimization problem is crucial. Two initial points $(\mu_0, \sigma_0, \xi_0)$ are proposed:

the Generic initial point: in that case, we assume that the GPD is stationary and $(\sigma_0, \xi_0)$ is the estimate resulting from the method buildAsGeneralizedPareto() which follows the strategy described in the method build(). This is the default initial point;
the Static initial point: in that case, we still assume that the GPD is stationary and $(\sigma_0, \xi_0)$ is the maximum likelihood estimate.

The result class provides:

the estimator $\hat{\vect{\beta}}$ ,
the asymptotic distribution of $\hat{\vect{\beta}}$ ,
the parameter function $(\vect{\beta}, \vect{y}) \mapsto \vect{\theta}(\vect{\beta}, \vect{y})$ ,
the graphs of the parameter functions $y_k \mapsto \theta_q(\vect{y})$ , where all the components of $\vect{y}$ are fixed to a reference value excepted for $y_k$ , for each $k$ ,
the graphs of the parameter functions $(y_k, y_\ell) \mapsto \theta_q(\vect{y})$ , where all the components of $\vect{y}$ are fixed to a reference value excepted for $(y_k, y_\ell)$ , for each $(k,\ell)$ ,
the normalizing function $\vect{y} \mapsto (\tau_1(y_1), \dots, \tau_d(y_d))$ ,
the optimal log-likelihood value $\hat{\vect{\beta}}$ ,
the GEV distribution at covariate $\vect{y}$ ,
the graphs of the quantile functions of order $p$ : $y_k \mapsto q_p(Z_{\vect{y}})$ where all the components of $\vect{y}$ are fixed to a reference value excepted for $y_k$ , for each $k$ ,
the graphs of the quantile functions of order $p$ : $(y_k, y_\ell) \mapsto q_p(Z_{\vect{y}})$ where all the components of $\vect{y}$ are fixed to a reference value excepted for $(y_k, y_\ell)$ , for each $(k,\ell)$ .

buildEstimator(*args)¶

Build the distribution and the parameter distribution.

Parameters:

sample2-d sequence of float: Data.
parametersDistributionParameters: Optional, the parametrization.

Returns:

resDistDistributionFactoryResult: The results.

Notes

According to the way the native parameters of the distribution are estimated, the parameters distribution differs:

Moments method: the asymptotic parameters distribution is normal and estimated by Bootstrap on the initial data;

Maximum likelihood method with a regular model: the asymptotic parameters distribution is normal and its covariance matrix is the inverse Fisher information matrix;

Other methods: the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting (see KernelSmoothing).

If another set of parameters is specified, the native parameters distribution is first estimated and the new distribution is determined from it:

if the native parameters distribution is normal and the transformation regular at the estimated parameters values: the asymptotic parameters distribution is normal and its covariance matrix determined from the inverse Fisher information matrix of the native parameters and the transformation;

in the other cases, the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting.

buildMethodOfExponentialRegression(sample)¶

Build the distribution based on the exponential regression estimator.

Parameters:

sample2-d sequence of float, of dimension 1: The sample from which $\vect{\theta} = (\sigma, \xi, u)$ are estimated.

Returns:

distGeneralizedPareto: The estimated GPD.

Notes

Lets denote:

$y_{i}=i\log\left(\dfrac{x_{(n-i)}-x_{(1)}}{x_{(n-i-1)}-x_{(1)}}\right)$ for $i\in\{1,n-3\}$

Then we estimate $(\hat{\sigma}, \hat{\xi}, \hat{u})$ using:

(1)¶ $\hat{\xi} & = \xi^* \\ \hat{\sigma} & = \dfrac{2(\overline{x}_n- \hat{u}_n)}{1-2\rho} \\ \hat{u} & = x_{(1)} - \frac{x_{(1)}}{2 + n}$

Where $\xi^*$ maximizes:

(2)¶ $\sum_{i=1}^{n-2}\log\left(\dfrac{1-(j/n)^{\xi}}{\xi}\right)-\dfrac{1-(j/n)^{\xi}}{\xi}y_i$

under the constraint $-1 \leq \xi \leq 1$ .

buildMethodOfLikelihoodMaximization(sample, u)¶

Estimate the distribution with the maximum likelihood method.

Parameters:

sample2-d sequence of float: Sample drawn from $X$ .
ufloat: Given threshold value.

Returns:

distributionGeneralizedExtremeValue: The estimated distribution of $(\hat{\sigma}, \hat{\xi})$ .

Notes

Let $X$ be a random variable whose excesses above $u$ follow a GPD parameterized by $\vect{\theta} = (\sigma, \xi)$ . We assume that $u$ is known.

Let $(x_1, \dots, x_n)$ be a sample drawn from $X$ . We define the excesses above $u$ by:

z_i = x_i - u

for all $1 \leq i \leq n$ .

The maximum likelihood estimator of $(\sigma, \xi)$ maximizes the log-likelihood defined by:

If $\xi \neq 0$ :

(3)¶ $\ell(\sigma, \xi) = -n \log \sigma - \sum_{i=1}^n \log \left(1 + \xi \frac{z_i}{\sigma}\right)$

defined on $(\sigma, \xi)$ such that $1+\xi \left( \frac{z_i - u}{\sigma} \right) > 0$ for all $1 \leq i \leq n$ .

If $\xi = 0$ :

(4)¶ $\ell(\sigma, \xi) = -n \log \sigma - \sigma^{-1} \sum_{i=1}^n \exp z_i$

buildMethodOfLikelihoodMaximizationEstimator(sample, u)¶

Estimate the distribution and the parameter distribution with the maximum likelihood method.

Parameters:

sample2-d sequence of float: Sample drawn from $X$ .
ufloat: Given threshold value.

Returns:

resultDistributionFactoryLikelihoodResult: The result class.

Notes

Let $X$ be a random variable whose excesses above $u$ follow a GPD parameterized by $\vect{\theta} = (\sigma, \xi)$ . We assume that $u$ is known.

The estimator $(\hat{\sigma}, \hat{\xi})$ is defined using the profile log-likelihood as detailed in buildMethodOfLikelihoodMaximization().

The result class produced by the method provides:

the GPD distribution associated to $(\hat{\sigma}, \hat{\xi}, u)$ ,
the asymptotic distribution of $(\hat{\sigma}, \hat{\xi}, u)$ .

buildMethodOfMoments(sample)¶

Build the distribution based on the method of moments estimator.

Parameters:

sample2-d sequence of float, of dimension 1: The sample from which $\vect{\theta} = (\sigma, \xi, u)$ are estimated.

Returns:

distGeneralizedPareto: The estimated GPD.

Notes

Lets denote:

$\displaystyle \overline{x}_n = \frac{1}{n} \sum_{i=1}^n x_i$ the empirical mean of the sample,
$\displaystyle s_n^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline{x}_n)^2$ its empirical variance.

Then, we estimate $(\hat{\sigma}_n, \hat{\xi}_n, \hat{u}_n)$ using:

(5)¶ $\hat{u}_n & = x_{(1)} - \dfrac{x_{(1)}}{2 + n} \\ \hat{\xi}_n & = -\dfrac{1}{2}\left(\dfrac{(\overline{x}_n - \hat{u}_n)^2}{s_n^2}-1\right) \\ \hat{\sigma}_n & = \dfrac{(\overline{x}_n- \hat{u}_n)}{2}\left(\dfrac{(\overline{x}_n- \hat{u}_n)^2}{s_n^2}+1\right)$

This estimator is well-defined only if $\hat{\xi}>-1/4$ , otherwise the second moment does not exist.

buildMethodOfProbabilityWeightedMoments(sample)¶

Build the distribution based on the probability weighted moments estimator.

Parameters:

sample2-d sequence of float, of dimension 1: The sample from which $\vect{\theta} = (\sigma, \xi, u)$ are estimated.

Returns:

distGeneralizedPareto: The estimated GPD.

Notes

Lets denote:

$\left(x_{(i)}\right)_{i\in\{1,\dots,n\}}$ the sample sorted in ascending order
$m=\dfrac{1}{n}\sum_{i=1}^n\left(1-\dfrac{i-7/20}{n}\right)x_{(i)}$
$\rho=\dfrac{m}{\overline{x}_n}$

Then we estimate $(\hat{\sigma}, \hat{\xi}, \hat{u})$ using:

(6)¶ $\hat{u}_n & = x_{(1)} - \frac{x_{(1)}}{2 + n}\\ \hat{\xi}_n & = \dfrac{1-4\rho}{1-2\rho} \\ \hat{\sigma}_n & = \dfrac{2(\overline{x}_n- \hat{u}_n)}{1-2\rho}$

This estimator is well-defined only if $\hat{\xi}_n>-1/2$ , otherwise the first moment does not exist.

buildMethodOfXiProfileLikelihood(sample, u)¶

Estimate the distribution with the profile likelihood.

Parameters:

sample2-d sequence of float: Sample drawn from $X$ .
ufloat: Given threshold value.

Returns:

distributionGeneralizedPareto: The estimated GPD.

Notes

Let $X$ be a random variable whose excesses above $u$ follow a GPD parameterized by $\vect{\theta} = (\sigma, \xi)$ . We assume that $u$ is known.

The estimator $(\hat{\sigma}, \hat{\xi})$ is defined using a nested numerical optimization of the log-likelihood:

$\ell_p (\xi) = \max_{(\sigma)} \ell (\sigma, \xi, u)$

where $\ell (\sigma, \xi, u)$ is detailed in equations (3) and (4).

The estimator is given by:

$\hat{\xi} & = \argmax_{\xi} \ell_p(\xi)\\ \hat{\sigma} & = \argmax_{\sigma} \ell(\sigma, \hat{\xi}, u)$

buildMethodOfXiProfileLikelihoodEstimator(sample, u)¶

Estimate the distribution and the parameter distribution with the profile likelihood.

Parameters:

sample2-d sequence of float: Sample drawn from $X$ .
ufloat: Given threshold value.

Returns:

resultProfileLikelihoodResult: The result class.

Notes

Let $X$ be a random variable whose excesses above $u$ follow a GPD parameterized by $\vect{\theta} = (\sigma, \xi)$ . We assume that $u$ is known.

The estimator $(\hat{\sigma}, \hat{\xi})$ is defined in buildMethodOfXiProfileLikelihood().

The result class produced by the method provides:

the GPD distribution associated to $(\hat{\sigma}, \hat{\xi}, u)$ ,
the asymptotic distribution of $(\hat{\sigma}, \hat{\xi}, u)$ ,
the profile log-likelihood function $\xi \mapsto \ell_p(\xi)$ ,
the optimal profile log-likelihood value $\ell_p(\hat{\xi})$ ,
confidence intervals of level $(1-\alpha)$ of $\xi$ .

buildReturnLevelEstimator(result, sample, m, theta=1.0)¶

Estimate a return level and its distribution from the GPD parameters.

Parameters:

resultDistributionFactoryResult

Likelihood estimation result obtained to estimate the GPD $(\sigma, \xi, u)$ .

sample2-d sequence of float

The initial data from which the clusters (if any) have been extracted. If the data are independent, sample is the sample used to get result.

mfloat

The return period expressed in terms of number of observations.

thetafloat, optional

The extremal index defined in (9).

Default value is 1.

Returns:

distributionDistribution: The asymptotic distribution of $\hat{z}_m$ .

Notes

Let $Z$ a random variable whose excesses above the threshold $u$ follow a Generalized Pareto distribution $GPD(\sigma, \xi)$ . We assume that $u$ is known.

The $m$ -observation return level $z_m$ is the level exceeded on average once every $m$ observations. The $m$ -observation return level can be translated into the annual-scale: if there are $n_y$ observations per year, then the $N$ -year return level corresponds to the $m$ -observation return level where $m = n_yN$ .

The $m$ -observation return level is defined as a particular quantile of $Z$ :

If $\xi \neq 0$ :

(7)¶ $z_m = u + \frac{\sigma}{\xi}\left[(m \zeta_u \theta)^{\xi} - 1 \right]$

If $\xi = 0$ :

(8)¶ $z_m = u + \sigma \log(m \zeta_u \theta)$

with $\zeta_u$ the probability of an exceedance of $u$ and $\theta$ the extremal index. Denoting the number of observations by $n$ , the number of exceedances of the threshold $u$ by $n_u$ and the number of clusters obtained above $u$ by $n_c$ , then $\zeta_u$ and $\theta$ are estimated by:

(9)¶ $\zeta_u & = \dfrac{n_u}{n}\\ \theta & = \dfrac{n_c}{n_u}$

If the data are independent, no clustering is performed and $\theta=1$ .

The estimator $\hat{z}_m$ of $z_m$ is deduced from the estimator $(\hat{\sigma}, \hat{\xi}, \hat{\zeta_u})$ of $(\sigma, \xi, \zeta_u)$ of the GPD.

The asymptotic distribution of $\hat{z}_m$ is obtained by the Delta method from the asymptotic distribution of $(\hat{\sigma}, \hat{\xi}, \hat{\zeta}_u)$ . It is a normal distribution with mean $\hat{z}_m$ and variance:

$\Var{\hat{z}_m} = (\nabla z_m)^T \mat{V}_n \nabla z_m$

where $\nabla z_m = (\frac{\partial z_m}{\partial \mu}, \frac{\partial z_m}{\partial \sigma}, \frac{\partial z_m}{\partial \xi})$ and $\mat{V}_n$ is the asymptotic covariance of $(\hat{\sigma}, \hat{\xi}, \hat{\mu})$ .

buildReturnLevelProfileLikelihood(sample, u, m, theta=1.0)¶

Estimate a return level and its distribution with the profile likelihood.

Parameters:

sample2-d sequence of float

A sample of dimension 1.

ufloat

The threshold.

mfloat

The return period expressed in terms of number of observations.

thetafloat, optional

The extremal index defined in (9).

Default value is 1.

Returns:

distributionNormal: The asymptotic distribution of $\hat{z}_m$ .

Notes

Let $Z$ a random variable whose excesses above the threshold $u$ follow a Generalized Pareto distribution $GPD(\sigma, \xi)$ . We assume that $u$ is known.

The return level $z_m$ is defined in buildReturnLevelEstimator().

The estimator $\hat{z}_m$ of $z_m$ is defined using a nested numerical optimization of the log-likelihood:

$\ell_p (z_m) = \max_{\xi} \ell (z_m, \xi, u)$

where $\ell (z_m, \xi, u)$ is the log-likelihood detailed in (3) and (4) where we substitued $\sigma$ for $z_m$ using equations (7) or (8).

Then $\hat{z}_m$ is defined by:

$\hat{z}_m = \argmax_{z_m} \ell_p(z_m)$

The asymptotic distribution of $\hat{z}_m$ is normal.

The starting point of the optimization is initialized from the regular maximum likelihood method.

buildReturnLevelProfileLikelihoodEstimator(sample, u, m, theta=1.0)¶

Estimate $(z_m, \xi)$ and its distribution with the profile likelihood.

Parameters:

sample2-d sequence of float: A sample of dimension 1.
ufloat: The threshold.
mfloat: The return period expressed in terms of number of observations.
thetafloat, optional: When clustering is performed, this is the ratio $\theta = \frac{n_c}{n_u}$ of number of clusters over number of exceedances, otherwise defaults to 1.

Returns:

resultProfileLikelihoodResult: The result class.

Notes

Let $Z$ a random variable whose excesses above the threshold $u$ follow a Generalized Pareto distribution $GPD(\sigma, \xi)$ . We assume that $u$ is known.

The return level $z_m$ is defined in buildReturnLevelEstimator(). The profile log-likelihood $\ell_p(z_m)$ is defined in buildReturnLevelProfileLikelihood().

The result class produced by the method provides:

the GPD distribution associated to $(\hat{z}_m, \hat{\xi}, u)$ ,
the asymptotic distribution of $(\hat{z}_m, \hat{\xi}, u)$ ,
the profile log-likelihood function $z_m \mapsto \ell_p(z_m)$ ,
the optimal profile log-likelihood value $\ell_p(\hat{z}_m)$ ,
confidence intervals of level $(1-\alpha)$ of $\hat{z}_m$ .

buildTimeVarying(*args)¶

Estimate a non stationary GPD from a time-dependent parametric model.

Parameters:

sample2-d sequence of float

Sample drawn from $Z_t$ .

ufloat

The threshold.

timeStamps2-d sequence of float

Values of $t$ .

basisBasis

Functional basis.

sigmaIndicessequence of int, optional

Indices of basis terms considered for parameter $\sigma$ .

xiIndicessequence of int, optional

Indices of basis terms considered for parameter $\xi$ .

sigmaLinkFunction, optional

The $h_{\sigma}$ function.

By default, the identity function.

xiLinkFunction, optional

The $h_{\xi}$ function.

By default, the identity function.

initializationMethodstr, optional

The initialization method for the optimization problem: Generic or Static.

By default, the method Generic (see ResourceMap, key GeneralizedParetoFactory-InitializationMethod).

normalizationMethodstr, optional

The data normalization method: CenterReduce, MinMax or None.

By default, the method MinMax (see ResourceMap, key GeneralizedParetoFactory-NormalizationMethod).

Returns:

resultTimeVaryingResult: The result class.

Notes

Let $Z_t$ be a non stationary random variable whose excesses above the threshold $u$ follow a GPD. We assume that $u$ is known:

$Z_t \sim \mbox{GPD}(\sigma(t), \xi(t), u)$

We denote by $(z_{t_1}, \dots, z_{t_n})$ the values of $Z_t$ on the time stamps $(t_1, \dots, t_n)$ .

For numerical reasons, it is recommended to normalize the time stamps. The following mapping is applied:

$\tau(t) = \dfrac{t-c}{d}$

and with three ways of defining $(c,d)$ :

the CenterReduce method where $c = \dfrac{1}{n} \sum_{i=1}^n t_i$ is the mean time stamps and $d = \sqrt{\dfrac{1}{n} \sum_{i=1}^n (t_i-c)^2}$ is the standard deviation of the time stamps;
the MinMax method where $c = t_1$ is the first time and $d = t_n-t_1$ the range of the time stamps. This is the default method;
the None method where $c = 0$ and $d = 1$ : in that case, data are not normalized.

If we denote by $\theta_q$ is a component of $\vect{\theta} = (\sigma, \xi)$ , then $\theta_q$ can be written as a function of $t$ :

$\theta_q(t) = h_q\left(\sum_{i=1}^{d_{\theta_q}} \beta_i^{\theta_q} \varphi_i^{\theta_q} (\tau(t))\right)$

where:

$d_{\theta_q}$ is the size of the functional basis involved in the modelling of $\theta_q$ ,
$h_q: \Rset \mapsto \Rset$ is usually referred to as the inverse-link function of the parameter $\theta_q$ ,
each $\varphi_i^{\theta_q}$ is a scalar function $\Rset \mapsto \Rset$ ,
each $\beta_i^{j} \in \Rset$ .

We denote by $d_{\sigma}$ and $d_{\xi}$ the size of the functional basis of $\sigma$ and $\xi$ respectively. We denote by $\vect{\beta} = (\beta_1^{\sigma}, \dots, \beta_{d_{\sigma}}^{\sigma}, \beta_1^{\xi}, \dots, \beta_{d_{\xi}}^{\xi})$ the complete vector of parameters.

The estimator of $\vect{\beta}$ maximizes the likelihood of the non stationary model which is defined by:

$L(\vect{\beta}) = \prod_{i=1}^{n} g(z_{t_i};\sigma(t_i), \xi(t_i), u)$

where $g(z_{t};\sigma(t), \xi(t))$ denotes the GPD density function with parameters $(\sigma(t), \xi(t), u)$ evaluated at $z_t$ .

Then, if none of the $\xi(t)$ is zero, the log-likelihood is defined by:

$\ell (\vect{\beta}) = -\sum_{i=1}^{n} \left\{ \log(\sigma(t_i)) + (1 + 1 / \xi(t_i) ) \log\left[ 1+\xi(t_i) \left( \frac{z_{t_i} - \mu(t_i)}{\sigma(t_i)}\right) \right] + \left[ 1 + \xi(t_i) \left( \frac{z_{t_i}- \mu(t_i)}{\sigma(t_i)} \right) \right]^{-1 / \xi(t_i)} \right\}$

defined on $(\sigma, \xi, u)$ such that $1+\xi(t) \left( \frac{z_t - \mu(t)}{\sigma(t)} \right) > 0$ for all $t$ .

And if any of the $\xi(t_i)$ is equal to 0, the log-likelihood is defined as:

$\ell (\vect{\beta}) = -\sum_{i=1}^{n} \left\{ \log(\sigma(t_i)) + \frac{z_{t_i} - \mu(t_i)} {\sigma(t_i)} + \exp \left\{ - \frac{z_{t_i} - \mu(t_i)}{\sigma(t_i)} \right\} \right\}$

The initialization of the optimization problem is crucial. Two initial points $(\mu_0, \sigma_0, \xi_0)$ are proposed:

the Generic initial point: in that case, we assume that the GPD is stationary and $(\sigma_0, \xi_0)$ is the estimate resulting from the method buildAsGeneralizedPareto() which follows the strategy described in the method build(). This is the default initial point;
the Static initial point: in that case, we still assume that the GPD is stationary and $(\sigma_0, \xi_0)$ is the maximum likelihood estimate.

The result class produced by the method provides:

the estimator $\hat{\vect{\beta}}$ ,
the asymptotic distribution of $\hat{\vect{\beta}}$ ,
the parameter functions $t \mapsto \vect{\theta}(t)$ ,
the normalizing function $t \mapsto \tau(t)$ ,
the optimal log-likelihood value $\hat{\vect{\beta}}$ ,
the GPD distribution at time $t$ ,
the quantile functions of order $p$ : $t \mapsto q_p(Z_t)$ .

drawMeanResidualLife(sample)¶

Draw the mean residual life plot.

Parameters:

sample2-d sequence of float, of dimension 1: The sample drawn from $X$ .

Returns:

graphGraph: The graph of $u \mapsto m_n(u)$ and its $95\%$ confidence interval.

Notes

This method is complementary to drawParameterThresholdStability() as a method of threshold selection.

Let $X$ a random variable defined whose excesses above the threshold $u_0$ follow the Generalized Pareto distribution $GPD(\xi, \sigma_0)$ . The mean of excesses of $X$ for $u > u_0$ is

$\Expect{X-u|X>u} = \frac{\sigma_0+\xi u}{1-\xi}$

Hence, for all $u>u_0$ $\Expect{X-u|X>u}$ is a linear function of $u$ . The threshold $u_0$ is the smallest value of $u$ from which the curve is linear.

The quantity $\Expect{X-u|X>u}$ is estimated by the empirical estimator of the mean:

$M_n(u) = \frac{1}{n} \sum_{i=1}^n (X_i - u) 1_{X_i \ge u} = \frac{1}{n} \sum_{i=1}^n X_i 1_{X_i \ge u} - u$

The estimator $M_n(u)$ is asymptotically normal with mean $\mu(u) = \Expect{X-u|X>u}$ and variance $\mu(u)(1 - \mu(u))/n$ .

We denote by $m_n(u)$ its realization on the sample drawn from $X$ . The mean and the variance of $M_n(u)$ are respectively estimated by $m_n(u)$ and $m_n(u)(1-m_n(u))$ .

The graph $u \mapsto m_n(u)$ is termed the mean residual life plot.

The confidence level can be set using the ResourceMap key GeneralizedParetoFactory-MeanResidualLifeConfidenceLevel The number of threshold points in the graph can be set with the key GeneralizedParetoFactory-MeanResidualLifePointNumber.

drawParameterThresholdStability(sample, thresholdRange)¶

Draw the parameter threshold stability plot.

Parameters:

sample2-d sequence of float, of dimension 1: The sample drawn from $X$ .
uRangeInterval: The range of the threshold $u: [u_{min}, u_{max}]$ .

Returns:

graphGraph: The graphs of $u \mapsto \hat{\sigma}^{\ast}$ and $u \mapsto \hat{\xi}$ .

Notes

This method is complementary to drawMeanResidualLife() as a method of threshold selection.

Let $X$ a random variable whose excesses above the threshold $u_0$ follow a Generalized Pareto distribution $GPD(\sigma_0, \xi)$ . Then the excesses of $X$ above $u>u_0$ also follow a Generalized Pareto distribution $GPD( \sigma_u, \xi)$ where:

(10)¶ $\sigma_u = \sigma_0 + \xi (u - u_0)$

Hence, if we define the modified scale parameter $\sigma^{\ast}$ by:

$\sigma^{\ast} = \sigma_u - \xi u$

then , by virtue of (10), $\sigma^{\ast}$ is constant with respect to $u$ .

Consequently, estimates of $\sigma^{\ast}$ and $\xi$ should be constant (or stable accounting for sampling variability) above $u_0$ if $u_0$ is a valid threshold for excesses to follow a Generalized Pareto distribution.

The method draws the graphs of $u \mapsto \hat{\sigma}^{\ast}$ and $u \mapsto \hat{\xi}$ with the respective $95\%$ confidence intervals, for $u \in [u_{min}, u_{max}]$ . The selected threshold is the lowest value of $u$ from which the estimates remain near-constant.

The confidence level can be set using the ResourceMap key GeneralizedParetoFactory-ThresholdStabilityConfidenceLevel The number of threshold points in the graph can be set with the key GeneralizedParetoFactory-ThresholdStabilityPointNumber.

getBootstrapSize()¶

Accessor to the bootstrap size.

Returns:

sizeint: Size of the bootstrap.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getKnownParameterIndices()¶

Accessor to the known parameters indices.

Returns:

indicesIndices: Indices of the known parameters.

getKnownParameterValues()¶

Accessor to the known parameters values.

Returns:

valuesPoint: Values of known parameters.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOptimizationAlgorithm()¶

Accessor to the solver.

Returns:

solverOptimizationAlgorithm: The solver used for numerical optimization of the likelihood.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

setBootstrapSize(bootstrapSize)¶

Accessor to the bootstrap size.

Parameters:

sizeint: The size of the bootstrap.

setKnownParameter(values, positions)¶

Accessor to the known parameters.

Parameters:

valuessequence of float: Values of known parameters.
positionssequence of int: Indices of known parameters.

Examples

When a subset of the parameter vector is known, the other parameters only have to be estimated from data.

In the following example, we consider a sample and want to fit a Beta distribution. We assume that the $a$ and $b$ parameters are known beforehand. In this case, we set the third parameter (at index 2) to -1 and the fourth parameter (at index 3) to 1.

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> distribution = ot.Beta(2.3, 2.2, -1.0, 1.0)
>>> sample = distribution.getSample(10)
>>> factory = ot.BetaFactory()
>>> # set (a,b) out of (r, t, a, b)
>>> factory.setKnownParameter([-1.0, 1.0], [2, 3])
>>> inf_distribution = factory.build(sample)