Note

Go to the end to download the full example code.

Example 1: Axial stressed beamΒΆ

In this test case, we create a sample from a mixture and we try to estimate the mixture parameters from the sample. It is not a really an example of a study but it shows how to use this module. The optimal number of clusters is not supposed to be known, and will be estimated as well. We are in dimension 2, and the reference mixture is defined from 3 normal distributions:

f(x) = \alpha_1 f_1(x) + \alpha_2 f_2(x) + \alpha_3 f_3(x)

with:

  • f_1=N(\mu_1,\sigma_1,R_1) with \mu_1=(-2.2,-2.2), \sigma_1=(1.2,1.2), R_1=-0.2 and \alpha_1 = 0.5,

  • f_2=N(\mu_2,\sigma_2,R_2) with \mu_2=(2,2), \sigma_2=(0.8, 0.8), R_2=0.1 and \alpha_2 = 0.25,

  • f_3=N(\mu_3,\sigma_3,R_3) with \mu_3=(-5,5), \sigma_3=(1.4,1.4), R_3=0 and \alpha_3 = 0.25.

import openturns as ot
import openturns.viewer as otv
import otmixmod

Create a multidimensional sample from a mixture of Normal

dim = 2
size = 20000
coll = []
R = ot.CorrelationMatrix(dim)

First atom

for i in range(dim - 1):
    R[i, i + 1] = -0.2
mean = ot.Point(dim, -2.2)
sigma = ot.Point(dim, 1.2)
d = ot.Normal(mean, sigma, R)
coll.append(d)

Second atom

R = ot.CorrelationMatrix(dim)
for i in range(dim - 1):
    R[i, i + 1] = 0.1
mean = ot.Point(dim, 2.0)
sigma = ot.Point(dim, 0.8)
d = ot.Normal(mean, sigma, R)
coll.append(d)

Third atom

mean = [-5.0, 5.0]
sigma = [1.4] * 2
R = ot.CorrelationMatrix(dim)
d = ot.Normal(mean, sigma, R)
coll.append(d)

weights = [0.5, 0.25, 0.25]

Reference mixture

mixture = ot.Mixture(coll, weights)

Creation of the numerical Sample from which we will estimate the parameters of the mixture.

sample = mixture.getSample(size)

Creation of the mixture factory

myAtomsNumber = 3
myCovModel = 'Gaussian_pk_L_Dk_A_Dk'

bestLL = -1e100
bestMixture = ot.Mixture()
bestNbClusters = 0
stop = False
nbClusters = 1
while not stop:
    factory = otmixmod.MixtureFactory(nbClusters, myCovModel)
    # Estimation of the parameters of the mixture
    estimatedDistribution, labels, logLikelihood = factory.build(sample)
    stop = logLikelihood[1] <= bestLL
    if not stop:
        bestLL = logLikelihood[1]
        bestNbClusters = nbClusters
        bestMixture = estimatedDistribution
    nbClusters += 1
print("best number of atoms=", bestNbClusters)
myAtomsNumber = bestNbClusters
estimatedDistribution = bestMixture
# Some printings to show the result
print("Covariance Model used=", myCovModel)

print("")
print("Estimated distribution:", estimatedDistribution)

best number of atoms= 3
Covariance Model used= Gaussian_pk_L_Dk_A_Dk

Estimated distribution: Mixture((w = 0.254333, d = Normal(mu = [1.94368,1.98439], sigma = [1.21056,1.13791], R = [[ 1        0.119447 ]
 [ 0.119447 1        ]])), (w = 0.50104, d = Normal(mu = [-2.21622,-2.21449], sigma = [1.17175,1.17784], R = [[  1        -0.134189 ]
 [ -0.134189  1        ]])), (w = 0.244627, d = Normal(mu = [-5.03441,5.03529], sigma = [1.09358,1.25075], R = [[ 1         0.0148212 ]
 [ 0.0148212 1         ]])))

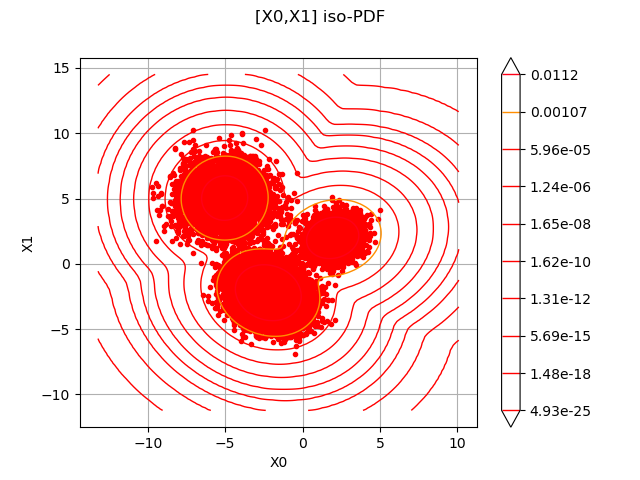
Some drawings

if sample.getDimension() == 2:
    g = estimatedDistribution.drawPDF()
    c = ot.Cloud(sample)
    c.setColor("red")
    c.setPointStyle("bullet")
    ctmp = g.getDrawable(0)
    g.setDrawable(c, 0)
    g.add(ctmp)
    view = otv.View(g)

otv.View.ShowAll()
[X0,X1] iso-PDF

Total running time of the script: (0 minutes 1.444 seconds)