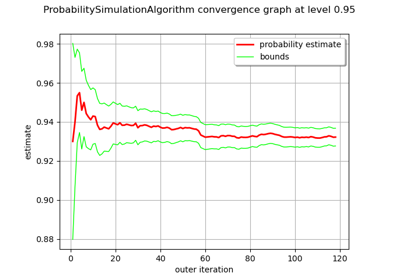
ProbabilitySimulationAlgorithm¶

class ProbabilitySimulationAlgorithm(*args)¶

Iterative sampling methods.

Refer to Monte Carlo simulation, Importance Simulation, Latin Hypercube Simulation, Quasi Monte Carlo.

Available constructor:

ProbabilitySimulationAlgorithm(event, experiment, verbose=True, convergenceStrategy=ot.Compact())

ProbabilitySimulationAlgorithm(event, verbose=True, convergenceStrategy=ot.Compact())

Parameters:

eventRandomVector: The event we are computing the probability of, must be composite.
experimentWeightedExperiment: Sequential experiment
verbosebool, optional: If True, make the computation verbose.
convergenceStrategyHistoryStrategy, optional: Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.

See also

EventSimulation

Notes

Using the probability distribution of a random vector $\vect{X}$ , we seek to evaluate the following probability:

$P_f = \Prob{g\left( \vect{X},\vect{d} \right) \leq 0}$

Here, $\vect{X}$ is a random vector, $\vect{d}$ a deterministic vector, $g(\vect{X},\vect{d})$ the function known as limit state function which enables the definition of the event

$\cD_f = \{\vect{X} \in \Rset^n \, | \, g(\vect{X},\vect{d}) \le 0\}$

If we have the set $\left\{ \vect{x}_1,\ldots,\vect{x}_N \right\}$ of $N$ independent samples of the random vector $\vect{X}$ , we can estimate $\widehat{P}_f$ as follows:

$\widehat{P}_{f,MC} = \frac{1}{N} \sum_{i=1}^N \mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} }$

where $\mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} }$ describes the indicator function equal to 1 if $g(\vect{x}_i,\vect{d}) \leq 0$ and equal to 0 otherwise; the idea here is in fact to estimate the required probability by the proportion of cases, among the $N$ samples of $\vect{X}$ , for which the event $\cD_f$ occurs.

By the law of large numbers, we know that this estimation converges to the required value $P_f$ as the sample size $N$ tends to infinity.

The Central Limit Theorem allows one to build an asymptotic confidence interval using the normal limit distribution as follows:

$\lim_{N\rightarrow\infty}\Prob{P_f\in[\widehat{P}_{f,\inf},\widehat{P}_{f,\sup}]}=\alpha$

with $\widehat{P}_{f,\inf}=\widehat{P}_f - q_{\alpha}\sqrt{\frac{\widehat{P}_f(1-\widehat{P}_f)}{N}}$ , $\widehat{P}_{f,\sup}=\widehat{P}_f + q_{\alpha}\sqrt{\frac{\widehat{P}_f(1-\widehat{P}_f)}{N}}$ and $q_\alpha$ is the $(1+\alpha)/2$ -quantile of the standard normal distribution.

A ProbabilitySimulationAlgorithm object makes sense with the following sequential experiments:

MonteCarloExperiment
ImportanceSamplingExperiment
LowDiscrepancyExperiment
LHSExperiment (for the non randomized version see LHS)

The estimator built by Monte Carlo method is:

$\widehat{P}_{f,MC} = \frac{1}{N} \sum_{i=1}^N \mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} }$

where $\mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} }$ describes the indicator function equal to 1 if $g(\vect{x}_i,\vect{d}) \leq 0$ and equal to 0 otherwise; the idea here is in fact to estimate the required probability by the proportion of cases, among the $N$ samples of $\vect{X}$ , for which the event $\cD_f$ occurs.

By the law of large numbers, we know that this estimation converges to the required value $P_f$ as the sample size $N$ tends to infinity.

The Central Limit Theorem allows one to build an asymptotic confidence interval using the normal limit distribution as follows:

$\lim_{N\rightarrow\infty}\Prob{P_f\in[\widehat{P}_{f,\inf},\widehat{P}_{f,\sup}]}=\alpha$

with $\widehat{P}_{f,\inf}=\widehat{P}_f - q_{\alpha}\sqrt{\frac{\widehat{P}_f(1-\widehat{P}_f)}{N}}$ , $\widehat{P}_{f,\sup}=\widehat{P}_f + q_{\alpha}\sqrt{\frac{\widehat{P}_f(1-\widehat{P}_f)}{N}}$ and $q_\alpha$ is the $(1+\alpha)/2$ -quantile of the standard normal distribution.

The estimator built by Importance Sampling method is:

$\widehat{P}_{f,IS} = \frac{1}{N} \sum_{i=1}^N \mathbf{1}_{\{g(\vect{Y}_{\:i}),\vect{d}) \leq 0 \}} \frac{f_{\uX}(\vect{Y}_{\:i})} {f_{\vect{Y}}(\vect{Y}_{\:i})}$

where:

$N$ is the total number of computations,
the random vectors $\{\vect{Y}_i, i=1\hdots N\}$ are independent, identically distributed and following the probability density function $f_{\uY}$ .

Examples

Estimate a probability by Monte Carlo

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myFunction = ot.SymbolicFunction(['E', 'F', 'L', 'I'], ['-F*L^3/(3*E*I)'])
>>> myDistribution = ot.Normal([50.0, 1.0, 10.0, 5.0], [1.0]*4, ot.IdentityMatrix(4))
>>> # We create a 'usual' RandomVector from the Distribution
>>> vect = ot.RandomVector(myDistribution)
>>> # We create a composite random vector
>>> output = ot.CompositeRandomVector(myFunction, vect)
>>> # We create an Event from this RandomVector
>>> event = ot.ThresholdEvent(output, ot.Less(), -3.0)
>>> # We create a Monte Carlo algorithm
>>> experiment = ot.MonteCarloExperiment()
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(150)
>>> algo.setBlockSize(4)
>>> algo.setMaximumCoefficientOfVariation(0.1)
>>> # Perform the simulation
>>> algo.run()
>>> print('Probability estimate=%.6f' % algo.getResult().getProbabilityEstimate())
Probability estimate=0.140000

Estimate a probability by Importance Sampling

>>> ot.RandomGenerator.SetSeed(0)
>>> # assume we obtained a design point from FORM
>>> standardSpaceDesignPoint = [-0.0310363,0.841879,0.445462,-0.332318]
>>> standardEvent = ot.StandardEvent(event)
>>> importanceDensity = ot.Normal(standardSpaceDesignPoint, ot.CovarianceMatrix(4))
>>> experiment = ot.ImportanceSamplingExperiment(importanceDensity)
>>> algo = ot.ProbabilitySimulationAlgorithm(standardEvent, experiment)
>>> algo.setMaximumOuterSampling(150)
>>> algo.setBlockSize(4)
>>> algo.setMaximumCoefficientOfVariation(0.1)
>>> # Perform the simulation
>>> algo.run()
>>> print('Probability estimate=%.6f' % algo.getResult().getProbabilityEstimate())
Probability estimate=0.153315

Estimate a probability by Quasi Monte Carlo

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LowDiscrepancyExperiment()
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(150)
>>> algo.setBlockSize(4)
>>> algo.setMaximumCoefficientOfVariation(0.1)
>>> # Perform the simulation
>>> algo.run()
>>> print('Probability estimate=%.6f' % algo.getResult().getProbabilityEstimate())
Probability estimate=0.141667

Estimate a probability by Randomized Quasi Monte Carlo

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LowDiscrepancyExperiment()
>>> experiment.setRandomize(True)
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(150)
>>> algo.setBlockSize(4)
>>> algo.setMaximumCoefficientOfVariation(0.1)
>>> # Perform the simulation
>>> algo.run()
>>> print('Probability estimate=%.6f' % algo.getResult().getProbabilityEstimate())
Probability estimate=0.160000

Estimate a probability by Randomized LHS

>>> ot.RandomGenerator.SetSeed(0)
>>> experiment = ot.LHSExperiment()
>>> experiment.setAlwaysShuffle(True)
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(150)
>>> algo.setBlockSize(4)
>>> algo.setMaximumCoefficientOfVariation(0.1)
>>> # Perform the simulation
>>> algo.run()
>>> print('Probability estimate=%.6f' % algo.getResult().getProbabilityEstimate())
Probability estimate=0.140000

Methods

`drawProbabilityConvergence`(*args)	Draw the probability convergence at a given level.
`getBlockSize`()	Accessor to the block size.
`getClassName`()	Accessor to the object's name.
`getConvergenceStrategy`()	Accessor to the convergence strategy.
`getEvent`()	Accessor to the event.
`getExperiment`()	Accessor to the experiment.
`getId`()	Accessor to the object's id.
`getMaximumCoefficientOfVariation`()	Accessor to the maximum coefficient of variation.
`getMaximumOuterSampling`()	Accessor to the maximum sample size.
`getMaximumStandardDeviation`()	Accessor to the maximum standard deviation.
`getName`()	Accessor to the object's name.
`getResult`()	Accessor to the results.
`getShadowedId`()	Accessor to the object's shadowed id.
`getVerbose`()	Accessor to verbosity.
`getVisibility`()	Accessor to the object's visibility state.
`hasName`()	Test if the object is named.
`hasVisibleName`()	Test if the object has a distinguishable name.
`run`()	Launch simulation.
`setBlockSize`(blockSize)	Accessor to the block size.
`setConvergenceStrategy`(convergenceStrategy)	Accessor to the convergence strategy.
`setExperiment`(experiment)	Accessor to the experiment.
`setMaximumCoefficientOfVariation`(...)	Accessor to the maximum coefficient of variation.
`setMaximumOuterSampling`(maximumOuterSampling)	Accessor to the maximum sample size.
`setMaximumStandardDeviation`(...)	Accessor to the maximum standard deviation.
`setName`(name)	Accessor to the object's name.
`setProgressCallback`(*args)	Set up a progress callback.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setStopCallback`(*args)	Set up a stop callback.
`setVerbose`(verbose)	Accessor to verbosity.
`setVisibility`(visible)	Accessor to the object's visibility state.

__init__(*args)¶

drawProbabilityConvergence(*args)¶

Draw the probability convergence at a given level.

Parameters:

levelfloat, optional: The probability convergence is drawn at this given confidence length level. By default level is 0.95.

Returns:

grapha Graph: probability convergence graph

getBlockSize()¶

Accessor to the block size.

Returns:

blockSizeint: Number of terms in the probability simulation estimator grouped together. It is set by default to 1.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getConvergenceStrategy()¶

Accessor to the convergence strategy.

Returns:

storage_strategyHistoryStrategy: Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.

getEvent()¶

Accessor to the event.

Returns:

eventRandomVector: Event we want to evaluate the probability.

getExperiment()¶

Accessor to the experiment.

Returns:

experimentWeightedExperiment: The experiment that is sampled at each iteration.

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getMaximumCoefficientOfVariation()¶

Accessor to the maximum coefficient of variation.

Returns:

coefficientfloat: Maximum coefficient of variation of the simulated sample.

getMaximumOuterSampling()¶

Accessor to the maximum sample size.

Returns:

outerSamplingint: Maximum number of groups of terms in the probability simulation estimator.

getMaximumStandardDeviation()¶

Accessor to the maximum standard deviation.

Returns:

sigmafloat, $\sigma > 0$: Maximum standard deviation of the estimator.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getResult()¶

Accessor to the results.

Returns:

resultsSimulationResult: Structure containing all the results obtained after simulation and created by the method run().

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getVerbose()¶

Accessor to verbosity.

Returns:

verbosity_enabledbool: If True, the computation is verbose. By default it is verbose.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

run()¶

Launch simulation.

See also

setBlockSize, setMaximumOuterSampling, ResourceMap, SimulationResult

Notes

It launches the simulation and creates a SimulationResult, structure containing all the results obtained after simulation. It computes the probability of occurrence of the given event by computing the empirical mean of a sample of size at most outerSampling * blockSize, this sample being built by blocks of size blockSize. It allows one to use efficiently the distribution of the computation as well as it allows one to deal with a sample size $> 2^{32}$ by a combination of blockSize and outerSampling.

setBlockSize(blockSize)¶

Accessor to the block size.

Parameters:

blockSizeint, $blockSize \geq 1$: Number of terms in the probability simulation estimator grouped together. It is set by default to 1.

Notes

For Monte Carlo, LHS and Importance Sampling methods, this allows one to save space while allowing multithreading, when available we recommend to use the number of available CPUs; for the Directional Sampling, we recommend to set it to 1.

setConvergenceStrategy(convergenceStrategy)¶

Accessor to the convergence strategy.

Parameters:

storage_strategyHistoryStrategy: Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.

setExperiment(experiment)¶

Accessor to the experiment.

Parameters:

experimentWeightedExperiment: The experiment that is sampled at each iteration.

setMaximumCoefficientOfVariation(maximumCoefficientOfVariation)¶

Accessor to the maximum coefficient of variation.

Parameters:

coefficientfloat: Maximum coefficient of variation of the simulated sample.

setMaximumOuterSampling(maximumOuterSampling)¶

Accessor to the maximum sample size.

Parameters:

outerSamplingint: Maximum number of groups of terms in the probability simulation estimator.

setMaximumStandardDeviation(maximumStandardDeviation)¶

Accessor to the maximum standard deviation.

Parameters:

sigmafloat, $\sigma > 0$: Maximum standard deviation of the estimator.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setProgressCallback(*args)¶

Set up a progress callback.

Can be used to programmatically report the progress of a simulation.

Parameters:

callbackcallable: Takes a float as argument as percentage of progress.

Examples

>>> import sys
>>> import openturns as ot
>>> experiment = ot.MonteCarloExperiment()
>>> X = ot.RandomVector(ot.Normal())
>>> Y = ot.CompositeRandomVector(ot.SymbolicFunction(['X'], ['1.1*X']), X)
>>> event = ot.ThresholdEvent(Y, ot.Less(), -2.0)
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(100)
>>> algo.setMaximumCoefficientOfVariation(-1.0)
>>> def report_progress(progress):
...     sys.stderr.write('-- progress=' + str(progress) + '%\n')
>>> algo.setProgressCallback(report_progress)
>>> algo.run()

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters:

idint: Internal unique identifier.

setStopCallback(*args)¶

Set up a stop callback.

Can be used to programmatically stop a simulation.

Parameters:

callbackcallable: Returns an int deciding whether to stop or continue.

Examples

Stop a Monte Carlo simulation algorithm using a time limit

>>> import openturns as ot
>>> experiment = ot.MonteCarloExperiment()
>>> X = ot.RandomVector(ot.Normal())
>>> Y = ot.CompositeRandomVector(ot.SymbolicFunction(['X'], ['1.1*X']), X)
>>> event = ot.ThresholdEvent(Y, ot.Less(), -2.0)
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(10000000)
>>> algo.setMaximumCoefficientOfVariation(-1.0)
>>> timer = ot.TimerCallback(0.1)
>>> algo.setStopCallback(timer)
>>> algo.run()