MetaModelValidation¶
- class MetaModelValidation(*args)¶
Base class to score a metamodel and perform validations.
Refer to Cross validation assessment of PC models.
- Parameters:
- inputValidationSample, outputValidationSample2-d sequence of float
The input and output validation samples, not used during the learning step.
- metaModel
Function Metamodel to validate.
Notes
A MetaModelValidation object is used for the validation process of a metamodel. For that purpose, a dataset independent of the learning step, is used to score the surrogate model. Its main functionalities are :
To compute the predictivity factor
To get the residual sample, its non parametric distribution
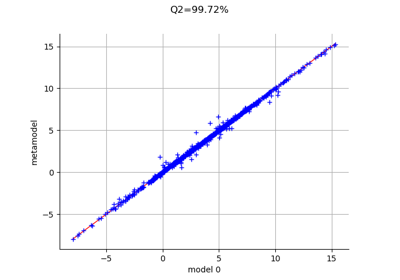
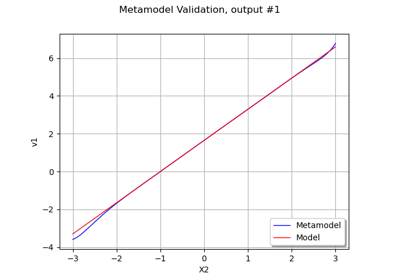
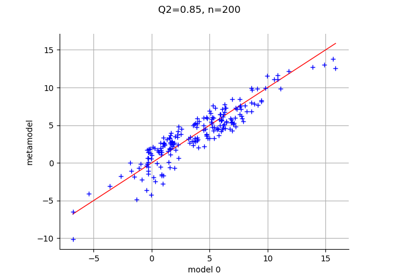
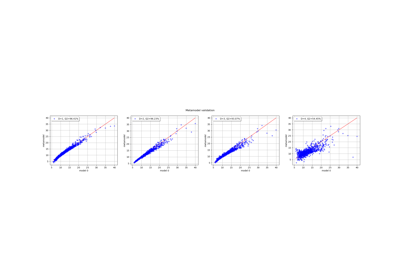
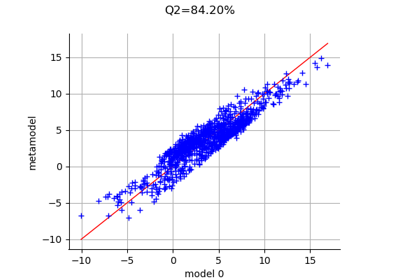
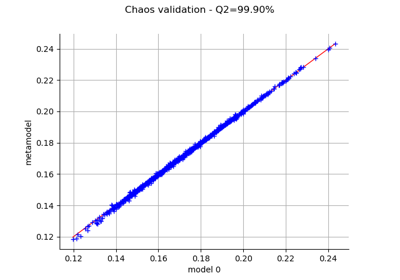
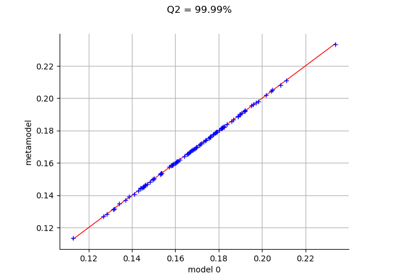
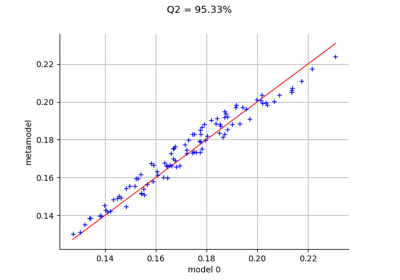
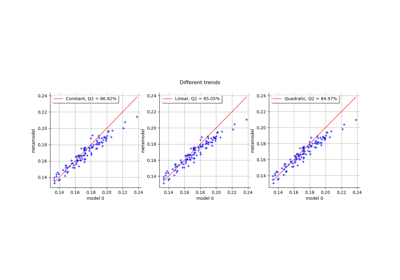
To draw a model vs metamodel validation graph.
Currently only one dimensional output models are available.
Examples
>>> import openturns as ot >>> from math import pi >>> dist = ot.Uniform(-pi/2, pi/2) >>> # Model here is sin(x) >>> model = ot.SymbolicFunction(['x'], ['sin(x)']) >>> # We can build several types of models (kriging, pc, ...) >>> # We use a Taylor developement (order 5) and compare the metamodel with the model >>> metaModel = ot.SymbolicFunction(['x'], ['x - x^3/6.0 + x^5/120.0']) >>> x = dist.getSample(10) >>> y = model(x) >>> # Validation of the model >>> val = ot.MetaModelValidation(x, y, metaModel) >>> # Compute the first indicator : q2 >>> q2 = val.computePredictivityFactor() >>> # Get the residual >>> residual = val.getResidualSample() >>> # Get the histogram of residual >>> histoResidual = val.getResidualDistribution(False) >>> # Draw the validation graph >>> graph = val.drawValidation()
Methods
Compute the predictivity factor.
Plot a model vs metamodel graph for visual validation.
Accessor to the object's name.
getId()Accessor to the object's id.
Accessor to the input sample.
getName()Accessor to the object's name.
Accessor to the output sample.
getResidualDistribution([smooth])Compute the non parametric distribution of the residual sample.
Compute the residual sample.
Accessor to the object's shadowed id.
Accessor to the object's visibility state.
hasName()Test if the object is named.
Test if the object has a distinguishable name.
setName(name)Accessor to the object's name.
setShadowedId(id)Accessor to the object's shadowed id.
setVisibility(visible)Accessor to the object's visibility state.
- __init__(*args)¶
- computePredictivityFactor()¶
Compute the predictivity factor.
- Returns:
- q2
Point The predictivity factor
- q2
Notes
The predictivity factor
is given by :
- drawValidation()¶
Plot a model vs metamodel graph for visual validation.
- Returns:
- graph
GridLayout The visual validation graph.
- graph
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getId()¶
Accessor to the object’s id.
- Returns:
- idint
Internal unique identifier.
- getInputSample()¶
Accessor to the input sample.
- Returns:
- inputSample
Sample Input sample of a model evaluated apart.
- inputSample
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getOutputSample()¶
Accessor to the output sample.
- Returns:
- outputSample
Sample Output sample of a model evaluated apart.
- outputSample
- getResidualDistribution(smooth=True)¶
Compute the non parametric distribution of the residual sample.
- Parameters:
- smoothbool
Tells if distribution is smooth (true) or not. Default argument is true.
- Returns:
- residualDistribution
Distribution The residual distribution.
- residualDistribution
Notes
The residual distribution is built thanks to
KernelSmoothingif smooth argument is true. Otherwise, an histogram distribution is returned, thanks toHistogramFactory.
- getResidualSample()¶
Compute the residual sample.
- Returns:
- residual
Sample The residual sample.
- residual
Notes
The residual sample is given by :
- getShadowedId()¶
Accessor to the object’s shadowed id.
- Returns:
- idint
Internal unique identifier.
- getVisibility()¶
Accessor to the object’s visibility state.
- Returns:
- visiblebool
Visibility flag.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- hasVisibleName()¶
Test if the object has a distinguishable name.
- Returns:
- hasVisibleNamebool
True if the name is not empty and not the default one.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setShadowedId(id)¶
Accessor to the object’s shadowed id.
- Parameters:
- idint
Internal unique identifier.
- setVisibility(visible)¶
Accessor to the object’s visibility state.
- Parameters:
- visiblebool
Visibility flag.
Examples using the class¶
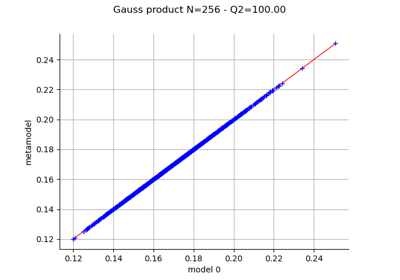
Create a polynomial chaos metamodel by integration on the cantilever beam
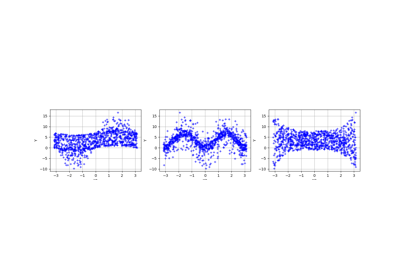
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
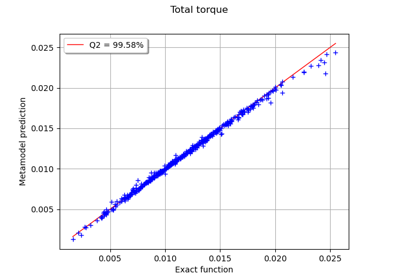
Example of multi output Kriging on the fire satellite model
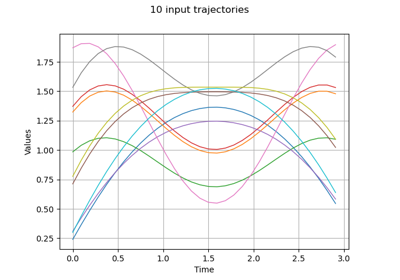
Estimate Sobol indices on a field to point function
 OpenTURNS
OpenTURNS