ScalarCollection¶
- class ScalarCollection(*args)¶
Collection.
Examples
>>> import openturns as ot
Collection of real values:
>>> ot.ScalarCollection(2) [0,0] >>> ot.ScalarCollection(2, 3.25) [3.25,3.25] >>> vector = ot.ScalarCollection([2.0, 1.5, 2.6]) >>> vector [2,1.5,2.6] >>> vector[1] = 4.2 >>> vector [2,4.2,2.6] >>> vector.add(3.8) >>> vector [2,4.2,2.6,3.8]
Collection of complex values:
>>> ot.ComplexCollection(2) [(0,0),(0,0)] >>> ot.ComplexCollection(2, 3+4j) [(3,4),(3,4)] >>> vector = ot.ComplexCollection([2+3j, 1-4j, 3.0]) >>> vector [(2,3),(1,-4),(3,0)] >>> vector[1] = 4+3j >>> vector [(2,3),(4,3),(3,0)] >>> vector.add(5+1j) >>> vector [(2,3),(4,3),(3,0),(5,1)]
Collection of booleans:
>>> ot.BoolCollection(3) [0,0,0] >>> ot.BoolCollection(3, 1) [1,1,1] >>> vector = ot.BoolCollection([0, 1, 0]) >>> vector [0,1,0] >>> vector[1] = 0 >>> vector [0,0,0] >>> vector.add(1) >>> vector [0,0,0,1]
Collection of distributions:
>>> print(ot.DistributionCollection(2)) [Uniform(a = -1, b = 1),Uniform(a = -1, b = 1)] >>> print(ot.DistributionCollection(2, ot.Gamma(2.75, 1.0))) [Gamma(k = 2.75, lambda = 1, gamma = 0),Gamma(k = 2.75, lambda = 1, gamma = 0)] >>> vector = ot.DistributionCollection([ot.Normal(), ot.Uniform()]) >>> print(vector) [Normal(mu = 0, sigma = 1),Uniform(a = -1, b = 1)] >>> vector[1] = ot.Uniform(-0.5, 1) >>> print(vector) [Normal(mu = 0, sigma = 1),Uniform(a = -0.5, b = 1)] >>> vector.add(ot.Gamma(2.75, 1.0)) >>> print(vector) [Normal(mu = 0, sigma = 1),Uniform(a = -0.5, b = 1),Gamma(k = 2.75, lambda = 1, gamma = 0)]
Methods
add(*args)Append a component (in-place).
at(*args)Access to an element of the collection.
clear()Reset the collection to zero dimension.
find(val)Find the index of a given value.
getSize()Get the collection's dimension (or size).
isEmpty()Tell if the collection is empty.
resize(newSize)Change the size of the collection.
select(marginalIndices)Selection from indices.
- __init__(*args)¶
- add(*args)¶
Append a component (in-place).
- Parameters:
- valuetype depends on the type of the collection.
The component to append.
Examples
>>> import openturns as ot >>> x = ot.Point(2) >>> x.add(1.) >>> print(x) [0,0,1]
- at(*args)¶
Access to an element of the collection.
- Parameters:
- indexpositive int
Position of the element to access.
- Returns:
- elementtype depends on the type of the collection
Element of the collection at the position index.
- clear()¶
Reset the collection to zero dimension.
Examples
>>> import openturns as ot >>> x = ot.Point(2) >>> x.clear() >>> x class=Point name=Unnamed dimension=0 values=[]
- find(val)¶
Find the index of a given value.
- Parameters:
- valcollection value type
The value to find
- Returns:
- indexint
The index of the first occurrence of the value, or the size of the container if not found. When several values match, only the first index is returned.
- getSize()¶
Get the collection’s dimension (or size).
- Returns:
- nint
The number of components in the collection.
- isEmpty()¶
Tell if the collection is empty.
- Returns:
- isEmptybool
True if there is no element in the collection.
Examples
>>> import openturns as ot >>> x = ot.Point(2) >>> x.isEmpty() False >>> x.clear() >>> x.isEmpty() True
- resize(newSize)¶
Change the size of the collection.
- Parameters:
- newSizepositive int
New size of the collection.
Notes
If the new size is smaller than the older one, the last elements are thrown away, else the new elements are set to the default value of the element type.
Examples
>>> import openturns as ot >>> x = ot.Point(2, 4) >>> print(x) [4,4] >>> x.resize(1) >>> print(x) [4] >>> x.resize(4) >>> print(x) [4,0,0,0]
- select(marginalIndices)¶
Selection from indices.
- Parameters:
- indicessequence of int
Indices to select
- Returns:
- collsequence
Sub-collection of values at the selection indices.
Examples using the class¶

A quick start guide to the Point and Sample classes
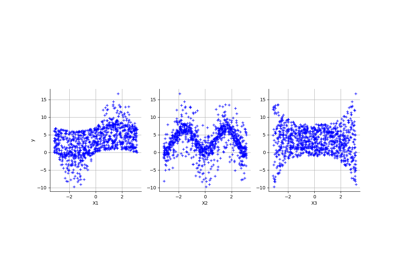
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
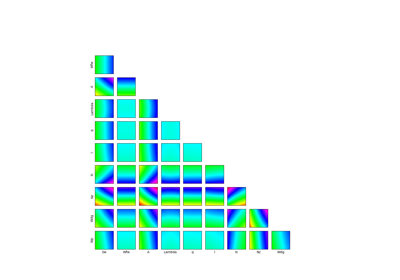
Example of sensitivity analyses on the wing weight model
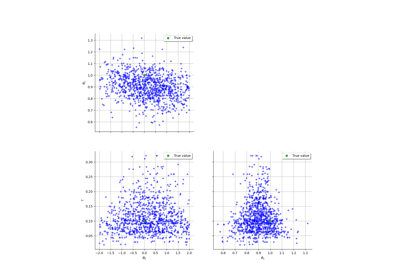
Linear Regression with interval-censored observations
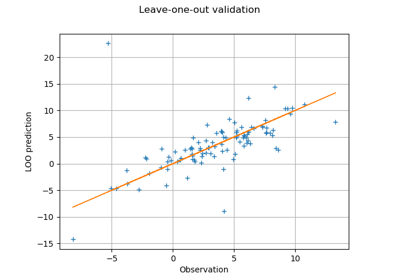
Compute leave-one-out error of a polynomial chaos expansion
 OpenTURNS
OpenTURNS